
思路
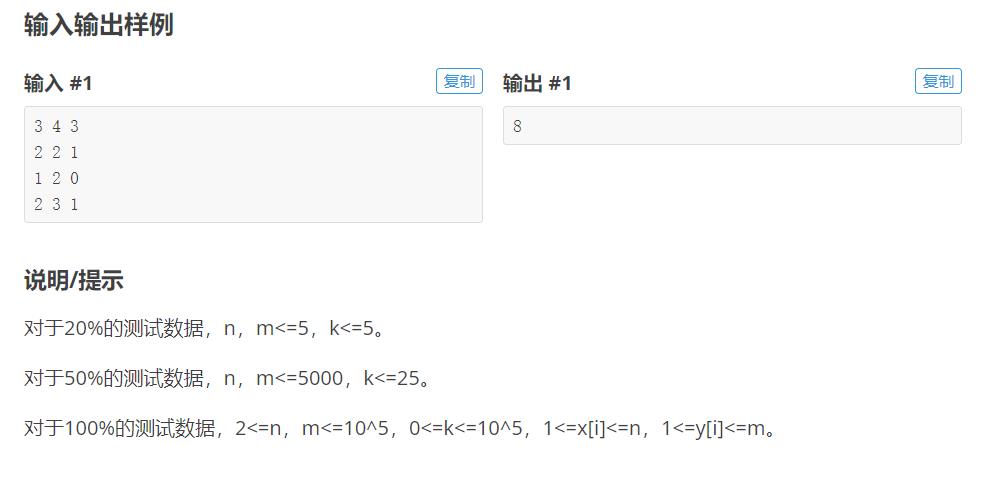
对于这道题,我们从题目里可以知道,蓝色代表的方块为0,红色代表的方块为1。按照题目要求,如果换一种说法,那就是对于一个2*2的方格,其中1的个数必定有奇数个,这样的话,每个方格里的所
有数的异或和必定为1(0^0=0 , 1^0=1 , 11=0)。那么对于每一个格子$a(i,j)$,都有:a(i,j)a(i+1,j)a(i,j+1)a(i+1,j+1)=1
我们钦定S(i , j)为每一个以点(i , j)为右下角的方格的异或和。然后把范围扩大,设想对于一个i*j的方格,它的异或和会是什么呢?(这个部分需要自己推一下,时间关系我就不给例子了)
我们多举几个例子,就可以发现对于任意一个以点(i , j)为右下角的矩阵,它的区域内所有可能的22的方格的异或和再异或起来,得到的就是以(i , j)为右下角的矩阵中包括的所有22矩阵的异
或和的异或和。而这个异或和,根据a^a=0的规定,这个矩阵的S(i , j)仅仅与点(1 , 1)、(i , 1)、(1 , j)、(i , j)有关。
再以此类推,我们就可以发现对于任意一个点,它的值只与(1 , 1)、(i , 1)、(j , 1)这几个点有关。因此我们就可以知道,只要我们明确了表格中第一列和第一行的内容,那表格中其他点
的内容也就是唯一的。
因此,对于a(1 , 1)^a(i , 1)^(1 , j)^a(i , j),当i,j均为偶数时值为1(此时\\((i-1) \\times (j-1)\\)为奇数,对于S函数的异或前缀和为1),否则为0(此时(i-1)*(j-1)为偶数,对于
S函数的异或前缀和为0)。即为a(1 , 1)^a(i , 1)^(1 , j)^a(i , j)=0/1(这里0/1表示值为0或者1)。
这样的话,我们可以考虑枚举a(1 , 1)的值,根据a(i , j)和a(1 , 1)的异同关系(就是对于上一段中说的i , j的奇偶性的问题),就可以确定a(i , 1)和a(1 , j)的异同关系,
即a(i , 1)^a(1 , j)=0/10/1a(i , j)。
那么到现在我们还没有提到过关于并查集的一个字(而这又是一道并查集的题目)。由于我们可以通过枚举a(1 , 1)确定出a(i , 1)和a(j , 1)的异同关系,我们就应该有所启发。
考虑一下食物链那道题。同样都是维护不同的集合,维护集合的关系,这样想这两个题就是极其类似的。我们使用并查集维护有关系的点a(i , 1)和a(j , 1)的异同关系,将他们之间连边。
最后考虑有多少个集合,答案即为2的集合数量减1次方。有人可能会有疑问,为什么不是2的集合个数次方呢?这是因为(1 , 1)这个点自己就是一个集合,但是对答案并没有贡献,所以要减一。
Code
#include<iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 400005
#define MOD 1000000000
typedef long long ll;
int n, m, k;
int f[MAXN], c[MAXN];//c是指该点与其父节点的关系,相同或不同
int ans;
struct node{
int r, c, opt;
} inp[MAXN];//存储读入的信息
inline int read(void){
int f = 1, x = 0;char ch;
do{ch = getchar();if(ch==\'-\')f = -1;} while (ch < \'0\' || ch > \'9\');
do{ x = x * 10 + ch - \'0\';ch = getchar();} while (ch >= \'0\' && ch <= \'9\');
return f * x;
}
inline int get_father(int x) {
if (f[x] == x) return x;
int f1 = get_father(f[x]);
c[x] = c[x] ^ c[f[x]];//这里不要忘了维护该点与父节点的关系
return f[x] = f1;
}
inline int quick_pow(int a,int b){
int res = 1;
while(b){
if(b&1)
res = 1ll * res * a % MOD;
a = 1ll * a * a % MOD;
b >>= 1;
}
return res;
}
inline void calc(int flag) {
for (int i = 1; i <= n + m; ++i)
f[i] = i, c[i] = 0;//初始化要到n+m,因为维护的是第一行和第一列的点,共n+m个
if (flag == 1){//如果点(1,1)是1,那么对除该点外所有数处理(详见题解里推的式子)
for (int i = 1; i <= k; ++i) {
if (inp[i].r > 1 && inp[i].c > 1)
inp[i].opt ^= 1;//0^1=1,1^1=0,0^0=0
}
}
f[n + 1] = 1;//我们把第一列的数从1到m编号,把第一行的点从n+1到n+n编号,那么(1,1)点的编号会有1和n+1两个,这里直接连边
for (int i = 1; i <= k; ++i) {//枚举每一个给定的点
if (inp[i].r == 1 && inp[i].c == 1)
continue;//如果是(1,1),忽略即可
int f1 = get_father(inp[i].r), f2 = get_father(inp[i].c + n);//取父亲
if (f1 == f2) {//如果已经在同一集合里了,则判断是否满足关系式
if ((c[inp[i].r] ^ c[inp[i].c + n]) != inp[i].opt)
return;//不满足直接返回
}
else {
f[f1] = f2;//如果不在同一集合,那么连边
c[f1] = c[inp[i].c + n] ^ c[inp[i].r] ^ inp[i].opt;//更新异同关系
}
}
int cnt = 0;
for (int i = 1; i <= n + m;++i)
if(f[i]==i)++cnt;
ans = (1ll * ans + quick_pow(2, cnt - 1)) % MOD;
}
int main() {
n = read(), m = read();
k = read();
int ck = -1;
for (int i = 1; i <= k; ++i) {
inp[i].r = read(), inp[i].c = read();
inp[i].opt = read();
if ((!(inp[i].r & 1)) && (!(inp[i].c & 1)))
inp[i].opt ^= 1;//如果i,j同是偶数,异或1
if (inp[i].r == 1 && inp[i].c == 1)
ck = inp[i].opt;//若给定了(1,1)的值,存储下来
}
if (ck == -1 || ck == 0) calc(0);//枚举
if (ck == -1 || ck == 1) calc(1);
printf("%lld\\n", ans);//输出
return 0;
}