LeetCode91. 解码方法

Posted 2020-12-17 machine_gun_lin

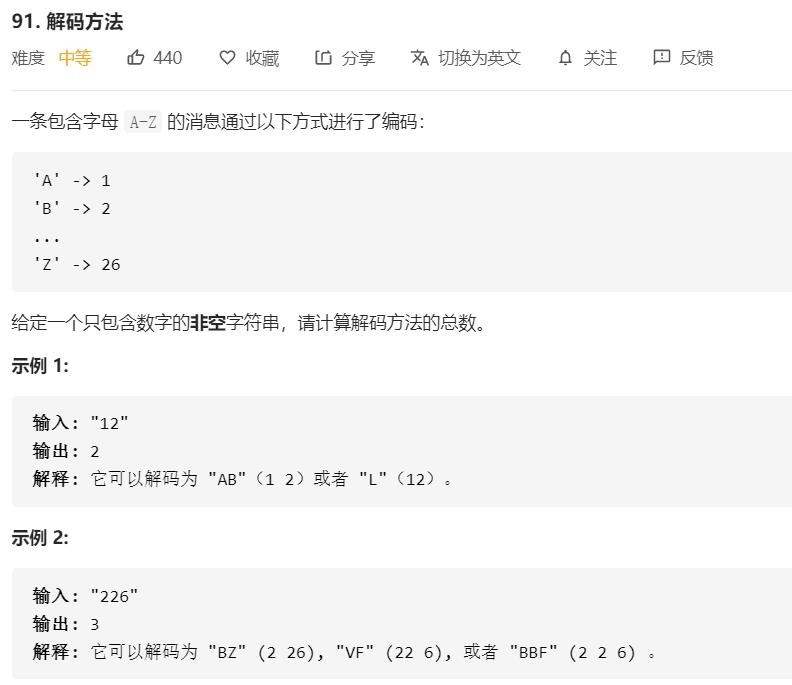
经典dp问题，用dp[i]表示前i个字符解码方案的总数。

显然dp[0]=1（空字符也相当于一种解码方案），
然后从小到大递推计算dp数组，如果当前当前数字不是0（也就是大于等于1小于等于9），则当前字符可以连接在之前所有字符之后成为一个新方案。
当前字符是0是不行的，0不能映射成英文字母。
所以有：

if(\'1\' <= s[i] && s[i] <= \'9\') {
      dp[i] = dp[i - 1];
}

不过还是有一种情况，就是当前字符和前一个字符的结合combination可以映射为一个别的字母，比如前一个字母是2，当前字母是6，则combination可以解码为26.

所以要判断当前字母和前一个字母的combination是否大于等于10且小于等于26. 如果是，则前i个字母的解码方案还要再加上前i-2个字母的解码方案：

int combination = (s[i - 1] - \'0\') * 10 + (s[i] - \'0\');
if(10 <= combination && combination <= 26) {
      dp[i] += dp[i - 2];
}

最后，我们需要知道字符串s的解码方案，返回dp[size]即可。

完整代码：

class Solution {
public:
    int numDecodings(string s) {
        int size = s.size();
        vector<int> dp(size + 1);
        s = \' \' + s;
        dp[0] = 1;
        for(int i = 1; i <= size; ++i) {
            if(\'1\' <= s[i] && s[i] <= \'9\') {
                dp[i] = dp[i - 1];
            }
            if(i >= 2) {
                int combination = (s[i - 1] - \'0\') * 10 + (s[i] - \'0\');
                if(10 <= combination && combination <= 26) {
                    dp[i] += dp[i - 2];
                }
            }
        }
        return dp[size];
    } 
};