今日得到: 位运算真的是 666, 计算机基础还有数学知识都很重要.
LeetCode-191 二进制位1的个数
LeetCode上第 191 号问题:编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数。
观察一下 n 与 n-1 这两个数的二进制表示:对于 n-1 这个数的二进制来说,相对于 n 的二进制,它的最末位的一个 1 会变成 0,最末位一个 1 之后的 0 会全部变成 1,其它位相同不变。
比如 n = 8888,其二进制为 10001010111000
则 n - 1 = 8887 ,其二进制为 10001010110111
通过按位与操作后:n & (n-1) = 10001010110000
也就是说:通过 n&(n-1)这个操作,可以起到消除最后一个1的作用。
所以可以通过执行 n&(n-1) 操作来消除 n 末尾的 1 ,消除了多少次,就说明有多少个 1 。
class Solution:
def hammingWeight(self, n):
res = 0
while n != 0:
res += 1
n &= (n - 1)
return res
def hammingWeight2(self, n):
res = 0
while n != 0:
res += (n & 1)
n = n >> 1
return res
LeetCode-231 2的幂
给定一个整数,编写一个函数来判断它是否是 2 的幂次方。

仔细观察,可以看出 2 的次方数都只有一个 1 ,剩下的都是 0 。根据这个特点,只需要每次判断最低位是否为 1 ,然后向右移位,最后统计 1 的个数即可判断是否是 2 的次方数, 可以使用上一个问题的解法
def isPowerOfTwo(n):
res = 0
while n != 0:
res += (n & 1)
n >>= 1
return res == 1
该题还有一种巧妙的解法。再观察上面的表格,如果一个数是 2 的次方数的话,那么它的二进数必然是最高位为1,其它都为 0 ,那么如果此时我们减 1 的话,则最高位会降一位,其余为 0 的位现在都为变为 1,那么我们把两数相与,就会得到 0.

比如 2 的 3 次方为 8,二进制位 1000 ,那么 8 - 1 = 7,其中 7 的二进制位 0111
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return (n > 0) and ((n & (n - 1)) == 0)
LeetCode-201. 闭区间范围内数字按位与
给定范围 [m, n],其中 0 <= m <= n <= 2147483647,返回此范围内所有数字的按位与(包含 m, n 两端点)
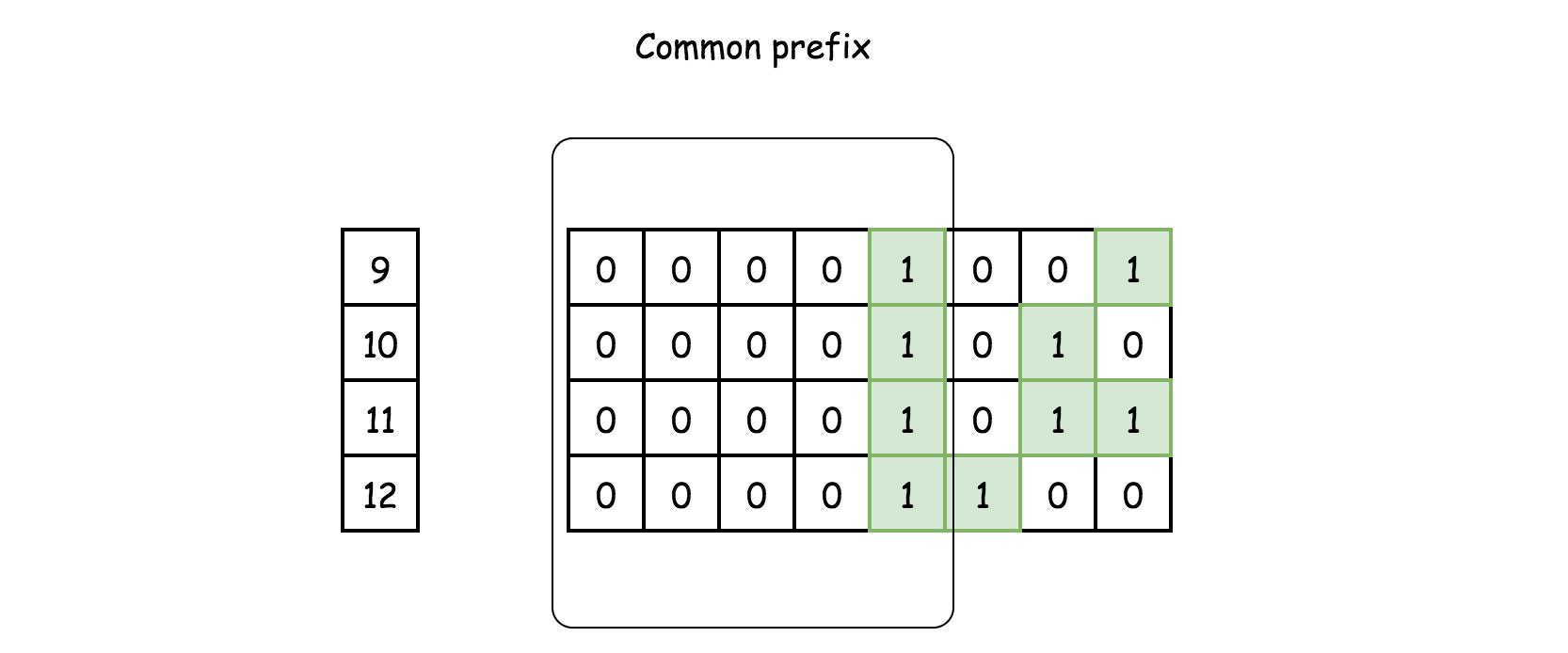
所有这些位字符串的公共前缀也是指定范围的起始和结束编号的公共前缀(即在上面的示例中分别为 9 和 12),因此,我们可以将问题重新表述为:给定两个整数,要求我们找到她们二进制字符串的公共前缀
- 使用191的方法
Brian Kernighan 算法n & (n-1)
class Solution:
def rangeBitwiseAnd(self, m: int, n: int) -> int:
while m < n:
# turn off rightmost 1-bit
n = n & (n - 1)
return m & n
- 找m, n 的最高位1出现的位置 , 如果不相等,则返回0,如果相等,则找公共前缀。B站视频-位运算练习【LeetCode】
LeetCode-187.重复的DNA序列
所有 DNA 都由一系列缩写为 A,C,G 和 T 的核苷酸组成,例如:“ACGAATTCCG”。在研究 DNA 时,识别 DNA 中的重复序列有时会对研究非常有帮助。
编写一个函数来查找目标子串,目标子串的长度为 10,且在 DNA 字符串 s 中出现次数超过一次。差点没看懂题 QAQ!
输入:s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出:["AAAAACCCCC", "CCCCCAAAAA"]
# 普通解法
class Solution:
def findRepeatedDnaSequences(self, s: str) -> List[str]:
d = {}
for i in range(len(s) - 9):
k = s[i: i+10]
if k in d:
d[k] = True
else:
d[k] = False
return [*filter(lambda x: d[x], d)]
该的位运算解法暂时没看懂,先记录着,有点晕了,后面继续看
LeetCode-36.只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
要求: 你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
输入: [2,2,1] 输出: 1 输入: [4,1,2,1,2] 输出: 4
这题比较简单,想到异或运算,相同为0,不同为1的规则就可以很快求解了
| a | b | a⊕b |
|---|---|---|
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
class Solution:
def singleNumber(self, nums: List[int]) -> int:
# 非空数组暂时不用判断
from functools import reduce
return reduce(lambda a, b: a ^ b, nums)
LeetCode-137.只出现一次的数字 II
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
要求: 你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
输入: [2,2,3,2] 输出: 3 输入: [0,1,0,1,0,1,99] 输出: 99
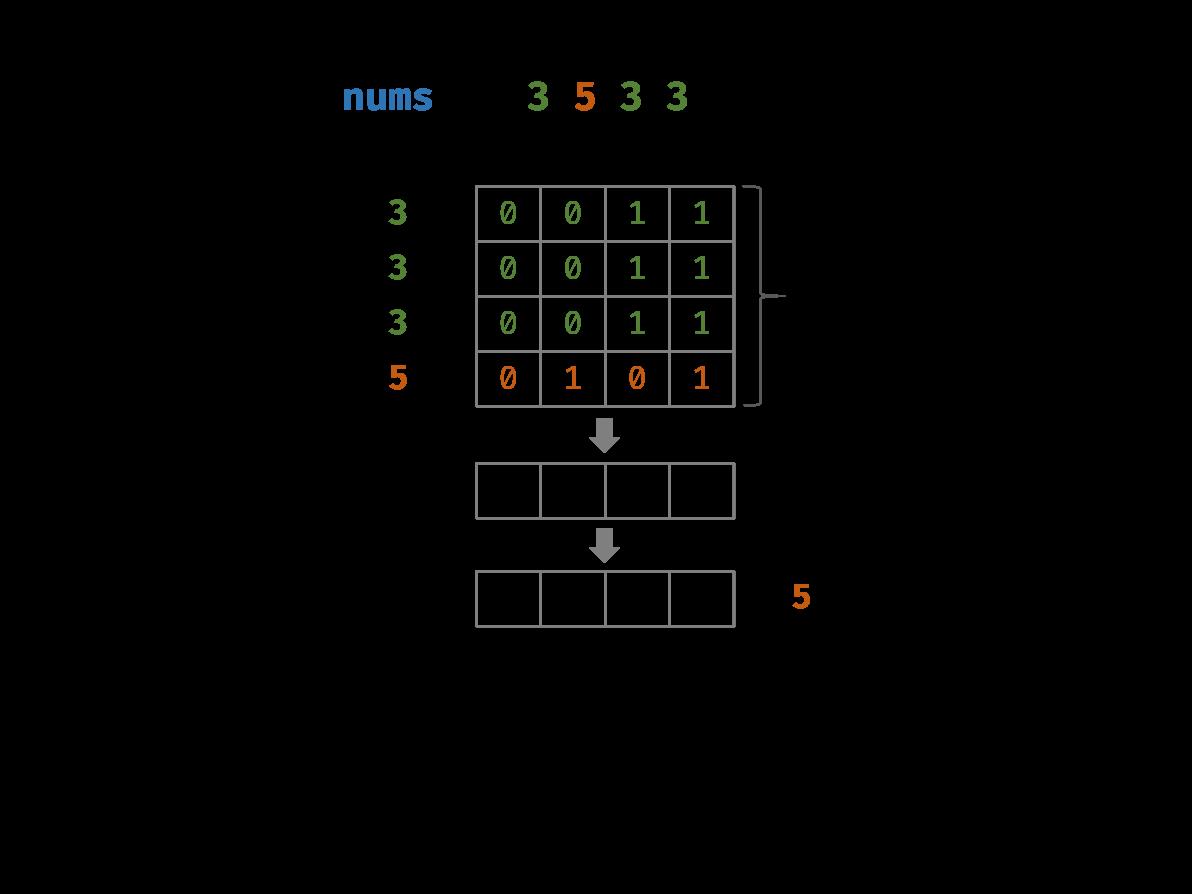
3×(a+b+c)−(a+a+a+b+b+b+c)=2c 也可以应用在上一题
## 普通解法
class Solution:
def singleNumber(self, nums):
return (3 * sum(set(nums)) - sum(nums)) // 2
推广到一般情况:
如果其他数都出现了 k 次,一个数出现了一次。那么如果 k 是偶数,还是把所有的数异或起来就行了。如果 k 是奇数,那么统计每一位是 1 的个数,然后模 k 取余数就能得到那个单独的数了 。其中有
sum = kn + 1
位运算的解法是有限状态机+位运算,感觉有点难理解,自己推敲一遍勉强可以理解,自己画一个状态表,然后推导出响应的公式就比较好了。
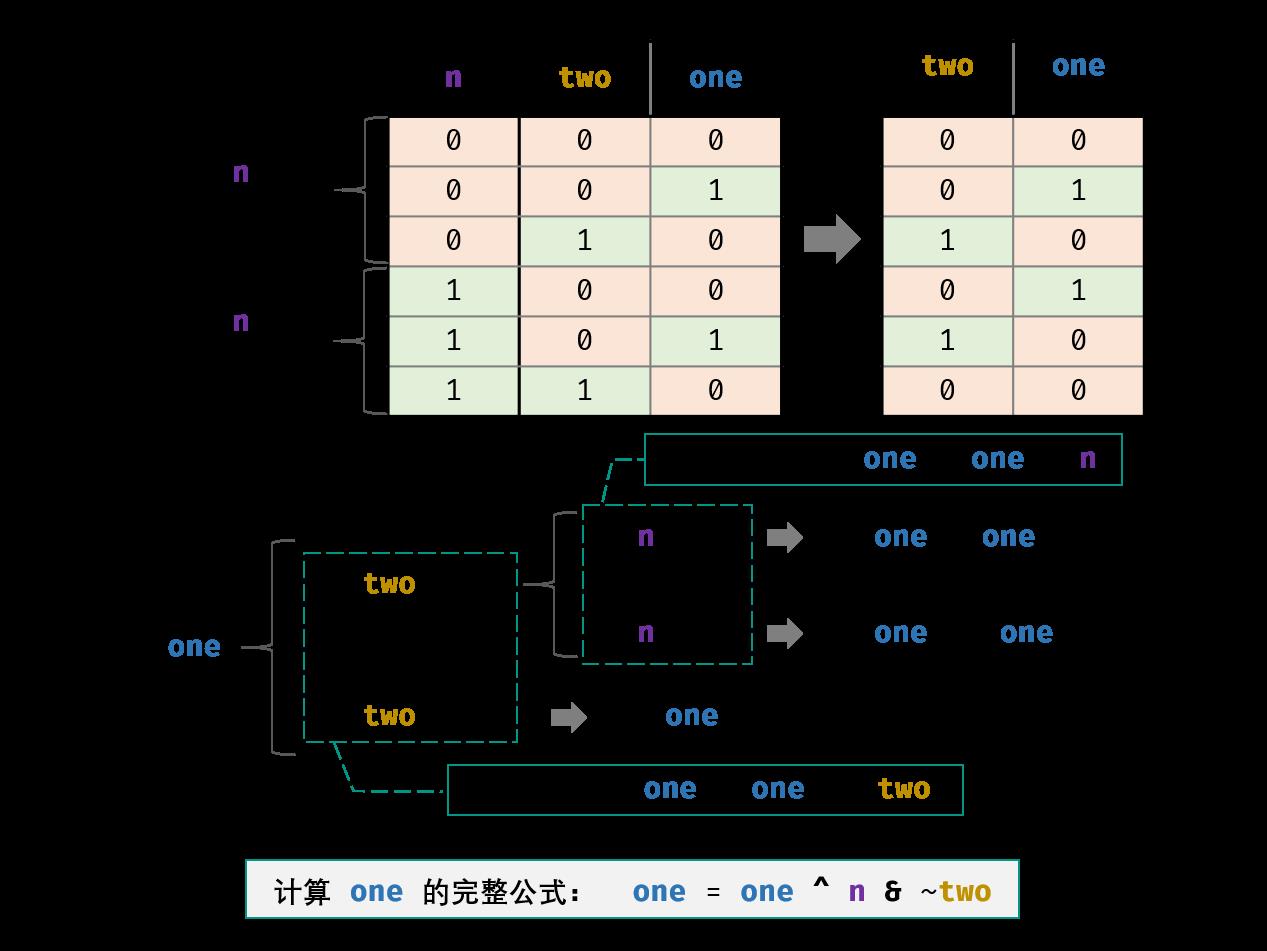
我是先看题解1, 在看题解2,才搞明白了。
几乎每道题都能看到题解2的作者,佩服不已,时而习之,但求甚解。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ones, twos = 0, 0
for num in nums:
ones = ones ^ num & ~twos
twos = twos ^ num & ~ones
return ones
LeetCode-260. 只出现一次的数字 III
给定一个整数数组
nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。输入: [1,2,1,3,2,5] 输出: [3,5]
注意:
- 结果输出的顺序并不重要,对于上面的例子,
[5, 3]也是正确答案。 - 你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
根据前面找一个不同数的思路算法,在这里把所有元素都异或,那么得到的结果就是那两个只出现一次的元素异或的结果。
如果我们把原数组分成两组,只出现过一次的两个数字分别在两组里边,那么问题就转换成之前的老问题了,只需要这两组里的数字各自异或,答案就出来了。
那么通过什么把数组分成两组呢?
放眼到二进制,我们要找的这两个数字是不同的,所以它俩至少有一位是不同的,所以我们可以根据这一位,把数组分成这一位都是 1 的一类和这一位都是 0 的一类,这样就把这两个数分到两组里了。
那么怎么知道那两个数字哪一位不同呢?
回到我们异或的结果,如果把数组中的所有数字异或,最后异或的结果,其实就是我们要找的两个数字的异或。而异或结果如果某一位是 1,也就意味着当前位两个数字一个是 1 ,一个是 0,也就找到了不同的一位。
以上思路源于作者:windliang
class Solution:
def FindNumsAppearOnce(self, nums):
length = len(nums)
if length <= 0:
return nums
result = 0
# 先将所有数子异或得到一个值
for num in nums:
result ^= num
# 找到这个值最低位二进制位1的位置,根据这个位置来区分两个数组,分别异或求出只出现一次的数字
firstBitIndex = self.FindFirstBit(result)
n1, n2 = 0, 0
for num in nums:
if self.IsSameBit(num, firstBitIndex):
n1 ^= num
else:
n2 ^= num
return n1, n2
def FindFirstBit(self, num):
indexBit = 0
while num & 1 == 0:
indexBit += 1
num = num >> 1
return indexBit
def IsSameBit(self, num, indexBit):
num = num >> indexBit
return num & 1
# 解放2
class Solution2:
def FindNumsAppearOnce(self, nums):
length = len(nums)
if length <= 0:
return []
diff = 0
for i in nums:
diff ^= i
n1, n2 = 0, 0
minDiff = self.getMinDiff(diff)
for num in nums:
if minDiff & num == 0:
n1 ^= num
n2 = diff ^ n1
return n1, n2
def getMinDiff(self, num):
# 保留一个低位是1的数字
# 取负号其实就是先取反,再加 1,需要 补码 的知识。最后再和原数相与就会保留最低位的 1。比如 1010,先取反是 0101,再加 1,就是 0110,再和 1010 相与,就是 0010 了
return num & (-num)
如何得到二进制位只有一个1的数,几种方法
diff &= -diff ; 这里 的做法。
取负号其实就是先取反,再加 1,需要 补码 的知识。最后再和原数相与就会保留最低位的 1。比如 1010,先取反是 0101,再加 1,就是 0110,再和 1010 相与,就是 0010 了。
diff = (diff & (diff - 1)) ^ diff; 这里 的做法
n & (n - 1) 的操作在 191 题 用过,它可以将最低位的 1 置为 0。比如 1110,先将最低位的 1 置为 0 就变成 1100,然后再和原数 1110 异或,就得到了 0010
diff = xor & ~(diff - 1) 这里 的做法
先减 1,再取反,再相与。比如 1010 减 1 就是 1001,然后取反 0110,然后和原数 1010 相与,就是 0010 了
mask=1
while((diff & mask)==0):
mask <<= 1
# mask 就是我们要构造的了
这里 的做法
推到1到N连续自然数的异或值
| 1 | 1=1; | 1 |
|---|---|---|
| 2 | 1^2=3; | n+1 |
| 3 | 123=0; | 0 |
| 4 | 123^4=4; | n |
| 5 | 12345=1; | 1 |
| 6 | 12345^6=7; | n+1 |
| 7 | 1234567=0; | 0 |
| 8 | 1234567^8=8; | n |
| ... | ... | ... |
四个数一次循环:1, n+1, 0, n
def main(n):
k = n % 4
res = {
0: n,
1: 1,
2: n + 1,
3: 0
}
return res[k]
例题1:给你一个n,求出123....n的值 数据范围: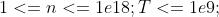
例题2: 求[m, n]之间的连续异或的值
# 根据异或的性质推到可以得到如下结果,则有化简为1->n之间的异或
f([m, n]) = f([1, n])^f([1, m-1])
参考资料
补码为什么按位取反再加一认真看完会有收获的。