题目描述
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
示例:
输入: 4->2->1->3
输出: 1->2->3->4
题目链接: https://leetcode-cn.com/problems/sort-list/
思路1
使用两个栈来做,类似于栈排序的方法。代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head==nullptr) return head;
stack<ListNode*> s;
stack<ListNode*> help; // 辅助栈
ListNode* cur = head;
while(cur!=nullptr){
if(s.empty()) s.push(cur);
else{
while(!s.empty() && cur->val>s.top()->val){
help.push(s.top()); s.pop();
}
s.push(cur);
while(!help.empty()){
s.push(help.top()); help.pop();
}
}
cur = cur->next;
}
ListNode* dummy = new ListNode(0);
cur = dummy;
while(!s.empty()){
ListNode* node = s.top(); s.pop();
node->next = nullptr;
cur->next = node;
cur = cur->next;
}
return dummy->next;
}
};
// 超时
这种方不满足 O(n log n) 时间复杂度和常数级空间复杂度,并且会超时。
思路2
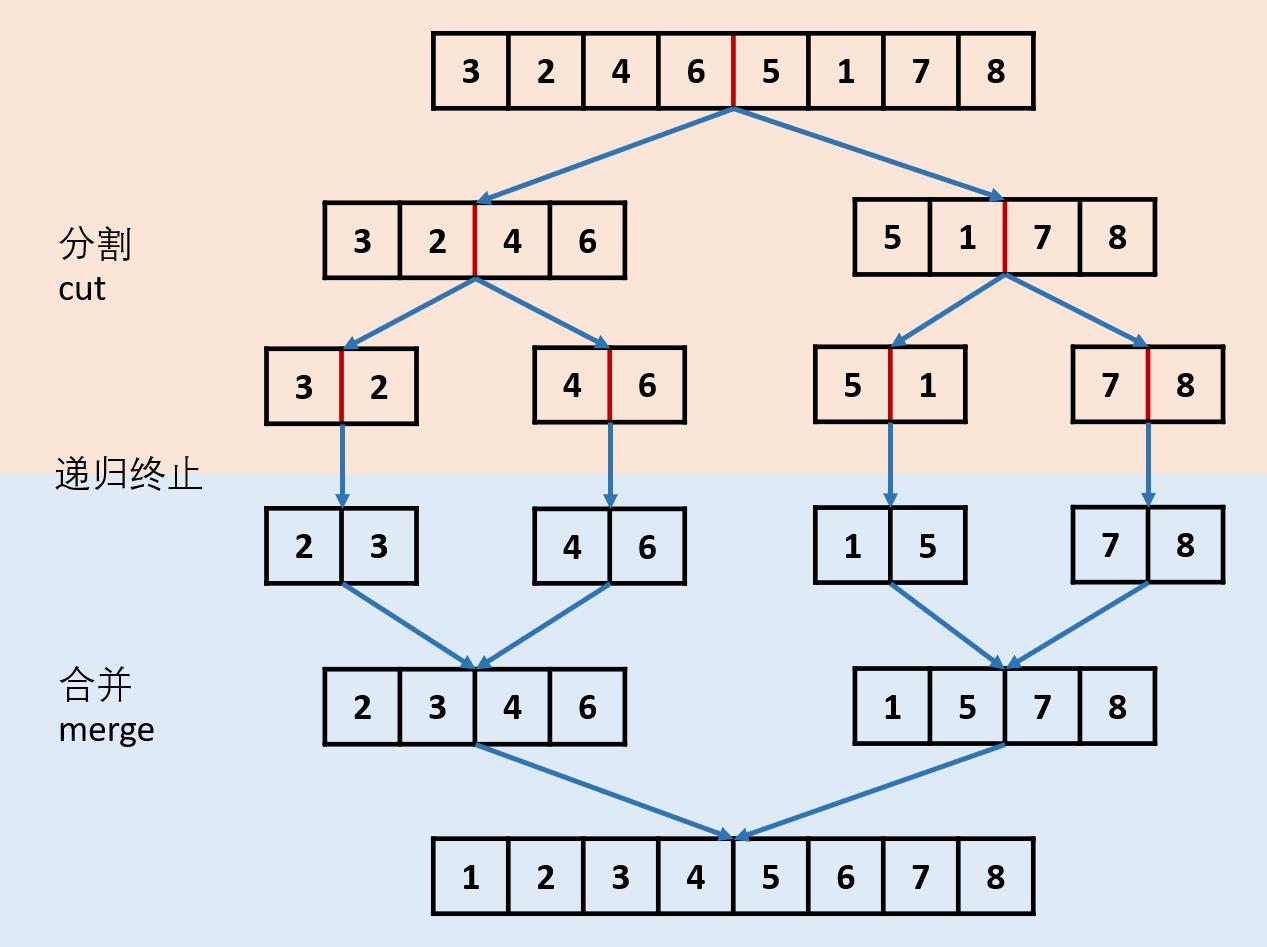
使用归并排序。
先划分,当前节点为空或者当前节点的下一个节点为空就返回合并。在分割的时候需要找到链表的中点分割。如果链表长度是奇数,则只有唯一的中点;如果链表长度是偶数,则有两个中点,需要使用左边的中点,具体可参考链表的中间节点。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head==nullptr || head->next==nullptr) return head; // 注意条件的后半部分
ListNode* slow = head;
ListNode* fast = head;
while(fast->next!=nullptr && fast->next->next!=nullptr){ // 注意:链表长度为偶数,使用左边的中点
fast = fast->next->next;
slow = slow->next;
}
ListNode* temp = slow->next;
slow->next = nullptr;
ListNode* left = sortList(head);
ListNode* right = sortList(temp);
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
while(left!=nullptr && right!=nullptr){
if(left->val<right->val){
cur->next = left;
left = left->next;
}else{
cur->next = right;
right = right->next;
}
cur = cur->next;
}
cur->next = (left==nullptr? right:left);
return dummy->next;
}
};
这样写也行:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
return mergeSort(head, NULL);
}
ListNode* mergeSort(ListNode* left, ListNode* right){
if(left==NULL || left->next==NULL) return left; // 注意返回条件
ListNode* slow = left;
ListNode* fast = left;
while(fast->next!=right && fast->next->next!=right){
slow = slow->next;
fast = fast->next->next;
}
ListNode* next = slow->next;
slow->next = NULL;
ListNode* list1 = mergeSort(left, slow);
ListNode* list2 = mergeSort(next, right);
return mergeTwoLists(list1, list2);
}
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){
if(list1==NULL) return list2;
if(list2==NULL) return list1;
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
while(list1!=NULL && list2!=NULL){
if(list1->val<list2->val){
cur->next = list1;
list1 = list1->next;
}else{
cur->next = list2;
list2 = list2->next;
}
cur = cur->next;
}
if(list1!=NULL) cur->next = list1;
if(list2!=NULL) cur->next = list2;
return dummy->next;
}
};
这样写可以和(有序链表转换二叉搜索树)[https://www.cnblogs.com/flix/p/13307886.html]统一起来。
- 时间复杂度:O(nlogn)
- 空间复杂度:O(logn)
思路3
使用快速排序。
对于数组的快排算法,核心是进行划分 (partition),确定一个轴点,将小于等轴点的数调整在轴点之前,将大于等于轴点的数调到轴点之后,然后返回轴点的下标。在划分算法中,需要分别从数组的前面和后面对数组进行遍历,后面的下标向前移动。但是在单链表中,并没有向前的指针,无法向链表前面移动。 确定第一个元素的轴点 定义两个指针,fast 和 slow。(目标是在从头到 slow 之间的元素均小于等于轴点;slow 到 fast 之间的元素均大于等于轴点); fast 向后移动,如果 fast < pivot,则 slow 先后移,然后交换 slow 和 fast 的值。这样可以保证 slow 永远是最后一个小于等于 pivot 的元素,而 slow 的下一个是大于等于 pivot 的元素。
代码如下:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
quickSort(head, NULL);
return head;
}
void quickSort(ListNode* head, ListNode* tail){
if(head==NULL || head==tail) return;
ListNode* pivot = partition(head, tail);
quickSort(head, pivot);
quickSort(pivot->next, tail);
}
ListNode* partition(ListNode* begin, ListNode* end){
if(begin==end) return begin;
ListNode* slow = begin;
ListNode* fast = begin->next;
while(fast!=end){
if(fast->val < begin->val){
slow = slow->next;
swap(fast->val, slow->val);
}
fast = fast->next;
}
swap(begin->val, slow->val);
return slow;
}
};
- 时间复杂度:O(nlogn)
- 空间复杂度:O(logn)