求所有不重复路径, Unique Paths， LeetCode题解

Posted 2020-12-13 import_SOBER

---

求所有不重复的路径问题

A robot is located at the top-left corner of a m x n grid (marked \'Start\' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked \'Finish\' in the diagram below).

How many possible unique paths are there?

Above is a 7 x 3 grid. How many possible unique paths are there?

 

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

 

Constraints:

• 1 <= m, n <= 100
• It\'s guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

---

递归解法

求所有不相同的路径，从左上角走到右下角。走法只能是向下或者向右。

题目中给示例是3 X 2的输入，就是两行三列，走法共3种。

容易看出，所有的步骤可以用一个二叉树存储。例如

1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

画成二叉树就是：

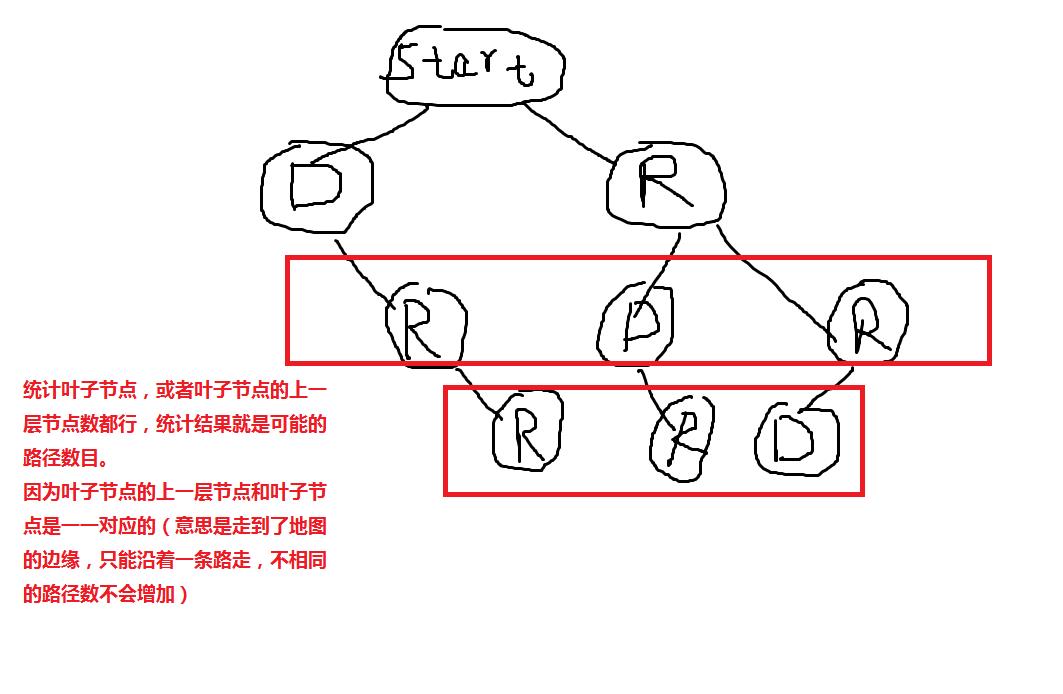
  所以问题转化为构建二叉树和统计二叉树叶子节点个数的问题。

class Node:
    def __init__(self, left=None, right=None):
        self.left = left
        self.right = right

class Solution(object):
    def uniquePaths(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        def recursive(m, n):
            root = Node()
            if m == 1 and n == 1:
                return None
            elif m > 1 and n > 1:
                root.right = recursive(m-1, n)
                root.left = recursive(m, n-1)
            elif m > 1:
                root.right = recursive(m - 1, n)
            elif n > 1:
                root.left = recursive(m, n-1)
            return root

        def count_leaves(root):
            count = 0
            if root.left is None and root.right is None:
                count += 1
            if root.left is not None:
                count += count_leaves(root.left)
            if root.right is not None:
                count += count_leaves(root.right)
            return count
        root = recursive(m, n)
        if not root:
            return 1
        return count_leaves(root)


a = Solution()
b = a.uniquePaths(1, 1)
print(b)

不过很遗憾，这种算法leetcode OJ跑到 37 / 62 个测试样例时就超时了。可以尝试在这个想法上进行改进，比如不建二叉树，直接在m=1和n=1时进行计数+1。但由于是递归，重复计算太多。

m行n列的数据，时间复杂度是O(m!)*O(n!)

 

    def uniquePaths2(self, m, n):
        """
        :type m: int
        :type n: int
        :rtype: int
        """
        def recursive(m, n):
            count = 0
            if m == 1 and n == 1:
                count = 1
            elif m > 1 and n > 1:
                count = recursive(m - 1, n) + recursive(m, n - 1)
            elif m > 1:
                count = recursive(m - 1, n)
            elif n > 1:
                count = recursive(m, n - 1)
            return count

        count = recursive(m, n)
        return count

　　

---

 

 

 动态规划解法　

然而如果画出一张二维表，表中每个点表示，到当前位置的所有路径数，问题就可用成动态规划求解，时间、空间复杂度均O（m*n）

 

 

 

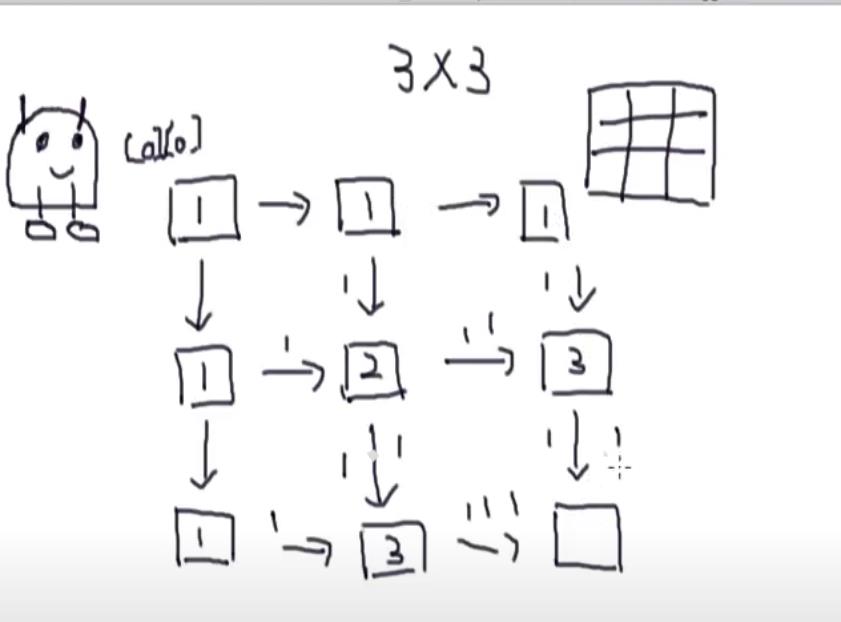
class Solution(object):
    def uniquePaths(self, m, n):
        road_map = [[1]*m]*n
        for i in range(1, n):
            for j in range(1, m):
                road_map[i][j] = road_map[i-1][j] + road_map[i][j-1]
        return road_map[n-1][m-1]

　　

---

 

换硬币问题，给定零钱集合与固定金额，求有多少种换零钱的方法

Example 1:

Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

Input: amount = 10, coins = [10] 
Output: 1

 同样，这个问题是类似的，也可以用递归方法求解。

为什么用递归？因为首先想到的是缩减问题规模，本来5块钱，用了一个1块钱的硬币，那么就剩下4块钱了，问题规模也就缩减至4块钱换零钱的问题。

但是递归就意味着重复计算，时间复杂度太高，只能解决超小规模问题（稍微大点就不行了）。

那么还是需要用动态规划求解。

动态规划相当于（1）问题规模缩小+（2）寻找子问题，这两个都考虑到并转化为公式，还是有一定难度（思想上）。

思路（对于示例中的问题，金额=5，零钱集=[1, 2, 5]）：

（1）零钱集为空[]，那么对任何金额都无解，即换零钱的方法为0种；

（2）金额为0时，对于任何零钱集，换零钱的方法都是一种，即不给任何硬币，就能完成问题；

（3）零钱集逐次增加一种类型的硬币；

（4）金额的粒度为整数1，因此可以让金额从0开始每次+1，一直增长到金额5.

（5）画出矩阵，矩阵中元素含义为：使用当前的零钱集，有多少种方法换到当前的金额？

（6）矩阵中元素的计算：

我是否应该使用零钱集中新加入的那种类型的硬币？如果我不使用，那么我相当于使用的是上一步（上一行）中的零钱集来求解当前位置的金额的换硬币方法，而这个方法已经计算出来了，就在当前元素的上一行正上方。

如果我使用了零钱集中新加入的那种类型的硬币一次，假如新加入的那种类型的硬币面值x，当前的金额是y，由于我使用了x，那么金额就会变成y-x。所以如果我知道当金额是y-x时，使用当前的零钱集有多少种换法，就知道了问题的解。这里相当于在矩阵当前元素的同一行的左边（因为金额减少了,y-x<y）去寻找答案。

 

class Solution(object):
    def change(self, amount, coins):
        """
        :type amount: int
        :type coins: List[int]
        :rtype: int
        """
        sub_problem_table = [[0 for i in range(amount + 1)] for j in range(len(coins) + 1)]
        sub_problem_table[0][0] = 1  # 相当于0元用空零钱集[]去换，共有1种换法
        for row_id in range(1, len(coins) + 1):
            sub_problem_table[row_id][0] = 1  # 相当于0元钱用各种硬币换，换法只有一种那就是什么也不换

        for coins_type in range(1, len(coins) + 1):
            for money in range(1, amount + 1):
                not_using_ways = sub_problem_table[coins_type - 1][money]
                if coins[coins_type - 1] > money:
                    using_ways = 0
                else:
                    using_ways = sub_problem_table[coins_type][money - coins[coins_type - 1]]
                sub_problem_table[coins_type][money] = not_using_ways + using_ways
        return sub_problem_table[-1][-1]