leetcode题解之42. 接雨水

Posted 2020-12-13 刷题之路1

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

https://www.jianshu.com/p/6d1422540768

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

??视频题解

刷新重试诊断

code：

vid:

uuid:

requestId:

播放时间：

提示信息

字幕

倍速

清晰度

音轨

倍速正常

字幕Off

音轨

清晰度

00:00 / 19:43

确认取消

??文字题解

方法 1：暴力

直观想法

直接按问题描述进行。对于数组中的每个元素，我们找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。

算法

• 初始化 $ans=0$
• 从左向右扫描数组：
  • 初始化 $ext{max\_left}=0$ 和 $ext{max\_right}=0$
  • 从当前元素向左扫描并更新：
    • $ext{max\_left}=max( ext{max\_left}, ext{height}[j])$
  • 从当前元素向右扫描并更新：
    • $ext{max\_right}=max( ext{max\_right}, ext{height}[j])$
  • 将$min( ext{max\_left}, ext{max\_right}) - ext{height}[i]$ 累加到 $ext{ans}$

• C++

int trap(vector<int>& height)
{
    int ans = 0;
    int size = height.size();
    for (int i = 1; i < size - 1; i++) {
        int max_left = 0, max_right = 0;
        for (int j = i; j >= 0; j--) { //Search the left part for max bar size
            max_left = max(max_left, height[j]);
        }
        for (int j = i; j < size; j++) { //Search the right part for max bar size
            max_right = max(max_right, height[j]);
        }
        ans += min(max_left, max_right) - height[i];
    }
    return ans;
}

复杂性分析

• 时间复杂度： $O(n^2)$。数组中的每个元素都需要向左向右扫描。

• 空间复杂度 $O(1)$ 的额外空间。
  
  
  
  

---

方法 2：动态编程

直观想法

在暴力方法中，我们仅仅为了找到最大值每次都要向左和向右扫描一次。但是我们可以提前存储这个值。因此，可以通过动态编程解决。

这个概念可以见下图解释：

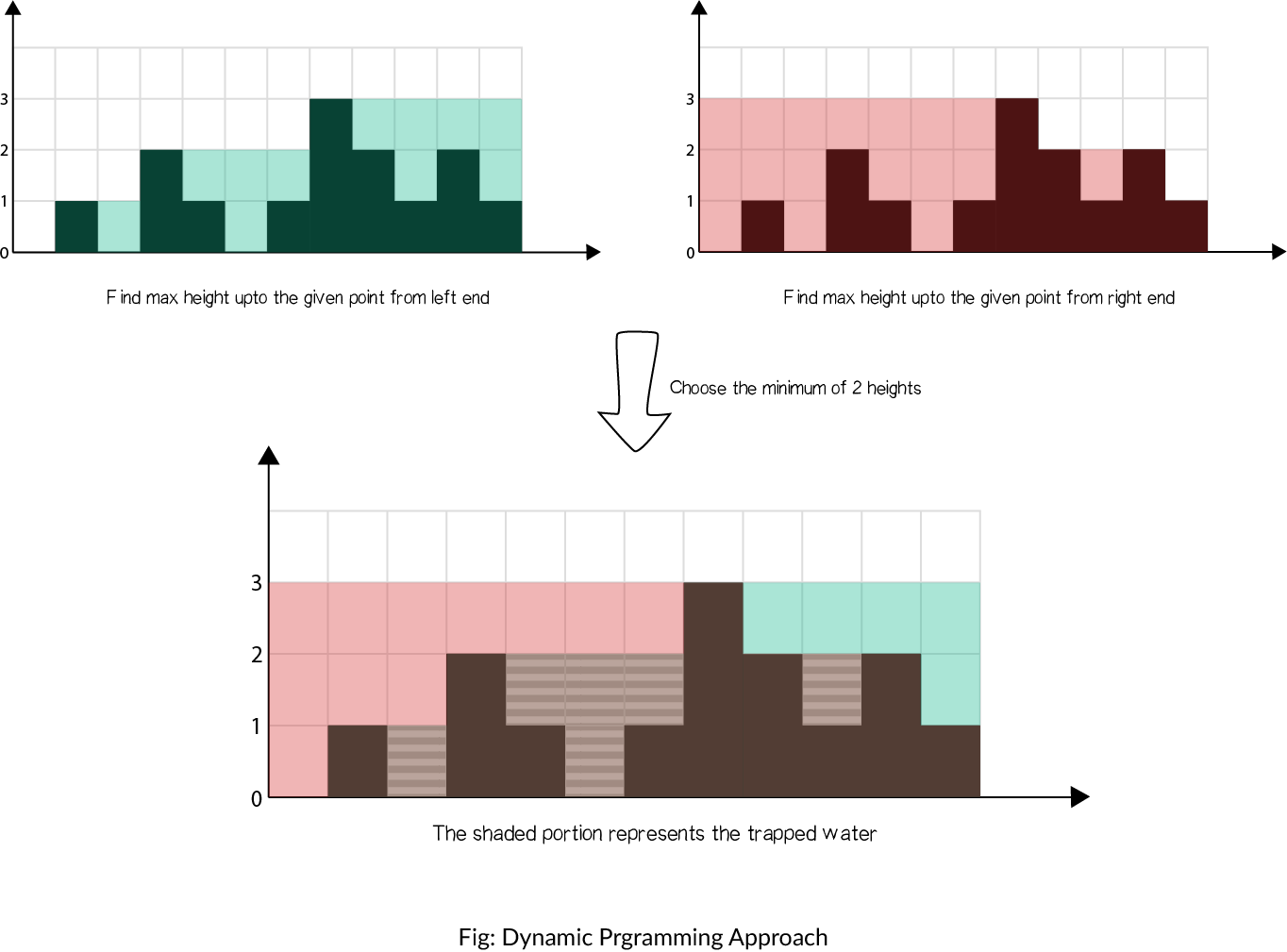
算法

• 找到数组中从下标 i 到最左端最高的条形块高度 $ext{left\_max}$。
• 找到数组中从下标 i 到最右端最高的条形块高度 $ext{right\_max}$。
• 扫描数组 $ext{height}$ 并更新答案：
  • 累加 $min( ext{max\_left}[i], ext{max\_right}[i]) - ext{height}[i]$ 到 $ans$ 上

• C++

int trap(vector<int>& height)
{
	if(height == null)
		return 0;
    int ans = 0;
    int size = height.size();
    vector<int> left_max(size), right_max(size);
    left_max[0] = height[0];
    for (int i = 1; i < size; i++) {
        left_max[i] = max(height[i], left_max[i - 1]);
    }
    right_max[size - 1] = height[size - 1];
    for (int i = size - 2; i >= 0; i--) {
        right_max[i] = max(height[i], right_max[i + 1]);
    }
    for (int i = 1; i < size - 1; i++) {
        ans += min(left_max[i], right_max[i]) - height[i];
    }
    return ans;
}

复杂性分析

• 时间复杂度：$O(n)$。

  • 存储最大高度数组，需要两次遍历，每次 $O(n)$ 。
  • 最终使用存储的数据更新$ext{ans}$ ，$O(n)$。

• 空间复杂度：$O(n)$ 额外空间。

  • 和方法 1 相比使用了额外的 $O(n)$ 空间用来放置 $ext{left\_max}$ 和 $ext{right\_max}$ 数组。
    
    
    
    

---

方法 3：栈的应用

直观想法

我们可以不用像方法 2 那样存储最大高度，而是用栈来跟踪可能储水的最长的条形块。使用栈就可以在一次遍历内完成计算。

我们在遍历数组时维护一个栈。如果当前的条形块小于或等于栈顶的条形块，我们将条形块的索引入栈，意思是当前的条形块被栈中的前一个条形块界定。如果我们发现一个条形块长于栈顶，我们可以确定栈顶的条形块被当前条形块和栈的前一个条形块界定，因此我们可以弹出栈顶元素并且累加答案到 $ext{ans}$ 。

算法

• 使用栈来存储条形块的索引下标。
• 遍历数组：
  • 当栈非空且 $ext{height}[current]> ext{height}[st.top()]$
    • 意味着栈中元素可以被弹出。弹出栈顶元素 $ext{top}$。
    • 计算当前元素和栈顶元素的距离，准备进行填充操作
      $ext{distance} = ext{current} - ext{st.top}() - 1$
    • 找出界定高度
      $ext{bounded\_height} = min( ext{height[current]}, ext{height[st.top()]}) - ext{height[top]}$
    • 往答案中累加积水量$ext{ans} mathrel{+}= ext{distance} imes ext{bounded\_height}$
  • 将当前索引下标入栈
  • 将 $ext{current}$ 移动到下个位置

• C++

int trap(vector<int>& height)
{
    int ans = 0, current = 0;
    stack<int> st;
    while (current < height.size()) {
        while (!st.empty() && height[current] > height[st.top()]) {
            int top = st.top();
            st.pop();
            if (st.empty())
                break;
            int distance = current - st.top() - 1;
            int bounded_height = min(height[current], height[st.top()]) - height[top];
            ans += distance * bounded_height;
        }
        st.push(current++);
    }
    return ans;
}

复杂性分析

• 时间复杂度：$O(n)$。
  • 单次遍历 $O(n)$ ，每个条形块最多访问两次（由于栈的弹入和弹出），并且弹入和弹出栈都是 $O(1)$ 的。
• 空间复杂度：$O(n)$。 栈最多在阶梯型或平坦型条形块结构中占用 $O(n)$ 的空间。
  
  
  
  

---

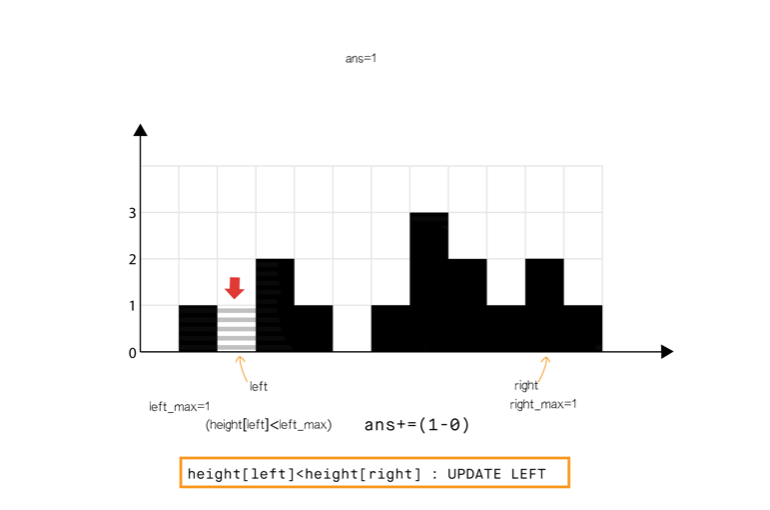
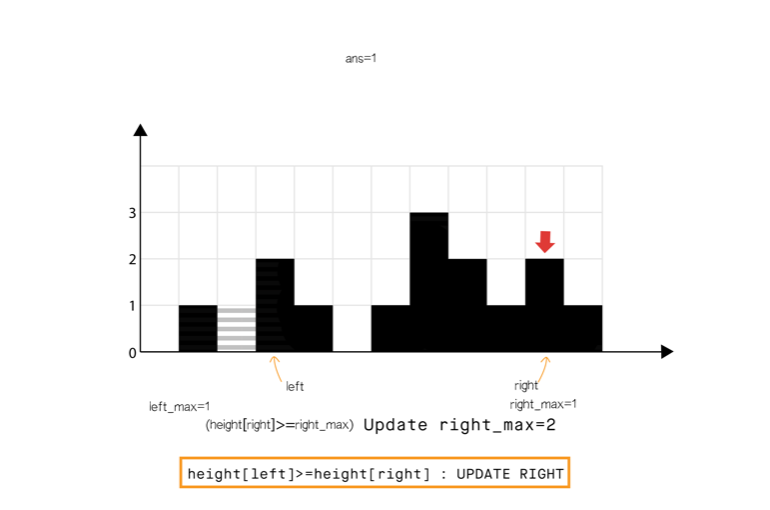
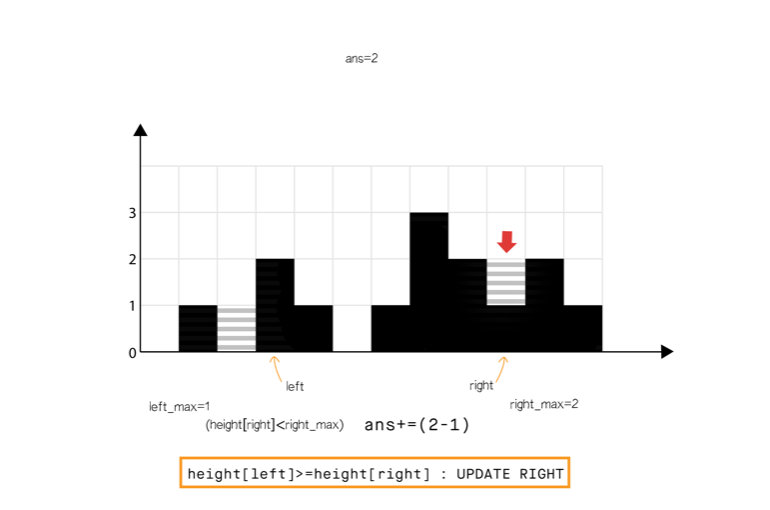
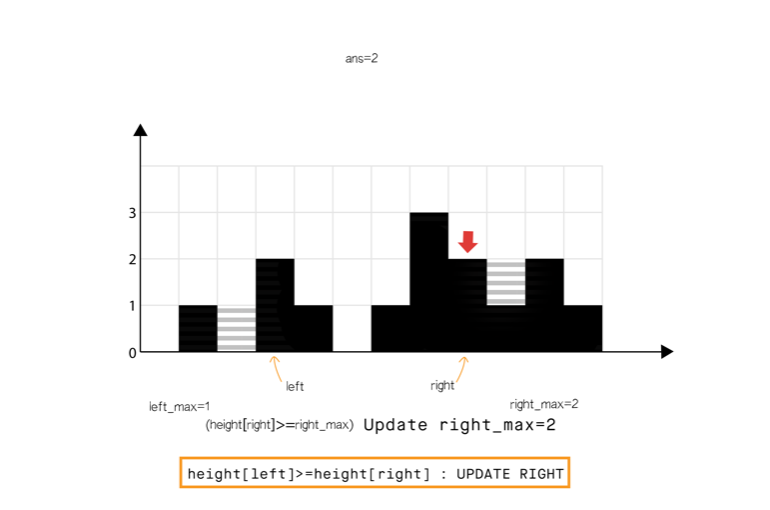
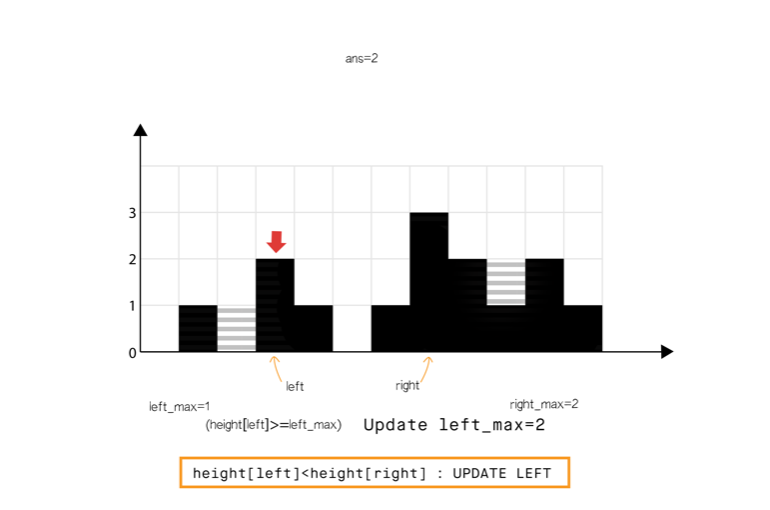
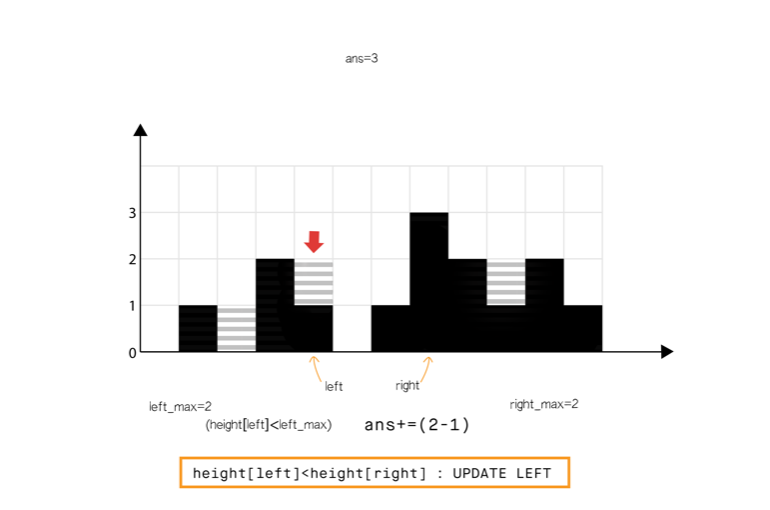
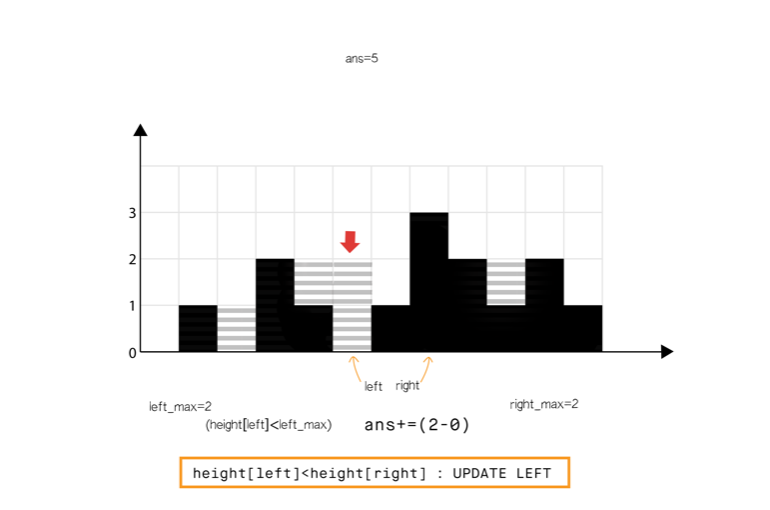
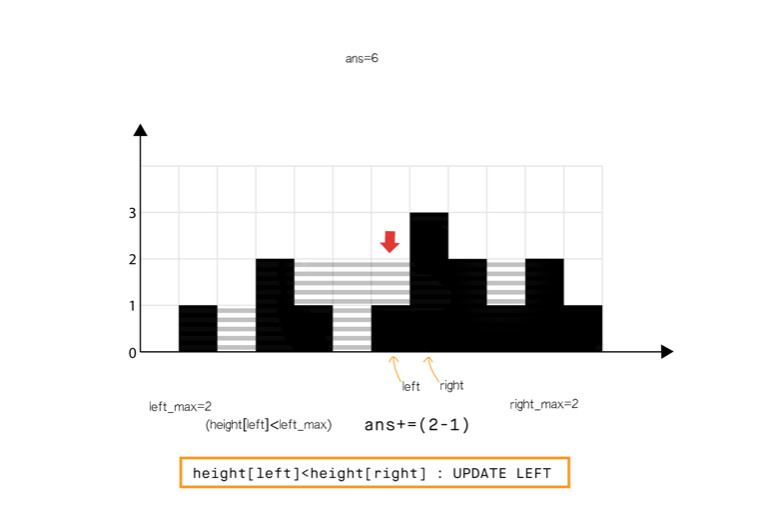
方法 4：使用双指针

直观想法

和方法 2 相比，我们不从左和从右分开计算，我们想办法一次完成遍历。
从动态编程方法的示意图中我们注意到，只要 $ext{right\_max}[i]> ext{left\_max}[i]$ （元素 0 到元素 6），积水高度将由 left_max 决定，类似地 $ext{left\_max}[i]> ext{right\_max}[i]$（元素 8 到元素 11）。
所以我们可以认为如果一端有更高的条形块（例如右端），积水的高度依赖于当前方向的高度（从左到右）。当我们发现另一侧（右侧）的条形块高度不是最高的，我们则开始从相反的方向遍历（从右到左）。
我们必须在遍历时维护 $ext{left\_max}$ 和 $ext{right\_max}$ ，但是我们现在可以使用两个指针交替进行，实现 1 次遍历即可完成。

算法

• 初始化 $ext{left}$ 指针为 0 并且 $ext{right}$ 指针为 size-1
• While $ext{left}< ext{right}$, do:
  • If $ext{height[left]}$ < $ext{height[right]}$
    • If $ext{height[left]} geq ext{left\_max}$, 更新 $ext{left\_max}$
    • Else 累加 $ext{left\_max}- ext{height[left]}$ 到 $ext{ans}$
    • $ext{left}$ = $ext{left}$ + 1.
  • Else
    • If $ext{height[right]} geq ext{right\_max}$, 更新 $ext{right\_max}$
    • Else 累加 $ext{right\_max}- ext{height[right]}$ 到 $ext{ans}$
    • $ext{right}$ = $ext{right}$ - 1.

1 / 11

• C++

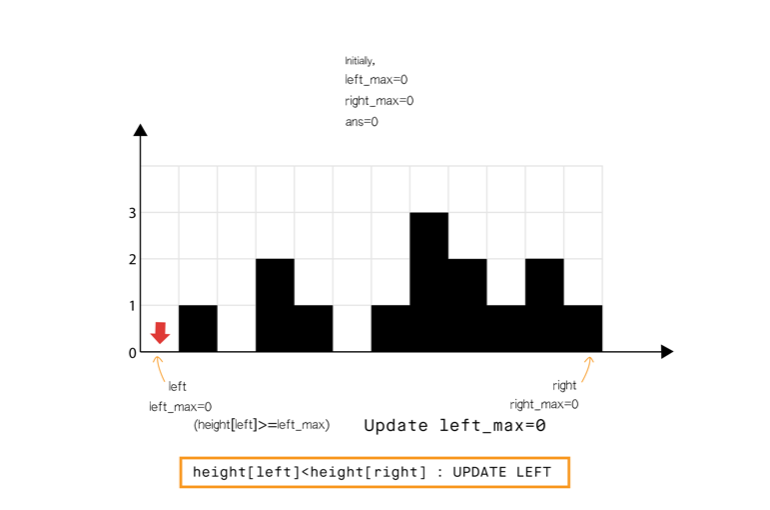
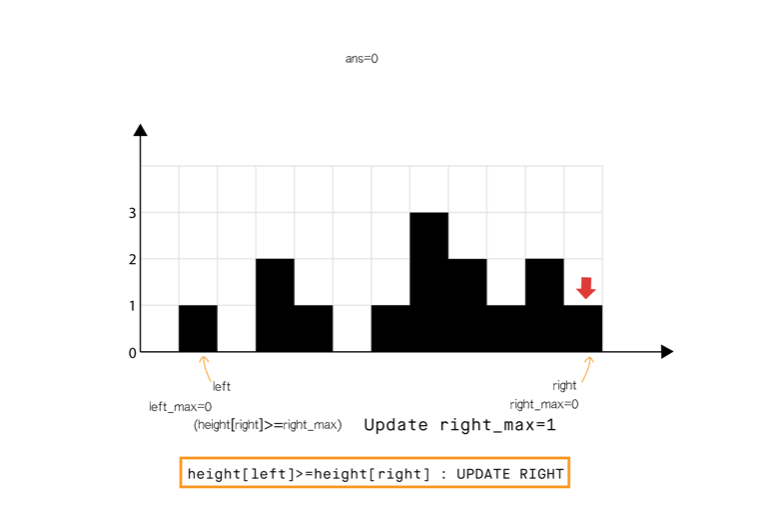
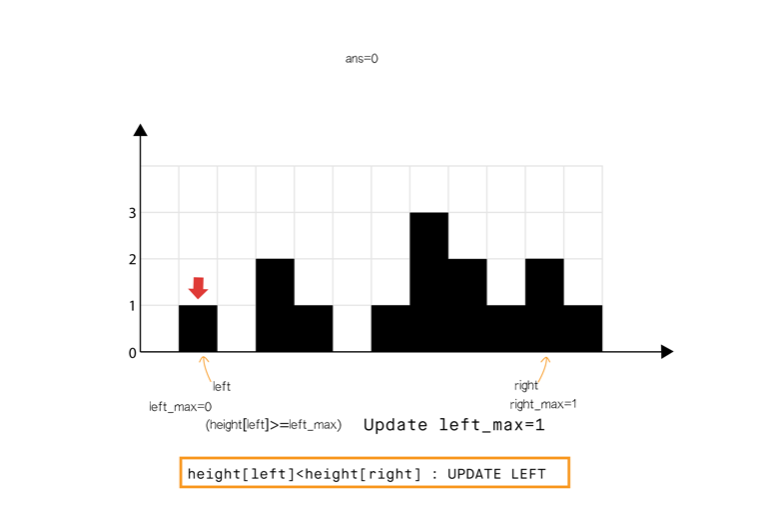
int trap(vector<int>& height)
{
    int left = 0, right = height.size() - 1;
    int ans = 0;
    int left_max = 0, right_max = 0;
    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
            ++left;
        }
        else {
            height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
            --right;
        }
    }
    return ans;
}

复杂性分析

• 时间复杂度：$O(n)$。单次遍历的时间$O(n)$。
• 空间复杂度：$O(1)$ 的额外空间。$ext{left}$, $ext{right}$, $ext{left\_max}$ 和 $ext{right\_max}$ 只需要常数的空间。