题目描述
我们从二叉树的根节点 root 开始进行深度优先搜索。
在遍历中的每个节点处,我们输出 D 条短划线(其中 D 是该节点的深度),然后输出该节点的值。(如果节点的深度为 D,则其直接子节点的深度为 D + 1。根节点的深度为 0)。
如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出 S,还原树并返回其根节点 root。
示例:
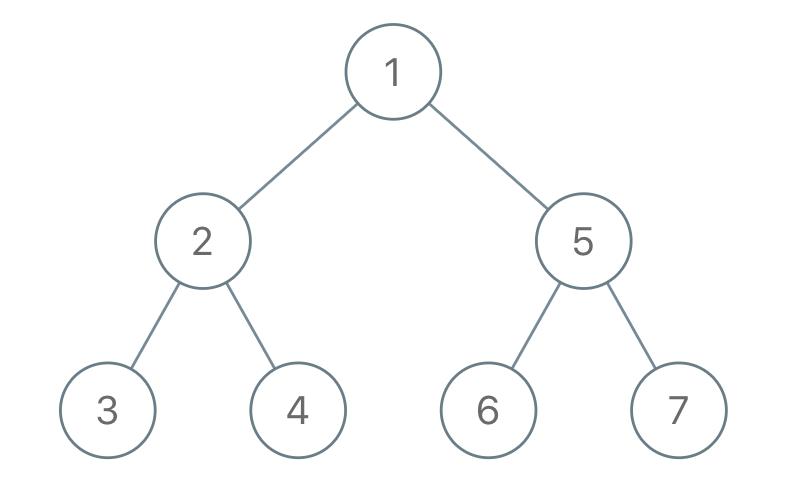
输入:"1-2--3--4-5--6--7"
输出:[1,2,5,3,4,6,7]
题目链接: https://leetcode-cn.com/problems/recover-a-tree-from-preorder-traversal/
思路
使用递归来做。代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* recoverFromPreorder(string S) {
if(S=="") return nullptr;
int curPos = 0; // 当前位置
int curLevel = 0; // 当前所在的层数
TreeNode* root = recover(S, curPos, curLevel);
return root;
}
TreeNode* recover(string s, int& curPos, int curLevel){
int nextLevel = 0; // 下一层的层数
while(curPos<s.length() && s[curPos]==\'-\'){ // 计算\'-\'的个数,也是下一层的层数
curPos++;
nextLevel++;
}
// 如果下一层的层数小于当前层,则返回
if(nextLevel<curLevel || curPos>=s.length()){ // 注意条件的后一部分
curPos -= nextLevel;
return nullptr;
}
int begin = curPos;
while(curPos<s.length() && isdigit(s[curPos])) curPos++;
int num = stoi(s.substr(begin, curPos-begin));
TreeNode* root = new TreeNode(num);
root->left = recover(s, curPos, curLevel+1);
root->right = recover(s, curPos, curLevel+1);
return root;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(h)