leetcode题解之最接近的三数之和
Posted 刷题之路1
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode题解之最接近的三数之和相关的知识,希望对你有一定的参考价值。
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1 输出:2 解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
提示:
3 <= nums.length <= 10^3-10^3 <= nums[i] <= 10^3-10^4 <= target <= 10^4
解题方案
思路
- 标签:排序和双指针
- 本题目因为要计算三个数,如果靠暴力枚举的话时间复杂度会到 ,需要降低时间复杂度
- 首先进行数组排序,时间复杂度
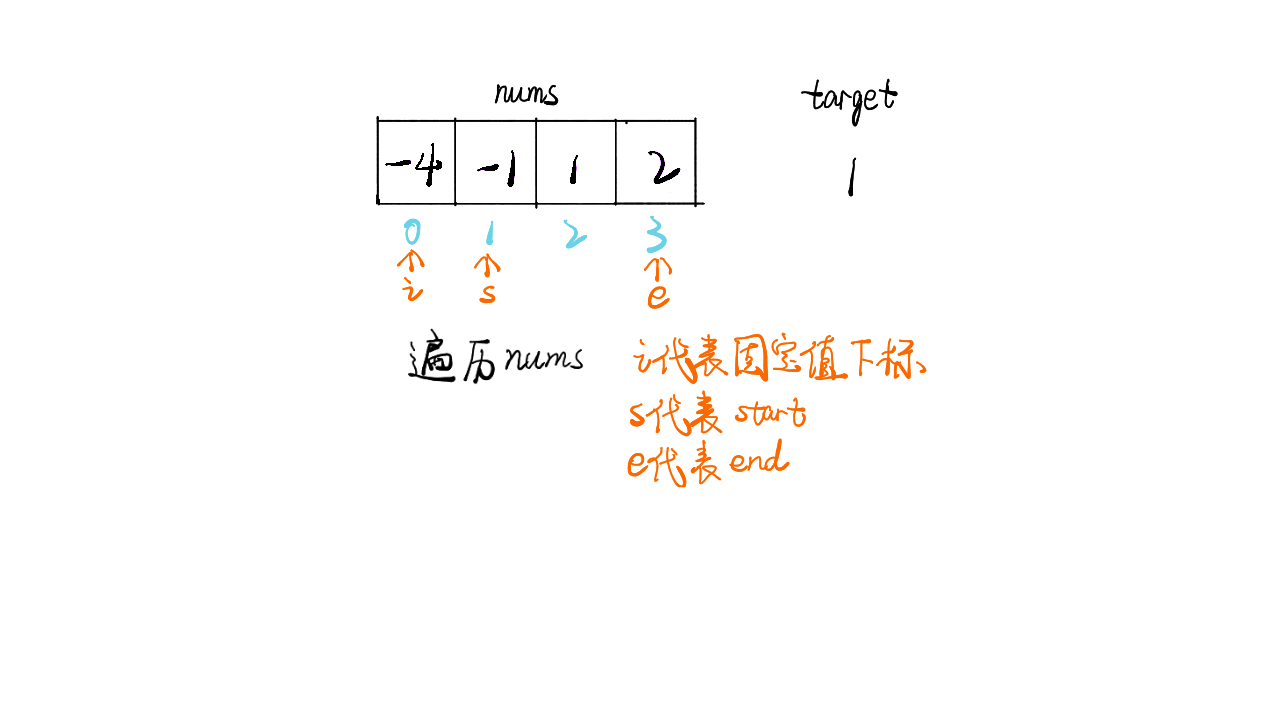
- 在数组 nums 中,进行遍历,每遍历一个值利用其下标i,形成一个固定值 nums[i]
- 再使用前指针指向
start = i + 1处,后指针指向end = nums.length - 1处,也就是结尾处 - 根据
sum = nums[i] + nums[start] + nums[end]的结果,判断 sum 与目标 target 的距离,如果更近则更新结果 ans - 同时判断 sum 与 target 的大小关系,因为数组有序,如果
sum > target则end--,如果sum < target则start++,如果sum == target则说明距离为 0 直接返回结果 - 整个遍历过程,固定值为 n 次,双指针为 n 次,时间复杂度为
- 总时间复杂度:
代码
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int ans = nums[0] + nums[1] + nums[2];
for(int i=0;i<nums.length;i++) {
int start = i+1, end = nums.length - 1;
while(start < end) {
int sum = nums[start] + nums[end] + nums[i];
if(Math.abs(target - sum) < Math.abs(target - ans))
ans = sum;
if(sum > target)
end--;
else if(sum < target)
start++;
else
return ans;
}
}
return ans;
}
}
画解
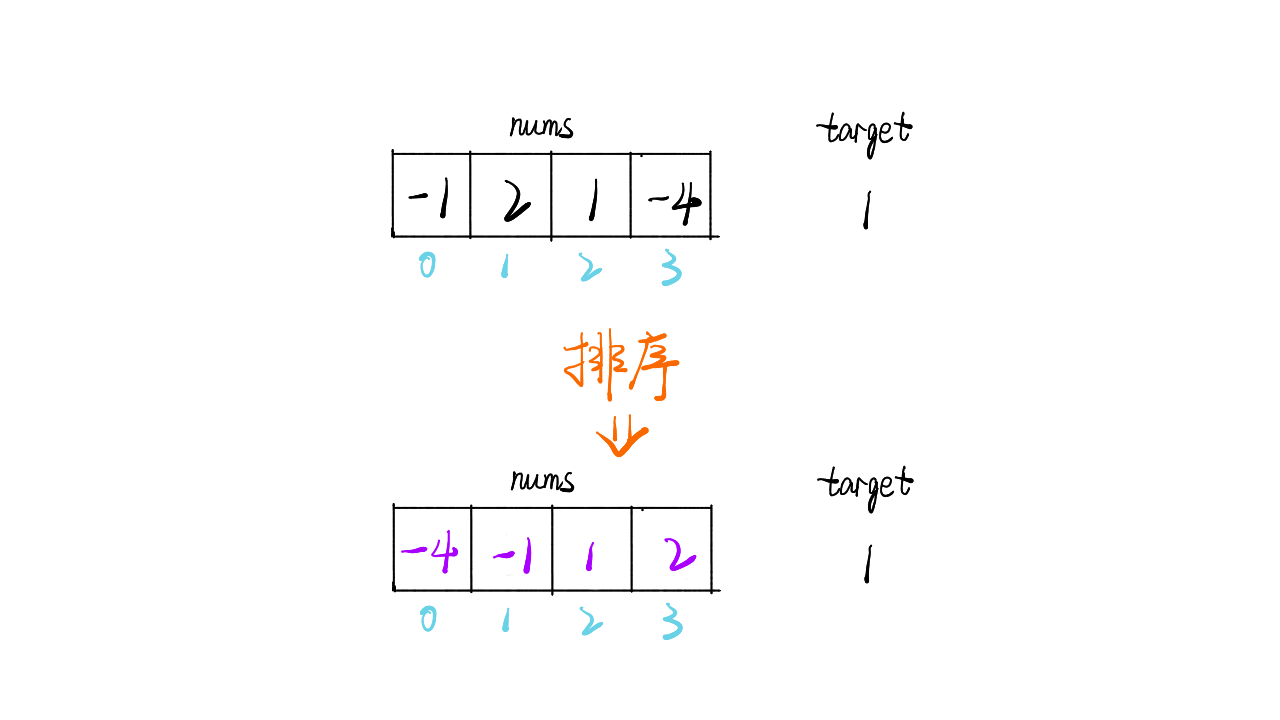
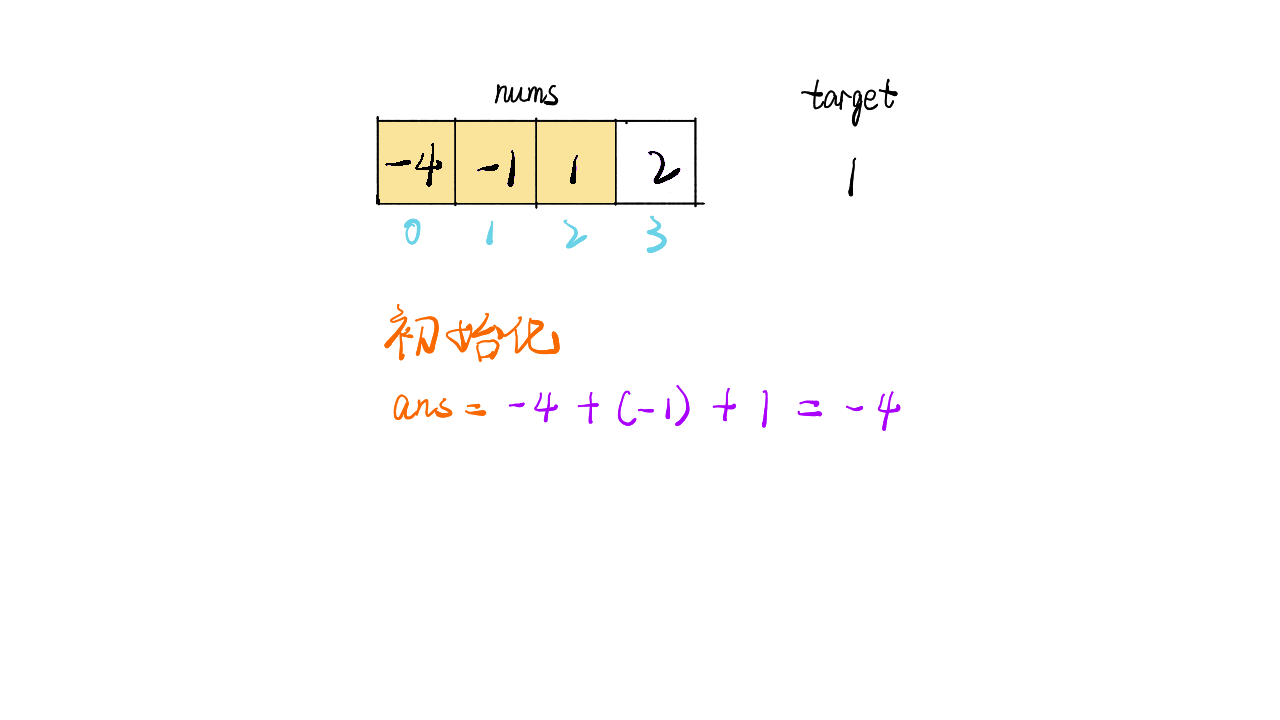
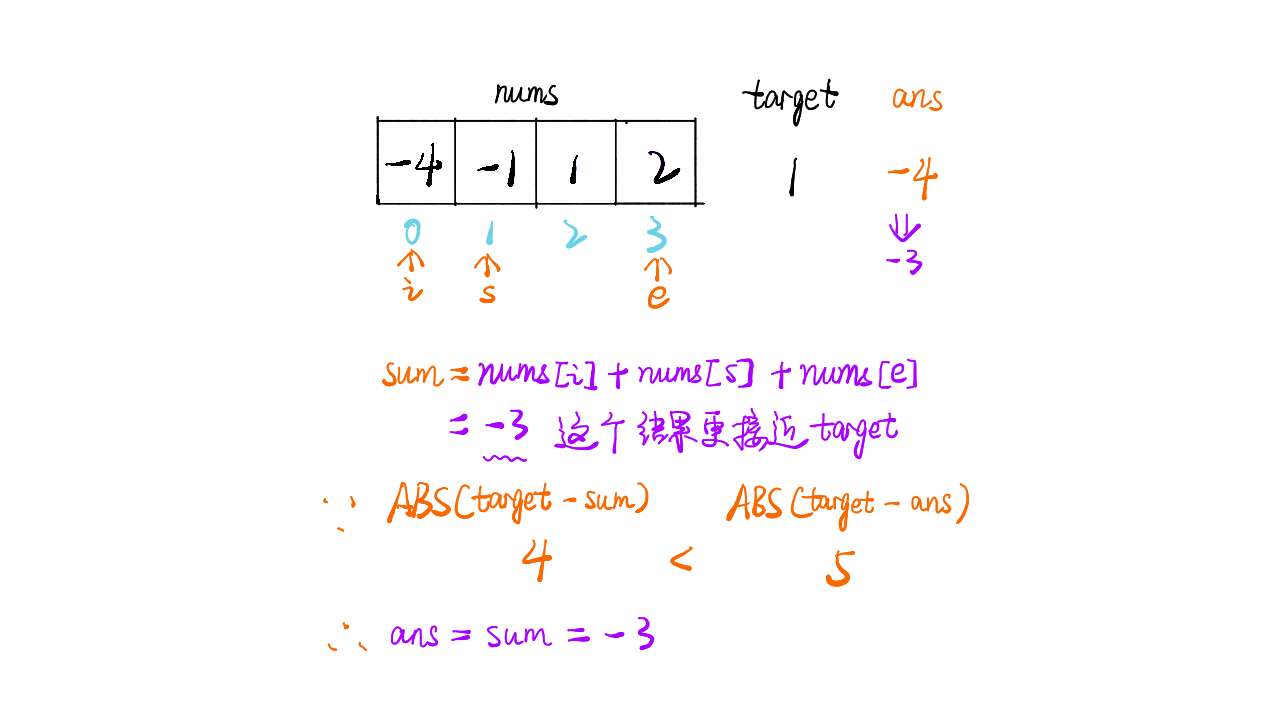
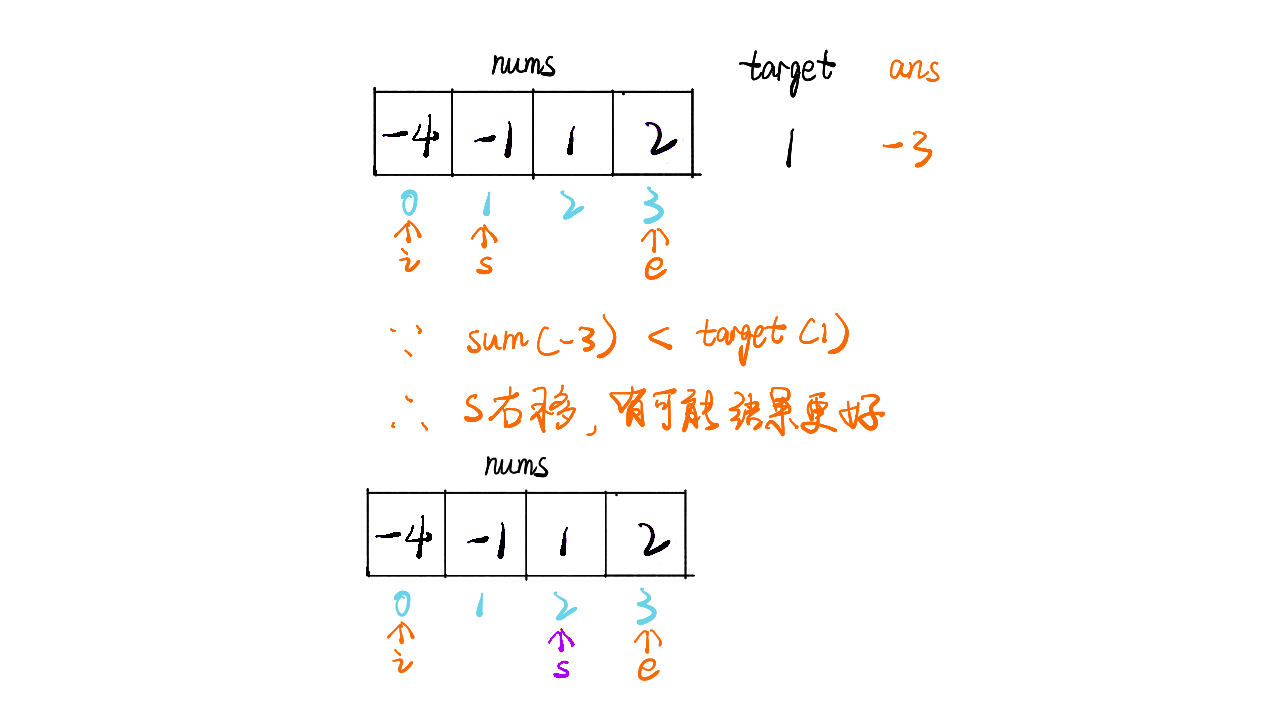
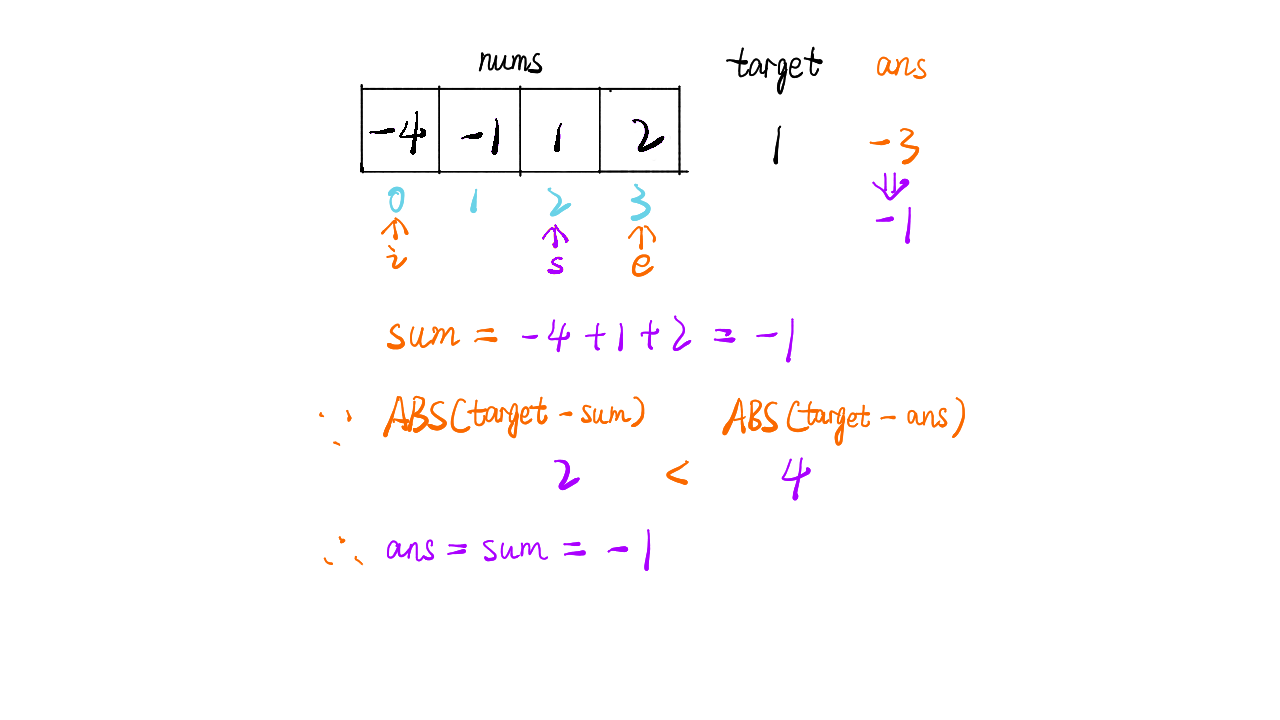
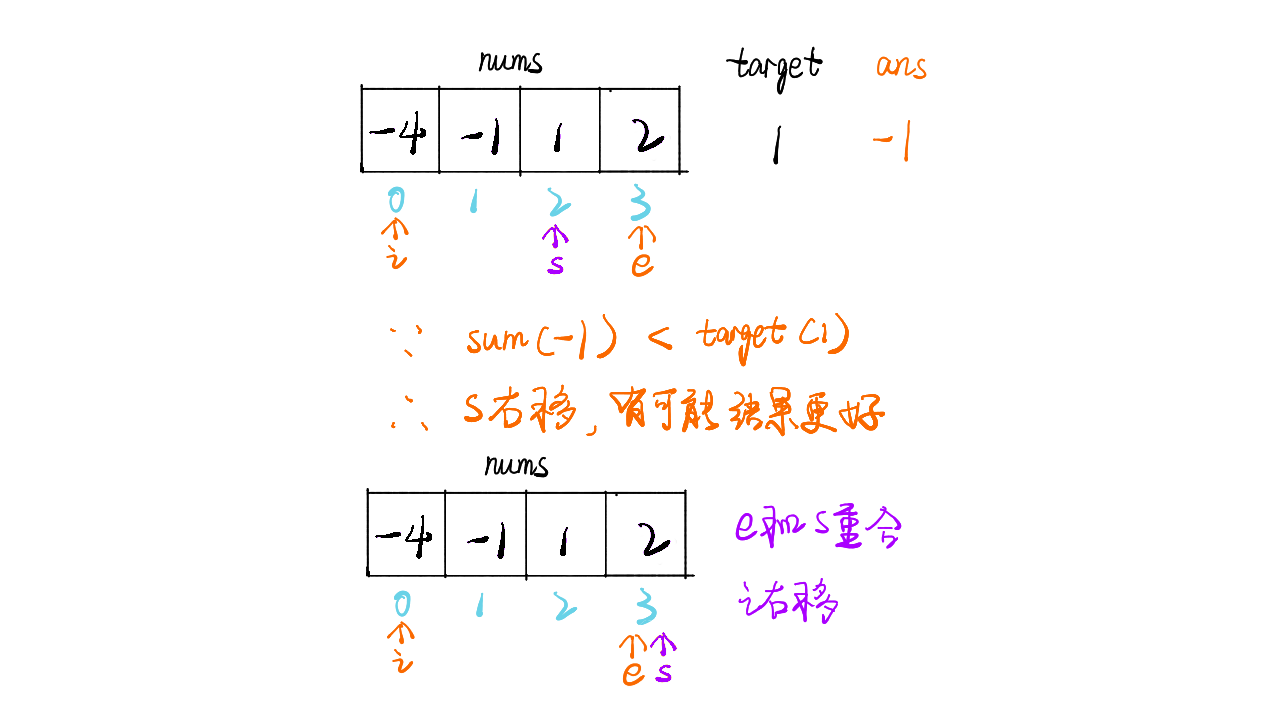
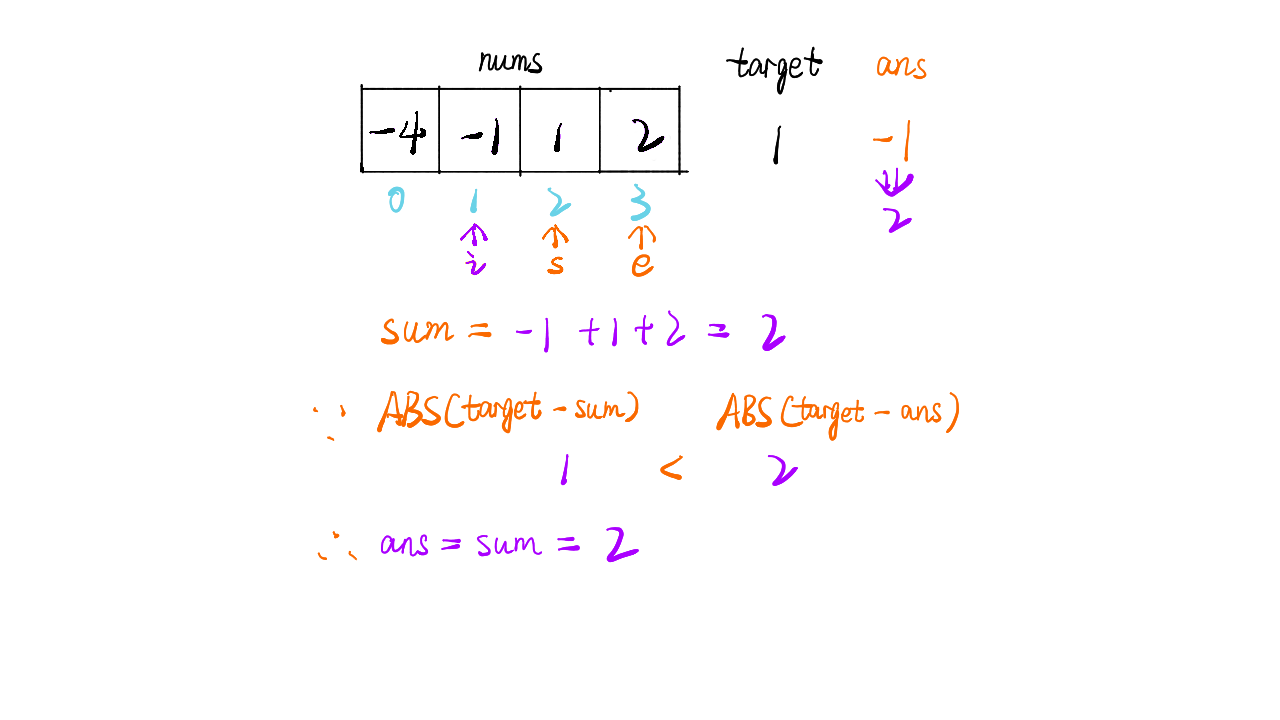
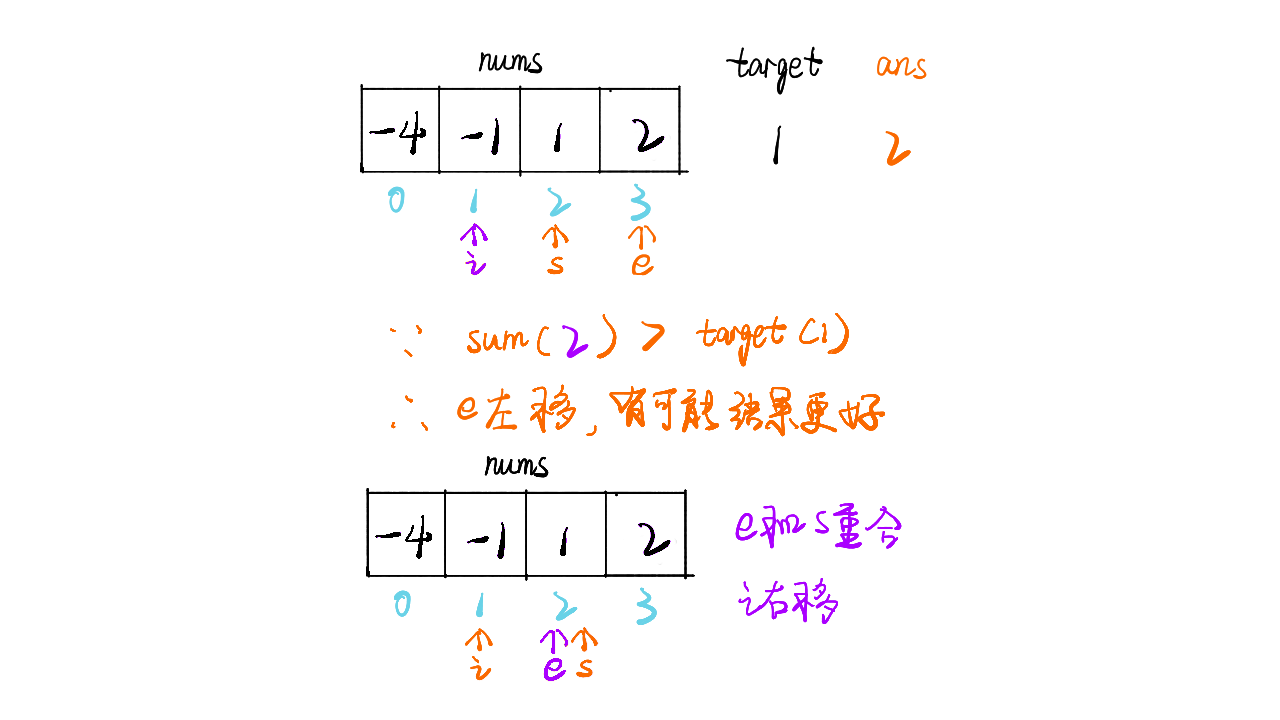
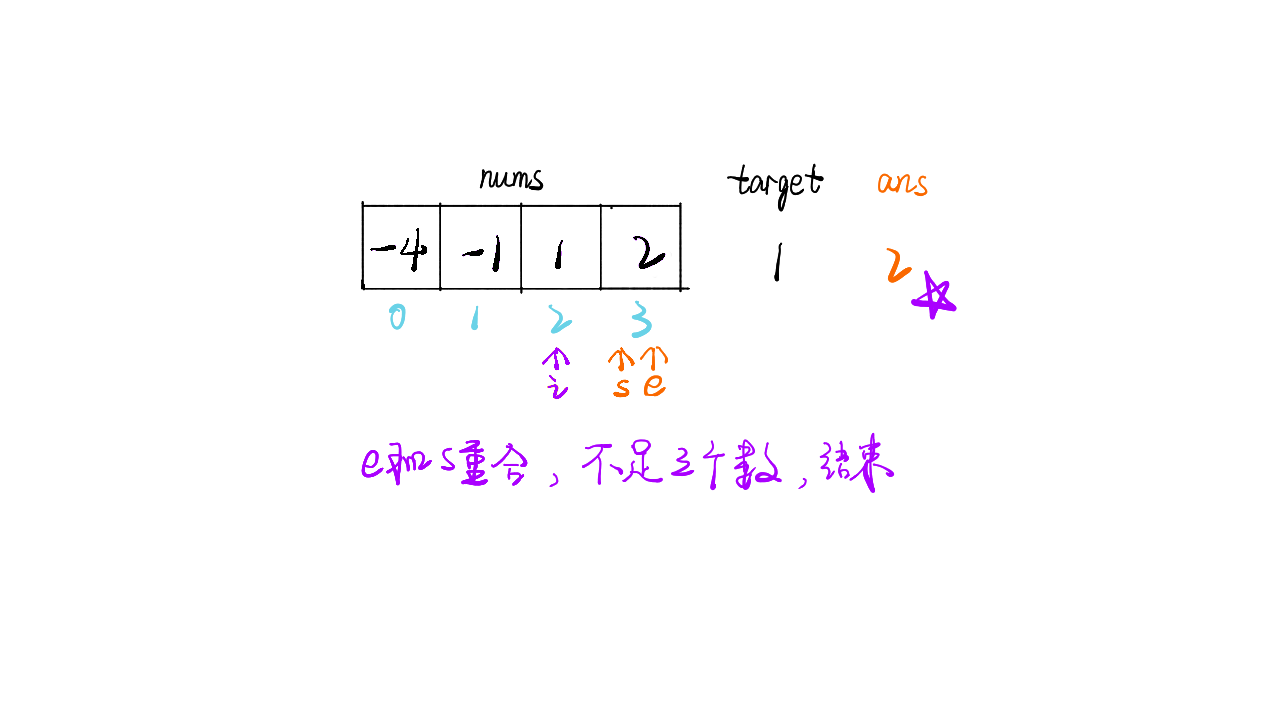

1 / 11
点击我的头像加关注,和我一起打卡天天算法
以上是关于leetcode题解之最接近的三数之和的主要内容,如果未能解决你的问题,请参考以下文章
算法leetcode|16. 最接近的三数之和(rust重拳出击)