Q:在一个 2 x 3 的板上(board)有 5 块砖瓦,用数字 1~5 来表示, 以及一块空缺用 0 来表示.一次移动定义为选择 0 与一个相邻的数字(上下左右)进行交换.最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。
给出一个谜板的初始状态,返回最少可以通过多少次移动解开谜板,如果不能解开谜板,则返回 -1 。
示例:
输入:board = [[1,2,3],[4,0,5]]
输出:1
解释:交换 0 和 5 ,1 步完成
输入:board = [[1,2,3],[5,4,0]]
输出:-1
解释:没有办法完成谜板
输入:board = [[4,1,2],[5,0,3]]
输出:5
解释:
最少完成谜板的最少移动次数是 5 ,
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]
输入:board = [[3,2,4],[1,5,0]]
输出:14
提示:
board 是一个如上所述的 2 x 3 的数组.
board[i][j] 是一个 [0, 1, 2, 3, 4, 5] 的排列.
A:
1.BFS算法(引用自:labuladong)
对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法。
这个题目转化成 BFS 问题是有一些技巧的,我们面临如下问题:
1、一般的 BFS 算法,是从一个起点start开始,向终点target进行寻路,但是拼图问题不是在寻路,而是在不断交换数字,这应该怎么转化成 BFS 算法问题呢?
2、即便这个问题能够转化成 BFS 问题,如何处理起点start和终点target?
首先回答第一个问题,BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。明白了这个道理,我们的问题就转化成了:如何穷举出board当前局面下可能衍生出的所有局面?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
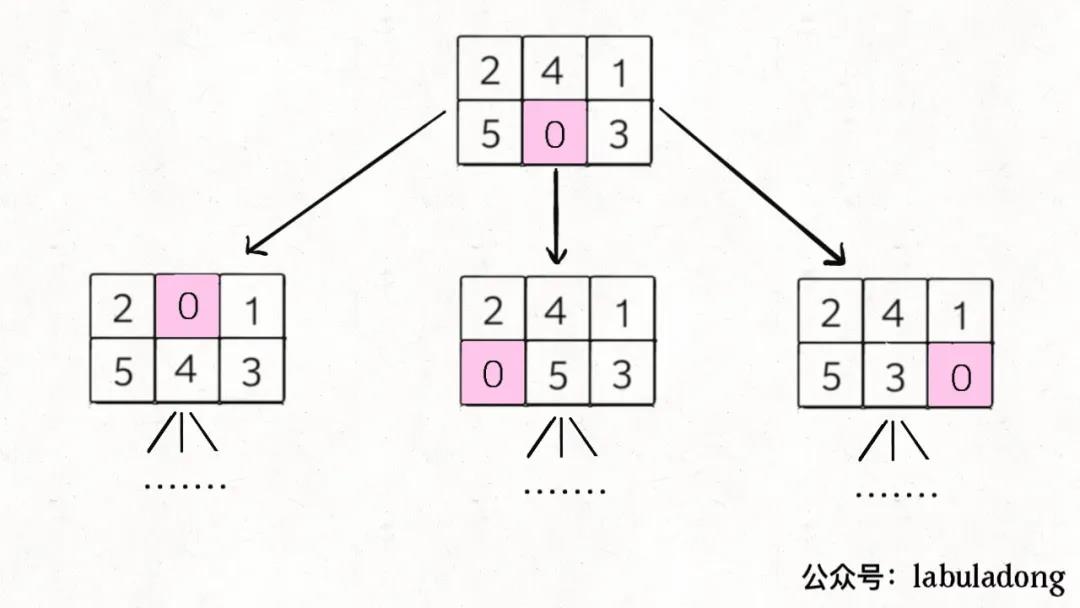
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达target时,就得到了赢得游戏的最少步数。
对于第二个问题,我们这里的board仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?很简单,我们只要手动写出来这个映射就行了:
List<List<Integer>> neighbor = new ArrayList<>();
neighbor.add(Arrays.asList(1, 3));
neighbor.add(Arrays.asList(0, 4, 2));
neighbor.add(Arrays.asList(1, 5));
neighbor.add(Arrays.asList(0, 4));
neighbor.add(Arrays.asList(3, 1, 5));
neighbor.add(Arrays.asList(4, 2));
这个含义就是,在一维字符串中,索引i在二维数组中的的相邻索引为neighbor[i]:
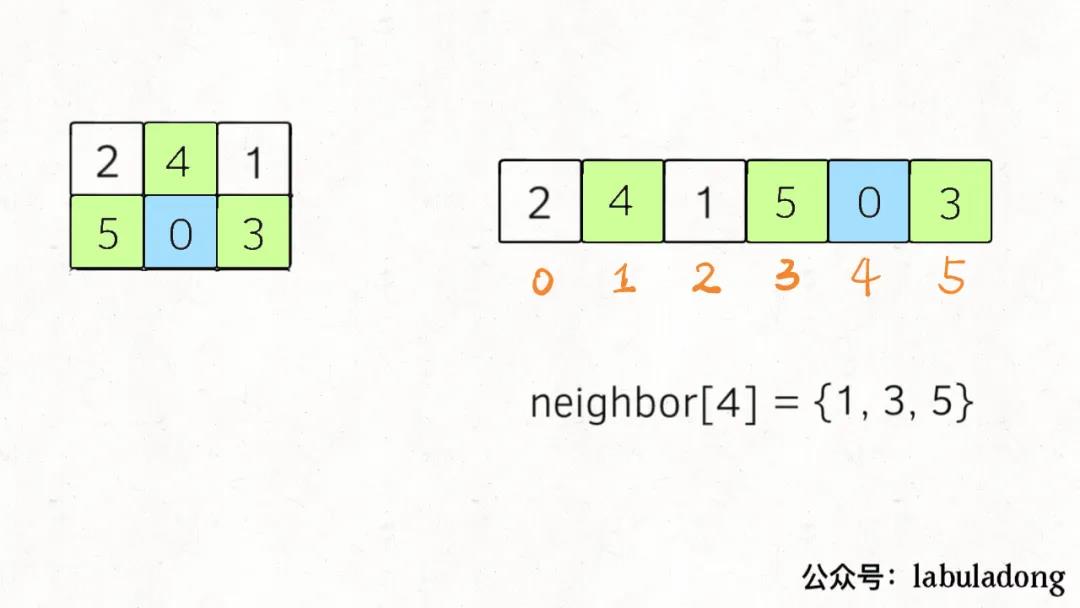
至此,我们就把这个问题完全转化成标准的 BFS 问题了。
public int slidingPuzzle(int[][] board) {
int m = 2, n = 3;
String start = "";
String target = "123450";
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
start += board[i][j];
}
}
//每个位置的邻居位置
List<List<Integer>> neighbor = new ArrayList<>();
neighbor.add(Arrays.asList(1, 3));
neighbor.add(Arrays.asList(0, 4, 2));
neighbor.add(Arrays.asList(1, 5));
neighbor.add(Arrays.asList(0, 4));
neighbor.add(Arrays.asList(3, 1, 5));
neighbor.add(Arrays.asList(4, 2));
Queue<String> q = new LinkedList<>();
//防止走回头路,这里最好用String而不是StringBuilder,否则判断contains时会对比不出来
Set<String> visited = new HashSet<>();
q.add(start);
visited.add(start);
int step = 0;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
String curr = q.poll();
if (curr.equals(target)) {
return step;
}
//找0的位置
int idx = 0;
for (; curr.charAt(idx) != \'0\'; idx++) ;
//对0位置的每个邻居交换
for (int adj : neighbor.get(idx)) {
//swap adj和idx 位置
char[] new_board = curr.toCharArray();
char temp = new_board[adj];
new_board[adj] = new_board[idx];
new_board[idx] = temp;
String new_n_board = new String(new_board);
//没走过的路加入
if (!visited.contains(new_n_board)) {
q.add(new_n_board);
visited.add(new_n_board);
}
}
}
step++;
}
return -1;
}
2.A*搜索算法
思路:基于普通的广度优先遍历解法, 将普通队列改为使用优先队列, 每次队列poll时都先通过compareTo选择一个"曼哈顿距离最短", 也就是距离最终结果需要交换次数最小的一个分支进行计算。像这样每次队列都择优poll, BFS算法就能够更快速的到达终点。
关于曼哈顿距离:二维坐标中, 一个点(x1, y1)到另一个点(x2, y2)的曼哈顿距离 = |x1 - x2| + |y1 - y2|
由于优先队列默认队列头元素是最小元素,故我们可以拿来作为小根堆使用, 故这个A* 算法的主要思想就是每次都poll一个交换次数 + 曼哈顿距离最短的节点, 从而达到枝减的效果
public int slidingPuzzle(int[][] board) {
int[][] dir = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};
int[] endBoard = {1, 2, 3, 4, 5, 0};
ANode curr = new ANode(board);
if (Arrays.equals(curr.board, endBoard))
return 0;
PriorityQueue<ANode> queue = new PriorityQueue<>();
queue.offer(curr);
HashSet<ANode> visited = new HashSet<>();
visited.add(curr);
while (!queue.isEmpty()) {
curr = queue.poll();
for (int nextZeroPos : dir[curr.zeroPos]) {
int[] nextBoard = Arrays.copyOf(curr.board, 6);
swap(nextBoard, curr.zeroPos, nextZeroPos);
if (Arrays.equals(nextBoard, endBoard))
return curr.count + 1;
ANode next = new ANode(nextBoard, nextZeroPos, curr.count + 1);
if (visited.contains(next))
continue;
queue.offer(next);
visited.add(next);
}
}
return -1;
}