平衡二叉树(AVL树)深入解读
Posted zxnsirius
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了平衡二叉树(AVL树)深入解读相关的知识,希望对你有一定的参考价值。
平衡二叉树又称AVL树
性质:
它或者是颗空树,或者是具有下列性质的二叉树:
- 它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
- 若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有节点的平衡因子只可能为-1,0,1.
- 只要二叉树上有一个节点的平衡因子的绝对值大于1,那么这颗平衡二叉树就失去了平衡。
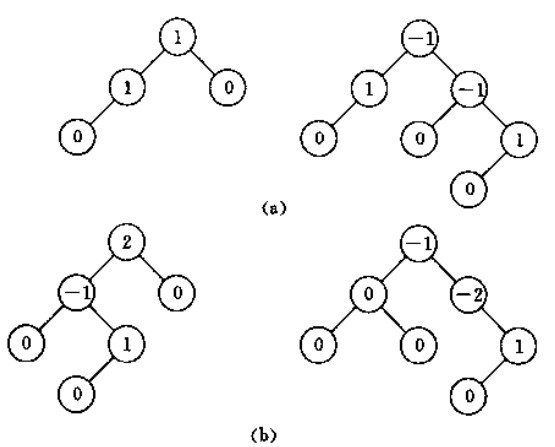
根据上述性质我们可以发现图(a)是一棵平衡二叉树,而图(b)是一棵不平衡二叉树。图中结点的数值代表的就是当前结点的平衡因子。也验证了上述性质,一棵平衡二叉树的所有结点的平衡因子只可能是-1、0、1三种。
为什么需要平衡二叉树?
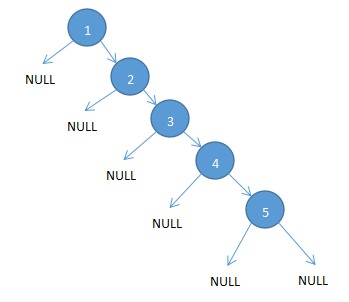
当然,我们都希望所有的二叉排序树的初始序列都是平衡的,因为平衡二叉树上的任何一个结点左右字数的深度之差都不会超过1,则可以证明它的深度和logn是同数量级的,所以其平均查找长度也和logn同数量级。但是事于愿违有些二叉排序树的插入,或者初始序列由于其插入的先后顺序等缘故,将导致我们的二叉排序树的效率大大降低。如下图
以上是关于平衡二叉树(AVL树)深入解读的主要内容,如果未能解决你的问题,请参考以下文章