线代--矩阵的分解-LU分解n阶方阵

Posted 2023-05-13

参考技术A

矩阵分解的概念： 初中我们接触过数的分解,如: ;推广到矩阵，一个矩阵也可以分解为几个矩阵乘积的形式，矩阵分解具有不同的目的。

矩阵的LU分解的定义 是将矩阵 分解为一个下三角矩阵( )和上三角矩阵( )乘积的方式: ，其目的是为了提高计算效率。

一个矩阵可以进行LU分解的前提条件 ：对矩阵 的消元过程中不能涉及行交换操作(只有主元位置为0的矩阵在高斯消元过程需要进行行变换)。因为分解得到的 矩阵是由单位矩阵得到的，如果消元过程发生了行交换，也就意味着单位矩阵发生了行交换，对应的L矩阵就不是一个下三角矩阵。
证明如下：

当一个矩阵不用发生行交换进行消元过程的时候，那么对应获取它的 矩阵直接可以通过 矩阵取反得到，发生行交换后， 矩阵不能直接由 矩阵取反得到。

分解的时间复杂度的计算
其中 是矩阵 下三角区域需要化为 的元素的个数(一共约为 个)，完成这些元素的消元约需要进行 次初等变换，而每次初等变换意味着对矩阵内一行的 个元素都进行了一次运算，所以由 高斯消元过程总共约发生了 次数据运算, 时间复杂度约为 。由于高斯消元过程在得到 矩阵的同时，每次初等变换操作的值取反往单位矩阵 相应的位置进行填充就可以得到 矩阵，所以整体上 分解过程的时间消耗近乎等于 过程的时间。

对于解线性系统


设 , 方程变为 ,求出 的时间复杂度约为 。
同样，对于 ,求出 的时间复杂度也约为
从而，将矩阵 通过 分解，时间复杂度总体为

分解计算时间复杂度相比求解矩阵的逆的过程求解 .
矩阵通过增广矩阵的形式求逆的时间复杂度为 ，增广矩阵有 个元素要执行消元操作。然后再求解 的时间复杂度有 次操作，所以通过矩阵的逆的方法求解线性系统的时间复杂度为 。

综上，LU分解求解线性系统的效率是比较高的。

矩阵分解---QR正交分解，LU分解

相关概念：

• 正交矩阵：若一个方阵其行与列皆为正交的单位向量，则该矩阵为正交矩阵，且该矩阵的转置和其逆相等。两个向量正交的意思是两个向量的内积为 0
• 正定矩阵：如果对于所有的非零实系数向量x ，都有 x‘Ax>0，则称矩阵A 是正定的。正定矩阵的行列式必然大于 0， 所有特征值也必然 > 0。相对应的，半正定矩阵的行列式必然 ≥ 0。

 

QR分解

矩阵的正交分解又称为QR分解，是将矩阵分解为一个正交矩阵Q和一个上三角矩阵的乘积的形式。

任意实数方阵A，都能被分解为A=QR。这里的Q为正交单位阵，即QTQ=I。R是一个上三角矩阵。这种分解被称为QR分解。

QR分解也有若干种算法，常见的包括Gram–Schmidt、Householder和Givens算法。

QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。用一张图可以形象地表示QR分解： 

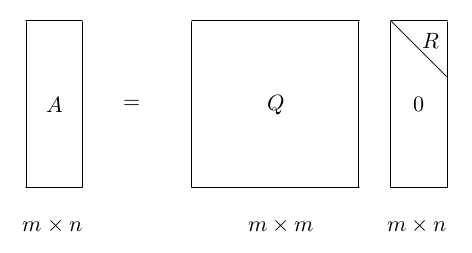
这其中， Q为正交矩阵，R为上三角矩阵。 
实际中，QR分解经常被用来解线性最小二乘问题。

 

• 计算方法：

 

• 对于非方阵的m∗n(m≥n)阶矩阵A也可能存在QR分解。这时Q为m*m阶的正交矩阵，R为m*n阶上三角矩阵。这时的QR分解不是完整的(方阵)，因此称为约化QR分解(对于列满秩矩阵A必存在约化QR分解)。同时也可以通过扩充矩阵A为方阵或者对矩阵R补零，可以得到完全QR分解。

LU分解---三角分解

    矩阵的LU分解是将一个矩阵分解为一个下三角矩阵与上三角矩阵的乘积。本质上，LU分解是高斯消元的一种表达方式。首先，对矩阵A通过初等行变换将其变为一个上三角矩阵。对于学习过线性代数的同学来说，这个过程应该很熟悉，线性代数考试中求行列式求逆一般都是通过这种方式来求解。然后，将原始矩阵A变为上三角矩阵的过程，对应的变换矩阵为一个下三角矩阵。这中间的过程，就是Doolittle algorithm(杜尔里特算法)。

    

计算方法：

 

    LU分解常用来求解线性方程组，求逆矩阵或者计算行列式。例如在计算行列式的时候，，。而对于三角矩阵来说，行列式的值即为对角线上元素的乘积。所以如果对矩阵进行三角分解以后再求行列式，就会变得非常容易。

    在线性代数中已经证明，如果方阵是非奇异的，即的行列式不为0，LU分解总是存在的。

 

 

 

 

参考： https://blog.csdn.net/qq_30981697/article/details/71545519

        https://blog.csdn.net/eric_e/article/details/80354834

来自为知笔记(Wiz)