计算机二进制，十进制，八进制，十六进制怎么转换

Posted 2023-05-13

谁可以告诉我，计算机，十进制，八进制，十进制，十六进制到底怎么转换啊！老师讲的太烦了，我搞不清楚怎么转换，哪位有什么技巧吗？好着急啊！

十进制转换：

1234[10进制] 0 1 2 3 4 5 6 7 8 9 0 当数位上的值超过9就要进1

1000+200+30+4=1*103+2*102+3*101+4*100=1234。

21011[2进制] 0 1 当数位上的值超过1就要进1

1*23+0*22+1*21+1*20=8+0+2+1=11。

1011[8进制]0 1 2 3 4 5 6 7 当数位上的值超过7就要进1

1*83+1*81+1*80=512+8+1=521。

1011[16进制]0 1 2 3 4 5 6 7 8 9 A B C D E F 当数位上的值超过15就要进1

1*163+1*161+1*160=4096+16+1=4113。

二进制转换：

1、十进制到二进制:除2取余数 最后把余数倒过来 100101

比如：十进制数37

所以转换成的二进制数字为:100101

2、八进制到二进制：一个八进制的位拆分成一个三位的二进制数

比如：[八进制]616

6拆分成 110

1拆分成 001

6拆分成 110

所以转换成的二进制数字为:110001110

3、十六进制到二进制：一个八进制的位拆分成一个四位的二进制数

比如：[十六进制]616

6拆分成 0110

1拆分成 0001

6拆分成 0110

所以转换成的二进制数字为:11000010110

八进制转换：

1、十进制到八进制：除8取余数 最后把余数倒过来

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成八进制 

比如:2456 转化成八进制数字：4630

2456/8=307，余0；
307/8=38，余3；
38/8=4，余6；
4/8=0，余4。
将所有余数倒序相连，得到结果：4630。
因此十进制的2456转换为八进制结果为4630。

2、二进制到八进制转换  7=4+2+1 111 八进制最大的数字是7转换成二进制刚好是111，占3个位

每三个二进制数为一组，转成一个八进制数位，如果二进制高位不足3位时，用零填补。

比如：10011011

010 011 011

2     3     3

因此二进制的10011011转换为八进制结果为233。

十六进制转换：

1、十进制到十六进制：除16倒着取余数

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成十六进制 

比如说：1610转换成十六进制

直接转16进制：
1610/16=100……10(A)；
100 /16= 6……4；
6 /16= 0……6；

故：1610(10)=64A(16).

2、二进制到十六进制 15=8+4+2+1   1111 十六进制最大数字是F,即15转换成二进制1111，刚好占4个位

每四个二进制数为一组，转成一个十六进制数位，如果二进制高位不足3位时，用零填补。

比如：1110011011

0011 1001 1011

3       9      B

因此二进制的 1110011011转换为十六进制39B

拓展资料：

2进制，是供计算机使用的，1，0代表开和关，有和无，机器只认识2进制。

10进制，当然是便于我们人类来使用，我们从小的习惯就是使用十进制，这个毋庸置疑。

16进制，内存地址空间是用16进制的数据表示, 如0x8049324。

编程中，我们常用的还是10进制。 　　

比如：int a = 100,b = 99; 　　

不过，由于数据在计算机中的表示，最终以二进制的形式存在，所以有时候使用二进制，可以更直观地解决 问题。但二进制数太长了。比如int 类型占用4个字节，32位。比如100，用int类型的二进制数表达将是： 　　

0000 0000 0000 0000 0110 0100 　　

面对这么长的数进行思考或操作，没有人会喜欢。因此，用16进制或8进制可以解决这个问题。因为，进制越大，数的表达长度也就越短。

参考资料：

百度百科--二进制

参考技术A

1、十进制转二进制

方法为：十进制数除2取余法，即十进制数除2，余数为权位上的数，得到的商值继续除2，依此步骤继续向下运算直到商为0为止。

2、二进制转十进制

方法为：把二进制数按权展开、相加即得十进制数。

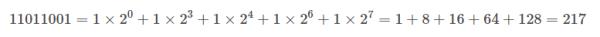
3、二进制转八进制

方法为：3位二进制数按权展开相加得到1位八进制数。（注意事项，3位二进制转成八进制是从右到左开始转换，不足时补0）。

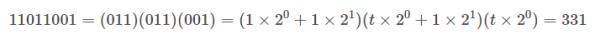
4、八进制转二进制

方法为：八进制数每个位上的数分别转换为三位二进制，顺序从右往左

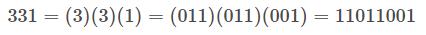
5、二进制转十六进制

方法为：与二进制转八进制方法近似，八进制是取三合一，十六进制是取四合一。（注意事项，4位二进制转成十六进制是从右到左开始转换，不足时补0）。

6、十六进制转二进制

方法为：十六进制数每个位上的数分别转换为四位二进制，顺序从右往左。

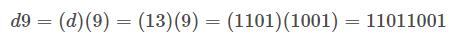
拓展资料：

由于计算机内只有高低电平，只能代表0和1两种状态，就此产生了二进制，而人们习惯的数字是十进制。所以就存在十进制与二进制之间的转换，但是由于二进制表示数据起来不方面（特别是当数值比较大时），十进制转换为二进制又比较麻烦，就产生了八进制、十六进制。

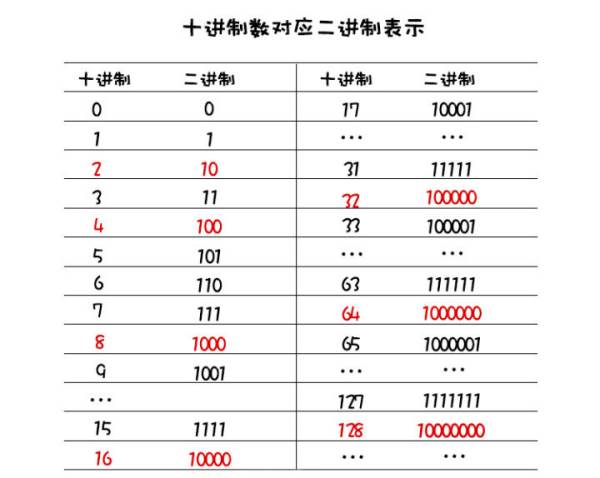
十进制对应二进制的表示：

进制，Octal，缩写OCT或O，一种以8为基数的计数法，采用0，1，2，3，4，5，6，7八个数字，逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。八进制的数和二进制数可以按位对应（八进制一位对应二进制三位），因此常应用在计算机语言中。

参考资料：二进制_百度百科，八进制_百度百科

参考技术B 进制转换之间，从较大的进制转为较小的进制，最基本的运算方式是除n反余法。

十进制转二进制：除2反余法。
例如十进制的10转为2进制，过程如下：
10 ÷ 2 = 5……0
5 ÷ 2 = 2……1
2 ÷ 2 = 1……0
1 ÷ 2 = 0……1
转换结果为1010。
十进制转八进制、十六进制，也可以采用除8/16反余法。

二进制转十进制：各阶累加法。
例如二进制的110101转为十进制，过程如下：
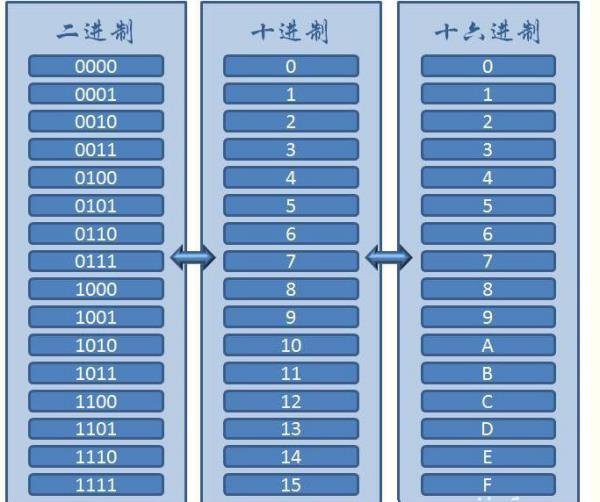
1×2^5 + 1×2^4 + 0×2^3 + 1×2^2 + 0×2^1 + 1×2^0 = 32 + 16 + 0 + 4 + 0 + 1 = 53
八进制、十六进制转十进制也是类似。例如十六进制的FEDC转为十进制，过程如下：
15×16^3 + 14×16^2 + 13×16^1 + 12×16^0 = 61440 + 3584 + 208 + 12 = 65244

进制之间如果有幂关系则可以快速转换。例如二进制转八进制、十六进制就可以快速换算。
由于8 = 2^3，因此二进制的连续三位可直接换算为八进制的一位。高位不足的补0。
例如二进制的10101100从最低位开始每3位分隔，可表示为 010 101 100，也就是八进制的254。
十六进制与之雷同。
八进制、十六进制转二进制也可以进行反向的快速运算。 参考技术C 不同进位计数制之间的转换原则：不同进位计数制之间的转换是根据两个有理数如相等，则两数的整数和分数部分一定分别相等的原则进行的。也就是说，若转换前两数相等，转换后仍必须相等。
有四进制
十进制：有10个基数：0
~~
9
，逢十进一
二进制：有2
个基数：0
~~
1
，逢二进一
八进制：有8个基数：0
~~
7
，逢八进一
十六进制：有16个基数：0
~~
9，A，B，C，D，E，F
(A=10,B=11,C=12,D=13,E=14,F=15)
，逢十六进一
1.十进制转换成二进制：十进制整数转换成二进制整数通常采用除2取余法，小数部分乘2取整法。例如，将(30)10转换成二进制数。
将(30)10转换成二进制数
2|
30
….0
----最右位
2
15
….1
2
7
….1
2
3
….1
1
….1
----最左位
∴
(30)10=（11110)2
将(30)10转换成八、十六进制数
8|
30
……6
------最右位
3
------最左位
∴
(30)10
=(36)8
16|
30
…14(E)----最右位
1
----最左位
∴
（30)10
=（1E)16
2、将P进制数转换为十进制数
把一个二进制转换成十进制采用方法：把这个二进制的最后一位乘上20，倒数第二位乘上21，……,一直到最高位乘上2n,然后将各项乘积相加的结果就它的十进制表达式。
把二进制11110转换为十进制
（11110）2=1*24+1*23+1*22+1*21+0*20=
=16+8+4+2+0
=（30）10
把一个八进制转换成十进制采用方法：把这个八进制的最后一位乘上80，倒数第二位乘上81，……,一直到最高位乘上8n,然后将各项乘积相加的结果就它的十进制表达式。
把八进制36转换为十进制
（36）8=3*81+6*80=24+6=（30）10
把一个十六进制转换成十进制采用方法：把这个十六进制的最后一位乘上160，倒数第二位乘上161，……,一直到最高位乘上16n,然后将各项乘积相加的结果就它的十进制表达式。
把十六制1E转换为十进制
（1E）16=1*161+14*160=16+14=（30）10
3、二进制转换成八进制数
(1)二进制数转换成八进制数：对于整数，从低位到高位将二进制数的每三位分为一组，若不够三位时，在高位左面添0，补足三位，然后将每三位二进制数用一位八进制数替换，小数部分从小数点开始，自左向右每三位一组进行转换即可完成。例如：
将二进制数1101001转换成八进制数，则
(001
101
001)2
|
|
|
(
1
5
1)8
(
1101001)2=(151)8
4.八进制数转换成二进制数：只要将每位八进制数用三位二进制数替换，即可完成转换，例如，把八进制数(643.503)8，转换成二进制数，则
(6
4
3
.
5
0
3)8
|
|
|
|
|
|
(110
100
011
.
101
000
011)2
(643.503)8=(110100011.101000011)2
5、二进制与十六进制之间的转换
(1)二进制数转换成十六进制数：由于2的4次方=16，所以依照二进制与八进制的转换方法，将二进制数的每四位用一个十六进制数码来表示，整数部分以小数点为界点从右往左每四位一组转换，小数部分从小数点开始自左向右每四位一组进行转换。
(2)十六进制转换成二进制数
如将十六进制数转换成二进制数，只要将每一位十六进制数用四位相应的二进制数表示，即可完成转换。
例如：将(163.5B)16转换成二进制数，则
(
1
6
3
.
5
B
)16
|
|
|
|
|
(0001
0110
0011.
0101
1011
)2
(163.5B)16=(101100011.01011011)2 参考技术D n进制转化为十进制，都是一个方法，就是：
n进制的个位数× n的0次方+n进制的十位数× n的1次方+n进制的百位数×n的2次方+……
例如：（101101）2=1× 2的5次方+0× 2的4次方+1× 2的3次方+1× 2的2次方+0× 2的1一次方+1× 2的0次方=32+0+8+4+0+1=45
（131）8=1× 8的2次方+3× 8的1次方+1× 8的0次方=64+24+1=89
（5A）16=5× 16的1次方+10× 16的0次方=80+10=90

十进制转化为n进制，也都是一个方法，就是：取余法
比如十进制的89转化为二进制
89除以2得44……余1
44除以2得22……余0
22除以2得11……余0
11除以2得5……余1
5除以2得2……余1
2除以2得1……余0
1除以2得0……余1 (必须除到得数是0为止)

看余数，从下数到上，得(1011001)2

转化为八进制，十六进制，同上，除以8,或16就行。

二进制转化为八进制、十六进制：
例如：
（1101010110）2
转化为八进制，就是，（1 101 010 110）2 ，三位数一组，从个位数数起的，相对应的八进制就是1 5 2 6
转化为十六进制，就是，四位一组，同上。

八进制、十六进制转化为二进制
同上，直接反过来就行。

字节怎么转换成二进制？

求解说

参考技术A 这种说法本身是错误的。
二进制是一种数的表示方法；
而字节是计算机中的存储单位；
二者并没有所谓的转换机制。 参考技术B 字节本来就是二进制啊
1个字节是由8个二进制数组成的 参考技术C 首先，字节是单位，可以说是8bit。我知道你想问的，但在这我解释不清，这个问题的关键在编码上，建议你把进制问题和编码问题看一下，你的疑问就可以解决了 参考技术D 有点不明白你的意思，
二进制是一种数的表示方法，
字节是计算机中的存储单位。 第5个回答  2017-05-22 VC调试(TC或BC用TD调试)时按Alt+8、Alt+6和Alt+5,打开汇编窗口、内存窗口和寄存器窗口看每句C对应的汇编、单步执行并观察相应内存和寄存器变化，这样过一遍不就啥都明白了吗。
对VC来说，所谓‘调试时’就是编译连接通过以后，按F10或F11键单步执行一步以后的时候，或者在某行按F9设了断点后按F5执行停在该断点处的时候。
（Linux或Unix下可以在用GDB调试时,看每句C对应的汇编并单步执行观察相应内存和寄存器变化。）
想要从本质上理解C指针，必须学习汇编以及C和汇编的对应关系。
从汇编的角度理解和学习C语言的指针，原本看似复杂的东西就会变得非常简单！
指针即地址。“地址又是啥？”“只能从汇编语言和计算机组成原理的角度去解释了。”