浮点数的十六进制表示

Posted 2023-05-12

参考技术A IEEE 754规定了表示浮点数值的方式：单精确度（32位元）、双精确度（64位元），

单精度二进制小数，使用32个位元存储，

其中分为符号位（S）, 指数位（Exp）,有效数位（Fraction）

【从左到右依次排序分别位1位、8位、23位】

指数部分即使用所谓的偏正值形式表示，实际值为表示值与一个固定值（32位的情况是127）的和。

例如有一个浮点数是6.91，如何将其转换为十六进制呢？

首先将6.91转换为二进制形式：

110.111010001111010111000

将其规范化：调整使其实数第一位大于1小于2

6.91 = 1.10111010001111010111000 * 2^2

基本原型出来了

S：0

EXP : 2+127(10进制) =129(10进制) = 10000001(2进制)

Fraction : 10111010001111010111000 （注意：小数点前面的1不要了）

组合一下： 0 10000001 10111010001111010111000
= 0100 0000 1101 1101 0001 1110 1011 1000
= 4 0 D D 1 E B 8

原文： https://blog.csdn.net/Cheatscat/article/details/78533349

（十六）浮点数和定点数

一、浮点数不精确性

在自算计中打开python命令行输入0.3+0.6我们可以看到输出结果是0.899999，出现这种结果和计算机中对于浮点数的保存方法有关。

二、定点数的表达

        假如我们使用四个字节表示一个0~9的整数，32位就可以保存8个这样的整数，使用左边的6个表示整数位，右边两个表示小数位，这样就可以表示0~999999.99范围的数，总共有一亿个，这就是BCD编码。这种编码方式的缺陷也很明显：

1. 浪费，32位本可以表示2^32个数字；
2. 表示范围极其有限；

三、浮点数制表示

        计算机中实际对于浮点数的表示采用科学计数法，细节如下：

1. 第一位表示符号位，0为正1为负。为s
2. 2~9位为指数位，8位可以表示0~255，这里将1~254其映射到-126~127。为e
3. 其余23位为有效数位。为f

        其所表示的数为 (-1)^s*1.f*2^e，除此之外有一些特殊表示：

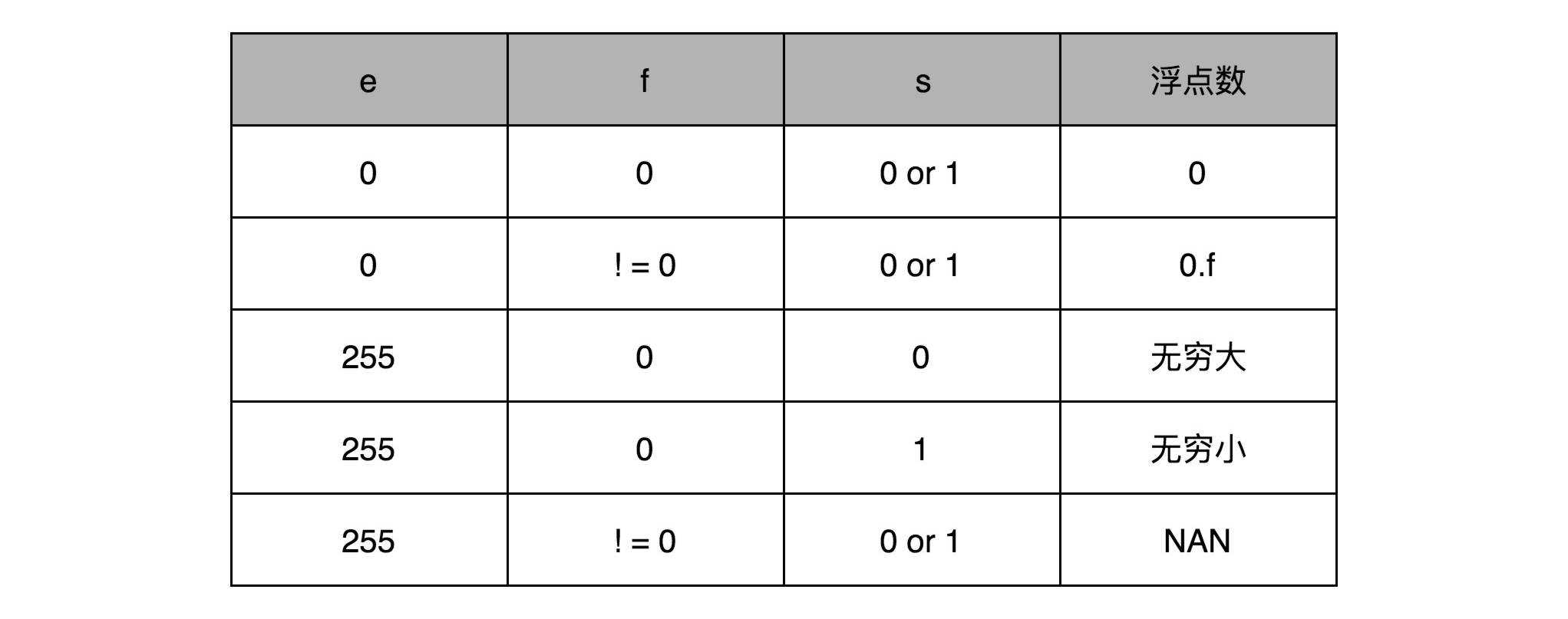
        例如0.5表示如下：

　　 

        由于指数位用1~254表示 -126~127，所以-1就是1~254的第126个数

四、浮点数的二进制转化

        十进制小数转为二进制小数方法是指数位用除2取余法；小数位则不断乘以2，如乘2的结果大于1则当前位取1，如小于1则当前位取0，继续乘以2，不断重复这个过程，直至乘的结果为1：

         

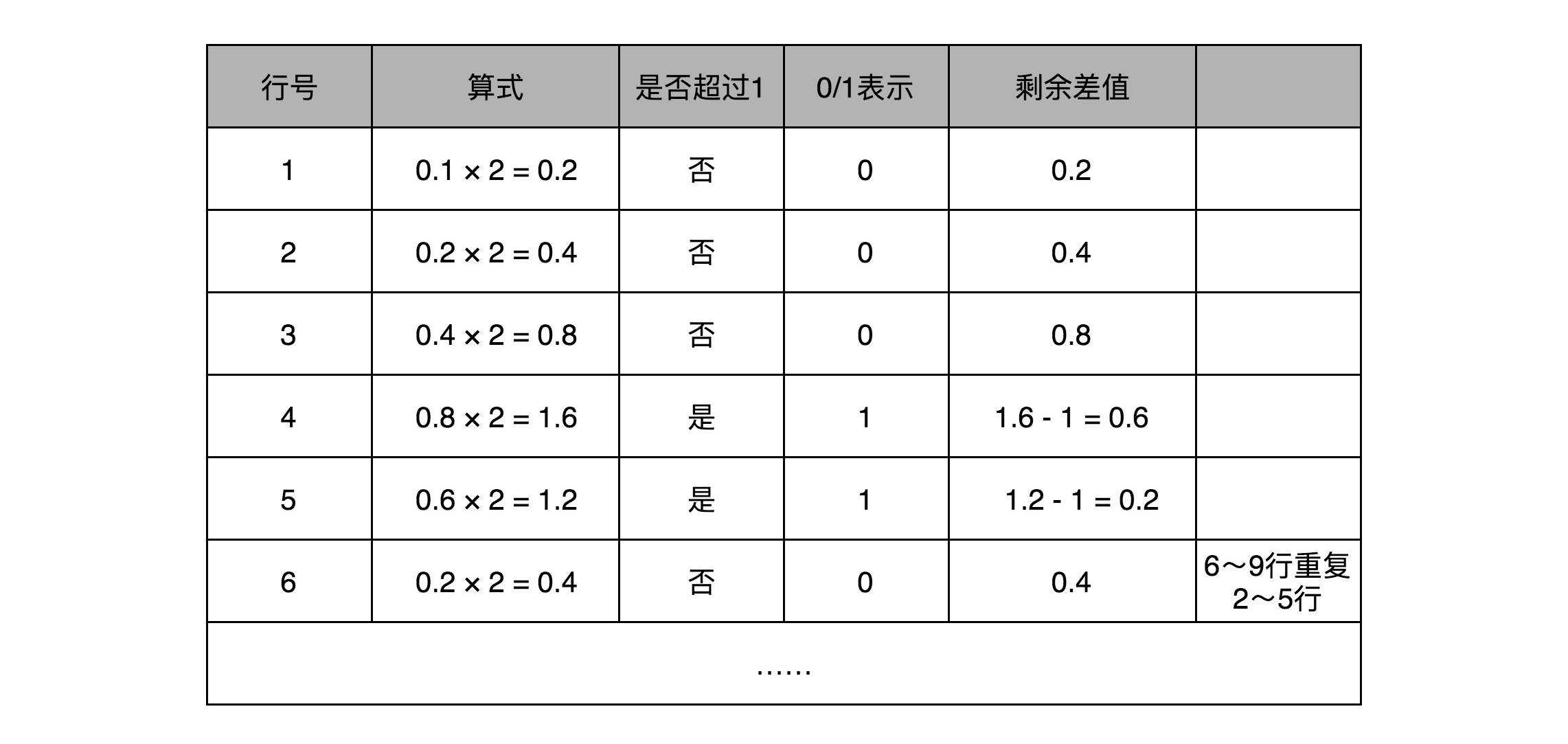
        十进制数9.1转为二进制，需要将整数位与小数位分开处理，整数位为1001，小数位如下，是一个无限循环小数0.000110011……，因此表示为1001.000110011……，左移三位表示为1.001000110011……

由于有效位只有23位，后面的会被截掉，最终表示结果为：

        将这个数转为十进制，准确结果为：9.09999942779541015625，这也就是浮点数表示法中精度损失的原因。

五、浮点数加法和精度损失

        浮点数的加法原则是六个字：先对齐，再计算；就是先将两个数的指数位转换成一致，就是把指数位较小的数右移之后再对齐，再计算有效位即可。例如十进制的0.5+0.125计算过程如下：

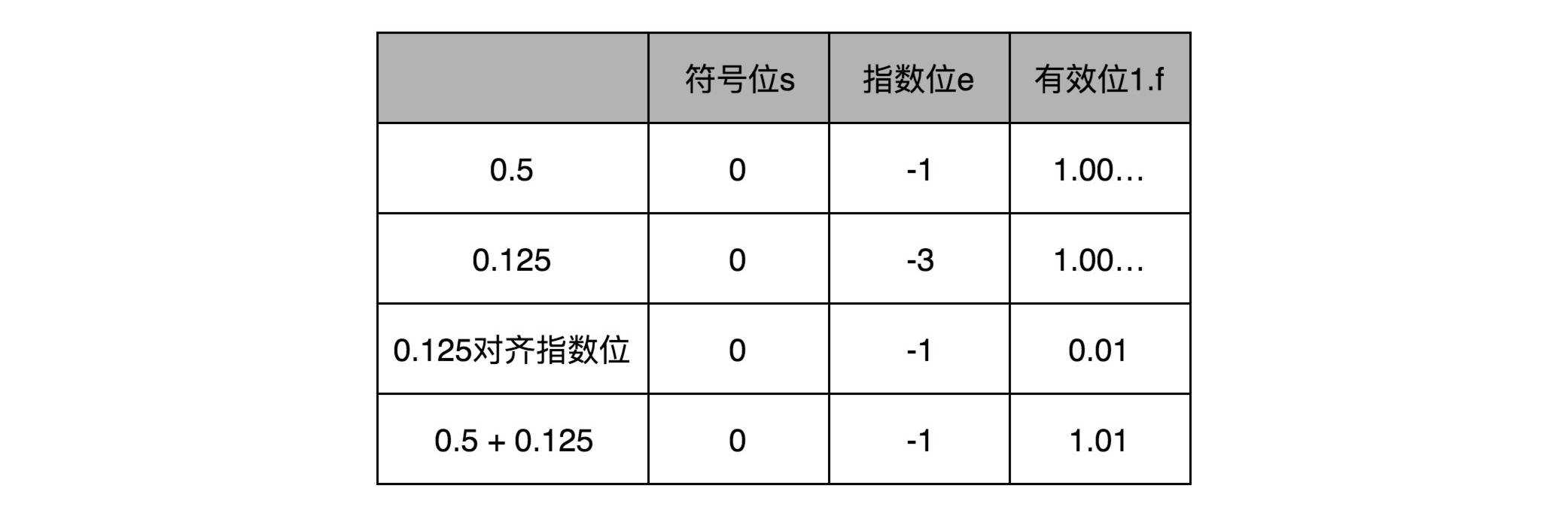
        在这个过程中我们发现在对齐操作中，有些数字的有效位会由于位移丢失，因此损失了精度。两个数相差越大则=对齐操作中损失精度的可能性越大，32位数有效位长23位，这就意味着如果两个数相差2^24倍（大概1600万倍），则两个数相加结果不会改变。

六、Kahan Summation 算法

        上面精度损失的例子中，假若我们连续加2000万次较小的那个数，计算结果还是不会变化，但实际值增加一倍多，在这种“积少成多”的情况下，误差就太大了，在机器学习的计算场景下这种情况尤其多。解决这个问题的办法就是科学家提出的Kahan Summation算法，这种方式计算2000万个1.0f相加的过程如下：

public class KahanSummation {
  public static void main(String[] args) {
    float sum = 0.0f;
    float c = 0.0f;
    for (int i = 0; i < 20000000; i++) {
      float x = 1.0f;
      float y = x - c;
      // 求和，需要使用sum值加1.0再加上上一步的精度损失c，主要是这个加法造成了进度损失。
      float t = sum + y;
      // 这一步拆分为两步，t和sum相差较小，t-sum的结果和y也非常接近，因此这一步精度损失几乎为0
　　　 c = (t-sum)-y;
      sum = t;      
    }
    System.out.println("sum is " + sum);   
  }  
}

        实质是，每次计算时都使用一次减法（c=(t-sum)-y）将损失精度记录下来，下次相加时再补足（x=1.0f,y=x-c）