[leetcode] 面试题 17.20. 连续中值 | 对顶堆维护动态中位数

Posted 2023-02-18 PushyTao

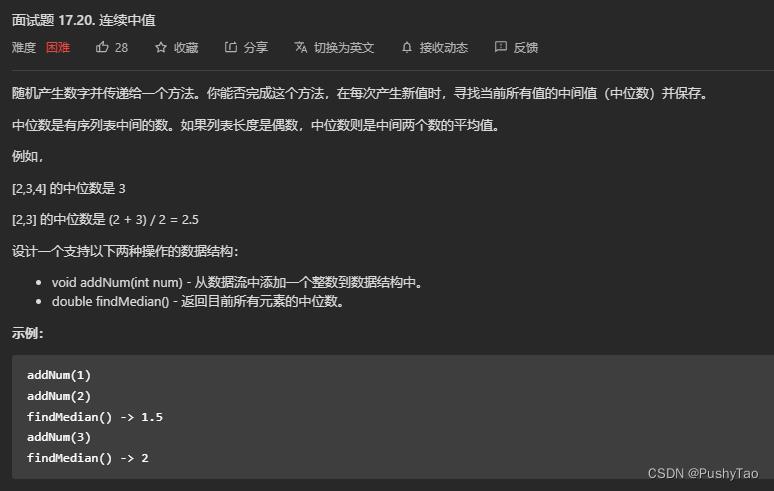
有很多种形式可以实现中位数的求解，比如将所有的数放到一个数组中，然后sort一下获取中间的值，但这样在时间复杂度上不太优雅；为了能够更快的求解，可以使用对顶堆来求解。
对顶堆通常用来实现动态k大（小）的问题。在这个题里，因为在往里面加数的过程中，数的总数量cnt是在不断加大的，所以说第（cnt+1）/2大也是在不断变化的，正好符合对顶堆的应用场景。

想要了解对顶堆求解第k大可以看博主的另一个博客：传送门

由大根堆和小根堆构成，小根堆在上，大根堆在下，两个堆的根相对，所以说就形成了一个有序的结构（xiao.top() >= da.top()）
放数据的时候，往小根堆中添加，然后维护它们之间size()的大小关系即可，比如：
当数的总量为奇数的时候，xiao.size() == da.size() + 1，当数的总量为偶数的时候，xiao.size() == da.size()

还要注意可能会出现xiao.top()<da.top()的情况，比如按照顺序push -1 -2 -3的过程会导致这样的情况，此时还要考虑xiao.top()和da.top()之间的大小关系，然后再处理一下（将大根堆的堆顶元素放入小根堆，然后将小根堆的堆顶元素放到大根堆）

ac_code:

class MedianFinder 
public:
    /** initialize your data structure here. */
    MedianFinder() 
        this->cnt = 0;
    
    
    void addNum(int num) 
        xiao.push(num);
        cnt ++;
        while(xiao.size() > da.size() + 1) 
            da.push(xiao.top());
            xiao.pop();
        
        if(xiao.size() && da.size() && (xiao.top() < da.top())) 
            xiao.push(da.top());
            da.pop();
        
        while(xiao.size() > da.size() + 1) 
            da.push(xiao.top());
            xiao.pop();
        
    
    
    double findMedian() 
        // std::cout << cnt << std::endl;
        // std::cout << xiao.top() << " " << xiao.size() << std::endl;
        // std::cout << da.top() << " " << da.size() << std::endl;
        if(xiao.size() == da.size() + 1) return 1.0 * xiao.top();
        else return 1.0 * ((xiao.top() + da.top()) / 2.0);
    
private:
    std::priority_queue<int,std::vector<int>, std::greater<int> >xiao;
    std::priority_queue<int,std::vector<int>, std::less<int> >da;
    int cnt;
;

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */