如何区分条件概率、乘法公式、全概率公式和贝叶斯公式?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何区分条件概率、乘法公式、全概率公式和贝叶斯公式?相关的知识,希望对你有一定的参考价值。
本人在学习自考的《概率论与数理统计(经管类)》,希望能有高人指点迷津~~最好能提供一点公式及定义总结的资料,通俗易懂的举例更好!
条件概率用在A 事件发生的情况下B事件发生的概率。
概率乘法公式用在AB 同时发生时候。
全概率公式用在A事件可以看作整体被B分割时候。
贝叶斯公式用于先验和后验 较复杂精确时用边际分布密度
扩展资料:
条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为:P(A|B),读作“在B的条件下A的概率”。
概率乘法公式又称乘法定理.关于事件积的概率的重要定理.若P(A)>O,P(BWO)
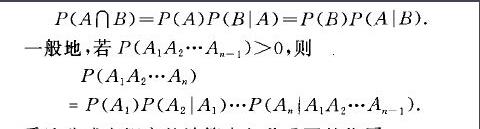
全概率公式是将对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题。
内容:如果事件B1、B2、B3…Bn 构成一个完备事件组,即它们两两互不相容,其和为全集;并且P(Bi)大于0,则对任一事件A有
P(A)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn)。
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。

参考资料:条件概率-百度百科 概率乘法公式-百度百科 全概率公式=百度百科 贝叶斯公式-百度百科
全概率公式和贝叶斯公式相对而言比较复杂,但也是在条件概率公式的基础上作推导得出的
之所以这么解释只是希望楼主对这几个公式有个大概的认识,楼主可以直接买本《概率论与数理统计》大学用的那种,你所想要的都有,一看就可以懂得,希望对你有所帮助本回答被提问者采纳 参考技术B 例如两事件不独立互排斥的情况
条件概率 P(B/A)=P(AB)/P(A) P(A)不等于0
A 事件发生的情况下B事件发生的概率
乘法公式 P(AB)=P(A)P(B/A)=P(B)P(A/B)
AB 同时发生时候计算方法
全概率公式 P(A)=P(B)P(A/B)+P(-B)P(A/-B)
A事件可以看作整体 被B分割 时候计算方法
贝叶斯公式 P(B/A)=P(B)P(A/B) / ( P(B)P(A/B)+P(-B)P(A/-B) )
在条件和全概率的基础上的变形
用途很广 主要用于先验和后验 较复杂精确时用边际分布密度
以上适合较多事件 A1,An,B1.Bn
公式就变成和的形式 参考技术C 全概率公式:由因求果
贝叶斯公式:由果求因 参考技术D 看看书好了,这个东东我也快考了。。。
徒手打造一个朴素贝叶斯分类器
开篇
正如其名,"朴素贝叶斯"原理"朴素",实现简单,是一种常用的机器学习算法。
为何“朴素”?如何训练?如何分类?如何实现?别急,咱们慢慢道来~
概率统计回忆录
朴素贝叶斯也是贝叶斯方法的一种,提起贝叶斯,学过概率统计的你一定听说过条件概率公式,全概率公式和贝叶斯公式吧,忘记了也没关系,我们先来快速过一遍。
条件概率公式:
全概率公式:
贝叶斯公式:
可以发现,贝叶斯公式其实就是由条件概率公式和全概率公式推导的,贝叶斯公式的分母是一个全概率公式,分子是一个条件概率公式。
后续的推导将会用到上面的公式。
朴素贝叶斯的训练(学习)方法
朴素贝叶斯在使用训练数据进行“学习”时,其实是在学习数据的生成机制,具体点,是在学习特征 与标签 的联合概率分布 。
再进一步解释:根据条件概率公式, ,所以朴素贝叶斯要学习联合概率分布 ,就需要学习 以及 ,而这两项完全可以从训练集中学到,于是整个朴素贝叶斯的学习之路就“几乎”被打通啦
之所以用“几乎”,是因为以上过程还存在一个问题:
在 中, 是类别标签,假设共 类; 是特征,假设共 个特征 ,且 的可能取值共 个, ,那么对于每一个类别标签 , 的不同组合总数达到了 ,于是 总共需要计算 个参数。当每个特征的不同取值较多时,计算开销会特别大,这在实际应用中是不可行的。
那应该怎么办呢?
可以假设 是条件独立的!具体来说就是 满足下面的公式:
此时,对于每一个类别标签 ,都对应需要计算 次(第 个特征共有 个不同取值),
那么 个类别标签与 个特征的全部不同组合数为 ,也就是说 总共需要计算 个参数。
当每个特征的不同取值较多时, 将会远小于 ,这样的计算量是可以接受的。
朴素贝叶斯正式基于这一条件独立性假设!
由于这个假设在现实生活中几乎不能被满足,因此说该算法是“朴素”的,这也正是朴素贝叶斯的得名由来。
这样,朴素贝叶斯的学习之路彻底被打通啦!
朴素贝叶斯分类器
上一节介绍了朴素贝叶斯如何利用训练数据进行学习,当学习完成之后,如何做分类呢?让我们来推导一下吧。
在进行分类时,对于给定的样本特征 ,朴素贝叶斯分类器会将所有可能的类别作为备选答案,然后分别计算在给定特征的条件下,样本被判定为某类别的概率,最后比较一下这些概率的大小,最大概率对应的的类别就是朴素贝叶斯分类器最终的分类结果。
以上所计算的概率,被称为后验概率,用贝叶斯公式描述如下:
前面我们已经利用条件独立性得到
将它代入刚刚推导的 中,得到
在上式中,分母对于每一个 都是相同的,因此可以不考虑分母,于是朴素贝叶斯分类器最终的分类结果是 中最大值对应的类别。
极大似然法估计参数
我们已经讲解了朴素贝叶斯如何利用训练集进行学习(训练),以及如何用学习(训练)好的模型做分类。
但有一个问题还没有解决:我们只是明确了“学习意味着估计 和,并且这两项完全可以从训练集中学到”,但是具体如何“学习”(估计这些参数)呢?
这里使用极大似然法进行学习(参数的估计)。
被称为先验概率,它的极大似然估计为:
其中 为样本个数。
设第 个特征所有可能的取值集合为 ,则 的极大似然估计为:
其中, 为指示函数特征总数为 ,第 个特征共 个不同取值,总共有 个不同类别。
案例实战
训练集如下,希望学习一个朴素贝叶斯分类器,对新的样本 进行分类。
根据上面的推导,我们需要计算
总类别数; 总特征数
待分类的样本 的类别就是集合中最大值对应的类别
使用训练集进行训练,需要计算 个先验概率和 个条件概率:
这样就学习完成并得到了一个朴素贝叶斯分类器,接下来开始做分类了。
对于给定的新样本 ,计算:
因为后者较大,所以朴素贝叶斯将会把新样本 归到 类中。
Python实现朴素贝叶斯分类器
本小节将用Python实现一个朴素贝叶斯分类器。
我们依然使用上一节栗子中的数据(后台回复"bayes_data"可获取数据)来测试分类器,先读取进来看一下:
data=pd.read_csv('bayes_data.csv')
print(data)
输出:
fea1 fea2 label
0 1 S -1
1 1 M -1
2 1 M 1
3 1 S 1
4 1 S -1
5 2 S -1
6 2 M -1
7 2 M 1
8 2 L 1
9 2 L 1
10 3 L 1
11 3 M 1
12 3 M 1
13 3 L 1
14 3 L -1
现在来实现朴素贝叶斯分类器
class Bayes():
pass
整体的思路是:
对于待分类的样本 :
计算先验概率
计算条件概率
根据上面二式计算,并取其中最大值对应的 作为样本 的类别。
所以我们可以先定义两个方法,分别计算先验概率和条件概率
#计算先验概率
def cal_prior_prob(self,class_list):
pass
#计算给定类别的条件下,每个特征取不同值的概率
def cal_cond_prob(self,dataset):
pass
cal_prior_prob比较容易实现,只需对类别列统计一下不同取值的个数,然后除以总样本数。注意到“统计某列不同取值的个数”这一操作在后面会被多次使用,因此先把它写成一个单独的方法:
#统计某一列不同取值及其对应个数
def value_count(self,lis):
dic={}#统计lis中不同取值个数
for i in lis:
if i in dic.keys():
dic[i]+=1
else:
dic[i]=1
res=[]
for i in dic.keys():
res.append((i,dic[i]))
return res#二元组组成的列表
然后就可以实现cal_prior_prob了:
#计算先验概率
def cal_prior_prob(self,class_list):
res=self.value_count(class_list)#统计类别列中不同取值及其对应个数
prior_prob=[]
for item in res:
prior_prob.append((item[0],item[1]/len(class_list)))
return prior_prob
cal_cond_prob的实现稍微有些复杂。由于需要计算类别标签取不同值的条件下一系列的概率,因此需要按照类别标签的不同将数据集做划分,我们先来实现数据集划分函数:
#获取不同类别标签下对应的子集
def split_dataset(self,dataset,fea_index,value):
subset=[]#存储子集
n_samples=len(dataset.iloc[:,0])#样本量
#遍历数据集中每一个样本
for i in range(n_samples):
sample=list(dataset.iloc[i,:])
if sample[fea_index]==value:
subset.append(sample)
subset=pd.DataFrame(subset)
subset.columns=dataset.columns#设置子集列名
return subset
代码逻辑很清晰,不必多言。
还有个问题:应该如何存储这一堆计算得到的条件概率呢?
这里,我选择了嵌套的字典。具体的结构是这样的:
{1: {'fea1': {}, 'fea2': {}}, -1: {'fea1': {}, 'fea2': {}}}
最外层的1和-1代表两类标签;fea1和fea2代表2个特征,fea1对应的值(value)将会存储"第一个特征不同取值的个数/总样本数",即条件概率,fea2同理。
先搭建好这个框架,之后直接往对应位置填充数据即可。
有了以上铺垫,现在来实现cal_cond_prob:
#计算给定类别的条件下,每个特征取不同值的概率,并用字典存起来
def cal_cond_prob(self,dataset):
n_features=len(dataset.iloc[0,:])-1#总共有几个特征
#print(n_features)#2
class_list=dataset.iloc[:,-1]#全部类别
class_list_value=set(class_list)#类别的不同取值
dic={key:{} for key in class_list_value}#存储全部概率计算的结果,类似打表的方法
#先搭建好框架,后续直接往对应位置填充数据即可
for k in dic:
for i in range(n_features):
dic[k]['fea{}'.format(i+1)]={}
#print(dic)#{1: {'fea1': {}, 'fea2': {}}, -1: {'fea1': {}, 'fea2': {}}}
for label_value in class_list_value:#对于每一个类别label_value
subset=self.split_dataset(dataset,-1,label_value)#获取当前label_value对应的子集
#print(subset)#ok
for current_fea_index in range(n_features):#对于当前类别下的每一个特征
lis=subset.iloc[:,current_fea_index]#当前特征列
#print(lis)#ok
res=self.value_count(lis)#统计当前特征列中不同取值及其对应个数
#print(res)#ok
#当前特征不同取值占总数的比例,此即我们要求的条件概率
for item in res:
#计算比例,并写入字典中
dic[label_value]['fea{}'.format(current_fea_index+1)][item[0]]=item[1]/len(lis)
#print(dic)#ok
return dic
该方法最后返回的dic就存储了全部的条件概率。
完成以上任务后,可以使用我们的数据集测试一下:
if __name__ == "__main__":
dataset=pd.read_csv('bayes_data.csv')
class_list=dataset.iloc[:,-1]
bayes=Bayes()
#计算先验概率和条件概率
prior_prob=bayes.cal_prior_prob(class_list)#[(-1, 0.4), (1, 0.6)]
cond_prob=bayes.cal_cond_prob(dataset)
print('先验概率:{}\n\n条件概率:{}'.format(prior_prob,cond_prob))
输出:
先验概率:[(-1, 0.4), (1, 0.6)]
条件概率:{1: {'fea1': {1: 0.2222222222222222, 2: 0.3333333333333333, 3: 0.4444444444444444}, 'fea2': {'M': 0.4444444444444444, 'S': 0.1111111111111111, 'L': 0.4444444444444444}}, -1: {'fea1': {1: 0.5, 2: 0.3333333333333333, 3: 0.16666666666666666}, 'fea2': {'S': 0.5, 'M': 0.3333333333333333, 'L': 0.16666666666666666}}}
从输出结果可以得到先验概率为:
条件概率就没那么直观了,不过我们可以用在线工具https://www.bejson.com/explore/index_new/ 格式化一下:
将之前手算得到的的分数化成小数,与以上输出结果做个比较,你会发现,两者结果是一样的。这说明以上代码没有问题,测试通过。
有了这些用字典存储的条件概率,我们就可以用到哪个取哪个了。
现在“原料”俱齐,是时候实现最终的分类方法啦:
def judge(self,x,all_labels,prior_prob,cond_prob):
#尝试每一个类别
p=[]
for label,prob in prior_prob:
temp=prob
for i in range(len(x)):
temp*=cond_prob[label]['fea{}'.format(i+1)][x[i]]
p.append((label,temp))
#print(p)
return sorted(p,key=lambda x:x[1])[-1][0]
上述方法传入在本地计算好的先验概率、条件概率(字典格式)以及全部类别标签的不同取值,计算,最后排序并返回最大值对应的类别标签。
至此,整个朴素贝叶斯分类器就完成了。
试试看 会不会和我们之前手推的一样被归到-1类,代码如下
if __name__ == "__main__":
dataset=pd.read_csv('bayes_data.csv')
class_list=dataset.iloc[:,-1]
bayes=Bayes()
#计算先验概率和条件概率
prior_prob=bayes.cal_prior_prob(class_list)#[(-1, 0.4), (1, 0.6)]
cond_prob=bayes.cal_cond_prob(dataset)
all_labels=[i[0] for i in prior_prob]
x=(2,'S')
result=bayes.judge(x,all_labels,prior_prob,cond_prob)
print('分类结果为:',result)
输出:
分类结果为: -1
嗯,完全一致。
完整代码如下:
import pandas as pd
class Bayes():
#统计某一列不同取值及其对应个数
def value_count(self,lis):
dic={}#统计lis中不同取值个数
for i in lis:
if i in dic.keys():
dic[i]+=1
else:
dic[i]=1
res=[]
for i in dic.keys():
res.append((i,dic[i]))
return res#二元组组成的列表
#获取不同类别标签下对应的子集
def split_dataset(self,dataset,fea_index,value):
subset=[]#存储子集
n_samples=len(dataset.iloc[:,0])#样本量
#遍历数据集中每一个样本
for i in range(n_samples):
sample=list(dataset.iloc[i,:])
if sample[fea_index]==value:
subset.append(sample)
subset=pd.DataFrame(subset)
subset.columns=dataset.columns#设置子集列名
return subset
#计算先验概率
def cal_prior_prob(self,class_list):
res=self.value_count(class_list)#统计类别列中不同取值及其对应个数
prior_prob=[]
for item in res:
prior_prob.append((item[0],item[1]/len(class_list)))
return prior_prob
#计算给定类别的条件下,每个特征取不同值的概率,并用字典存起来
def cal_cond_prob(self,dataset):
n_features=len(dataset.iloc[0,:])-1#总共有几个特征
#print(n_features)#2
class_list=dataset.iloc[:,-1]#全部类别
class_list_value=set(class_list)#类别的不同取值
dic={key:{} for key in class_list_value}#存储全部概率计算的结果,类似打表的方法
#先搭建好框架,后续直接往对应位置填充数据即可
for k in dic:
for i in range(n_features):
dic[k]['fea{}'.format(i+1)]={}
#print(dic)#{1: {'fea1': {}, 'fea2': {}}, -1: {'fea1': {}, 'fea2': {}}}
for label_value in class_list_value:#对于每一个类别label_value
subset=self.split_dataset(dataset,-1,label_value)#获取当前label_value对应的子集
#print(subset)#ok
for current_fea_index in range(n_features):#对于当前类别下的每一个特征
lis=subset.iloc[:,current_fea_index]#当前特征列
#print(lis)#ok
res=self.value_count(lis)#统计当前特征列中不同取值及其对应个数
#print(res)#ok
#当前特征不同取值占总数的比例,此即我们要求的条件概率
for item in res:
#计算比例,并写入字典中
dic[label_value]['fea{}'.format(current_fea_index+1)][item[0]]=item[1]/len(lis)
#print(dic)#ok
return dic
def judge(self,x,all_labels,prior_prob,cond_prob):
#尝试每一个类别
p=[]
for label,prob in prior_prob:
temp=prob
for i in range(len(x)):
temp*=cond_prob[label]['fea{}'.format(i+1)][x[i]]
p.append((label,temp))
#print(p)
return sorted(p,key=lambda x:x[1])[-1][0]
if __name__ == "__main__":
dataset=pd.read_csv('bayes_data.csv')
class_list=dataset.iloc[:,-1]
bayes=Bayes()
#print(bayes.value_count(class_list))#[(-1, 6), (1, 9)]
#计算先验概率和条件概率
prior_prob=bayes.cal_prior_prob(class_list)#[(-1, 0.4), (1, 0.6)]
cond_prob=bayes.cal_cond_prob(dataset)
all_labels=[i[0] for i in prior_prob]
#print('先验概率:{}\n\n条件概率:{}'.format(prior_prob,cond_prob))
x=(2,'S')
result=bayes.judge(x,all_labels,prior_prob,cond_prob)
print('分类结果为:',result)
总结一下
本文讲解了朴素贝叶斯的由来,学习过程以及分类器的原理,并结合案例加以说明,最后用Python实现了一个基于极大似然估计的朴素贝叶斯分类器。
参考:
-
[1][统计学习方法]
最最后,原创不易,在看一下好不好
对了,南极Python交流群已经成立,欢迎入群学习交流(划水)
推 荐 阅 读
以上是关于如何区分条件概率、乘法公式、全概率公式和贝叶斯公式?的主要内容,如果未能解决你的问题,请参考以下文章