leetcode--03.位于同一条直线上点最大个数

Posted 2023-05-06

参考技术A

题目：
Given n points on a 2D plane, find the maximum number of points that lie on the same straight line
给定二维平面上的n个点，求出位于同一直线上的点的最大个数

思路：
相同的点算多个，这一点也是醉了
斜率无限大情况和相同点的情况要考虑到
还有map中的key，-0和+0算两个key
以及浮点数的精度问题

暂定这样，以后会回来修改，思路有，实现起来太恶心，还有牛客的测试用例和leetcode不一样

霍夫变换

• 霍夫检测-直线

　　前提条件 – 边缘检测已经完成，霍夫变换解决平面空间到极坐标空间转换。

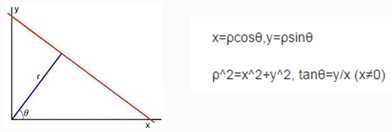
　　从霍夫空间曲线图来看，取不同的像素点都汇聚在一个点，这表明这些个像素点都属于同一条直线。（x_i,y_i）.对于任意一条直线上的所有点来说变换到极坐标中，从[0~360]空间，可以得到r的大小属于同一条直线上点在极坐标空(r, θ)必然在一个点上有最强的信号出现（如上图），根据此反算到平面坐标中就可以得到直线上各点的像素坐标。从而得到直线。

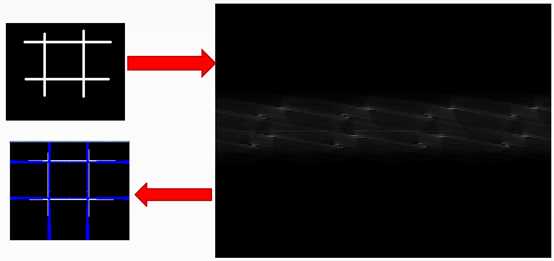
　　下图第一张为原图，第二张为提取边缘，第三张为直线检测并绘制。

• 霍夫检测-圆

　　极坐标变换原理：

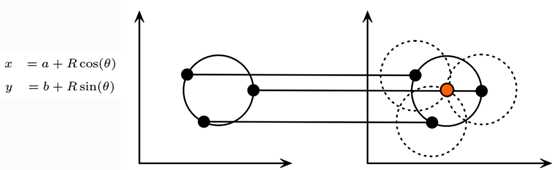
　　从平面坐标到极坐标转换三个参数C（x₀,y₀,r）其中(x₀,y₀)是圆心假设平面坐标的任意一个圆上的点，转换到极坐标中：C（x₀,y₀,r）处有最大值，霍夫变换正是利用这个原理实现圆的检测。

 　　霍夫圆检测对噪声比较敏感，所以首先要对图像做中值滤波。

 相关函数如下:

 1 //标准的霍夫变换HoughLines从平面坐标转换到霍夫空间，
 2 //最终输出是表示极坐标空间霍夫变换直线概率,要自己反变换到平面空间，一般不用; 
 3 HoughLinesP（int1，out1,）最终输出是直线的两个点（x1,y1，x2,y2）.
 4 
 5 霍夫直线检测HoughLinesP(out1,plinel,1,CV_PI/180.0,10,0,0);
 6 // out1为要检测的灰度图像，plinel 为输出的直线的两点，类型为vector<Vec4f>plinel;
 7 // 1为生成极坐标时候的像素扫描步长，CV_PI/180.0生成极坐标时候的角度步长，一般取值CV_PI/180，10为阈值，
 8 //只有获得足够交点的极坐标点才被看成是直线，最小直线长度0最大间隔0；
 9 for (size_t i=0;i<plinel.size();i++)
10 {
11 Vec4f hline = plinel[i];
12 line(out2, Point(hline[0], hline[1]),
13  Point(hline[2], hline[3]), 
14 colorf3, 3, 8);
15 }
16 
17 霍夫圆检测HoughCircles(out2, pcircle, CV_HOUGH_GRADIENT,1, 10, 100, 30,80,100); 
18 //out2为要检测的灰度图像，pcircle 为输出的圆心及半径，类型为vector<Vec3f>pcircle;    
19 //10 最短距离-可以分辨是两个圆的，否则认为是同心圆，30为中心点累加器阈值用于确定圆心80为最小半径100最大半径，
20 Mat dst = Mat(in1_image.size(), in1_image.type());    
21 for (size_t i=0;i< pcircle.size();i++)    
22 {        
23 Vec3f cc = pcircle[i];
24 circle(dst,Point(cc[0], cc[0]), cc[2], colorf3,2,LINE_AA);
25 circle(dst, Point(cc[0], cc[0]), 3, colorf, 2, LINE_AA);
26 }