冒泡排序算法有几种写法?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了冒泡排序算法有几种写法?相关的知识,希望对你有一定的参考价值。
冒泡排序算法有两种,一种是从大到小排,另一种是从小到大排。

冒泡排序依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。

冒泡排序最核心的思想就是相邻的两个元素相比较,符合冒泡的才冒泡,重复多次执行,待最后没有需要冒泡的元素时才停止执行,表示排序已经完成。
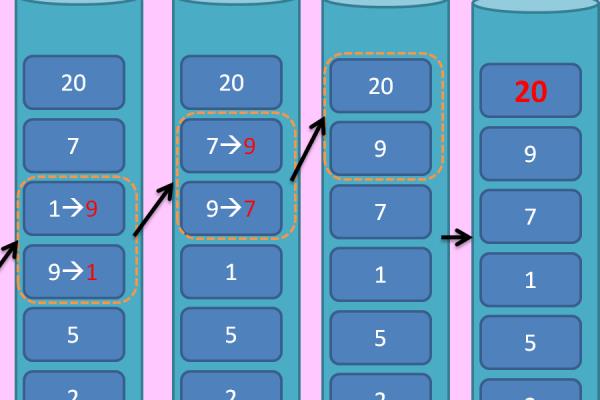
冒泡排序也是一种稳定排序算法。因为冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变。
参考技术A有两种写法。
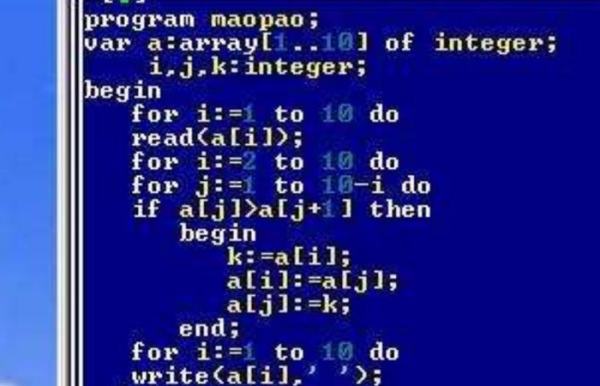
第一种思路:score[j] 和 score[j+1] 比较,如果前者比后者小,把前者和后者调换顺序,两两调换后一轮下来,最小的会被排到最后去。实现代码如下:

第二种思路:用 88 和 75 比较,再和69比较,再和 67 比较,发现88是最大的,把他排到第一位;然后 i=1,也就是第二轮,就不用看下标为 0 的 88 了。实现代码如下:

这就是冒泡排序的两种写法。
冒泡排序算法有2种。
它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端,故名。假设有一个大小为 N 的无序序列。冒泡排序就是要每趟排序过程中通过两两比较,找到第 i 个小(大)的元素,将其往上排。

假设有一个无序序列 12 35 99 18 76
思路:
1、先比较第 1 位和第 2 位的大小,12<35,因为希望越小越靠后,所以要调整两者顺序,交换后的结果:35 12 99 18 76
2、现在比较第 2 位和第 3 位的大小,12<99,所以需要交换位置,交换后的结果为:35 99 12 18 76
3、接着比较第 3 位和第 4 位的大小,12<18,交换后的结果为:35 99 18 12 76
4、最后比较第 4 位和第 5 位的大小,12<76,交换后的结果为:35 99 18 76 12
5、经过 4 次后我们发现 5 个数中最小的一个数已经就位,每将一个数归位我们称其为“一趟”
6、现在我们开始第二趟,目标将第 2 小的数归位,根据之前逻辑,还是从第 1 个数和第 2 个数开始比较上:35 99 18 76 12 --①--> 99 35 18 76 12 --②--> 99 35 18 76 12 --③--> 99 35 76 18 12,在第一趟比较就知道第 5 位是最小的,所以第 4 位不用和第 5 位比较,这一趟只需比较 3 次
7、第3趟:99 35 76 18 12 --> 99 35 76 18 12 --> 99 76 35 18 12 (比较 2 次)
8、第4趟:99 76 35 18 12 --> 99 76 35 18 12 ,有4个数已经就位,那么最后一个数无须比较,它就是最大的
总结: 如果有 n 个数进行排序,只需将 n-1 个数归位,即要进行 n-1 趟操作,而每一趟开始都从第 1 位进行相邻的两个数 进行比较,将小的那个数放在后面,已经归位的就不用进行比较。
参考技术C冒泡排序算法有2种写法。
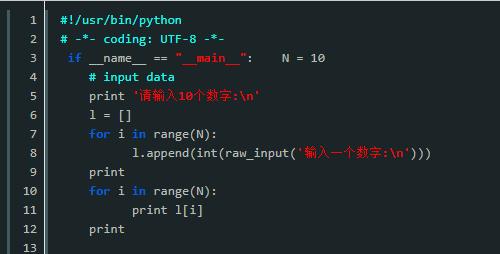
第一种思路:score[j] 和 score[j+1] 比较,如果前者比后者小,把前者和后者调换顺序,两两调换后一轮下来,最小的会被排到最后去。
第二种思路:用 88 和 75 比较,再和69比较,再和 67 比较,发现88是最大的,把他排到第一位;然后 i=1,也就是第二轮,就不用看下标为 0 的 88 了,因为他是老大,然后接着比较。
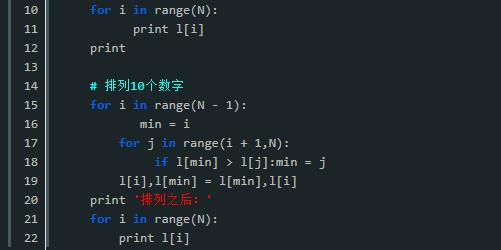
冒泡排序分从大到小和从小到大两种排序方式。它们的唯一区别就是两个数交换的条件不同,从大到小排序是前面的数比后面的小的时候交换,而从小到大排序是前面的数比后面的数大的时候交换。我这里只说 从小到大的排序方式。
冒泡排序的原理:从第一个数开始,依次往后比较,如果前面的数比后面的数大就交换,否则不作处理。这就类似烧开水时,壶底的水泡往上冒的过程。
每次把相邻的两个比较大小,然后把大一点儿的数据放在最后面,这样第一趟下来,最大的那个数就跑到了最后面,下一次排序就不用跟最后一个数字比较了,然后倒数第二大的数字会在倒数第二...因此可以使用两个函数,一个用于控制每一趟比较的元素个数,一个用于交换。
参考技术D有两种写法。
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。

所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。

冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。

它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
冒泡排序算法的原理如下:
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
排序算法突击(Java):冒泡排序
文章目录
冒泡排序
冒泡三种写法:
冒泡排序是入门级的算法,但也有一些有趣的玩法。通常来说,冒泡排序有三种写法:
- 一边比较一边向后两两交换,将最大值 / 最小值冒泡到最后一位;
- 经过优化的写法:使用一个变量记录当前轮次的比较是否发生过交换,如果没有发生交换表示已经有序,不再继续排序;
- 进一步优化的写法:除了使用变量记录当前轮次是否发生交换外,再使用一个变量记录上次发生交换的位置,下一轮排序时到达上次交换的位置就停止比较。
冒泡第一种写法:
public static void bubbleSort(int[] arr)
for (int i = 0; i < arr.length - 1; i++)
for (int j = 0; j < arr.length - 1 - i; j++)
if (arr[j] > arr[j + 1])
// 如果左边的数大于右边的数,则交换,保证右边的数字最大
swap(arr, j, j + 1);
// 交换元素
private static void swap(int[] arr, int i, int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
最外层的 for 循环每经过一轮,剩余数字中的最大值就会被移动到当前轮次的最后一位,中途也会有一些相邻的数字经过交换变得有序。总共比较次数是 (n-1)+(n-2)+(n-3)+…+1。
这种写法相当于相邻的数字两两比较,并且规定:“谁大谁站右边”。经过 n-1 轮,数字就从小到大排序完成了。整个过程看起来就像一个个气泡不断上浮,这也是“冒泡排序法”名字的由来。
添加主函数:
public static void main(String[] args)
int[] arr = 5,3,6,2,1,8,9,7,4;
Solution.bubbleSort(arr);
System.out.println(Arrays.toString(arr));
运行结果如下:

冒泡排序的第二种写法
第二种写法是在第一种写法的基础上改良而来的:
public static void bubbleSort(int[] arr)
// 初始时 swapped 为 true,否则排序过程无法启动
boolean swapped = true;
for (int i = 0; i < arr.length - 1; i++)
// 如果没有发生过交换,说明剩余部分已经有序,排序完成
if (!swapped)
break;
// 设置 swapped 为 false,如果发生交换,则将其置为 true
swapped = false;
for (int j = 0; j < arr.length - 1 - i; j++)
if (arr[j] > arr[j + 1])
// 如果左边的数大于右边的数,则交换,保证右边的数字最大
swap(arr, j, j + 1);
// 表示发生了交换
swapped = true;
// 交换元素
private static void swap(int[] arr, int i, int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
最外层的 for 循环每经过一轮,剩余数字中的最大值仍然是被移动到当前轮次的最后一位。这种写法相对于第一种写法的优点是:如果一轮比较中没有发生过交换,则立即停止排序,因为此时剩余数字一定已经有序了。
看下动图演示:
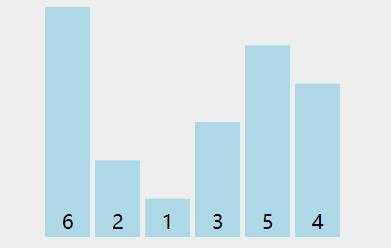
图中可以看出:
- 第一轮排序将数字 66 移动到最右边;
- 第二轮排序将数字 55 移动到最右边,同时中途将 11 和 22 排了序;
- 第三轮排序时,没有发生交换,表明排序已经完成,不再继续比较。
冒泡排序的第三种写法
第三种写法比较少见,它是在第二种写法的基础上进一步优化:
public static void bubbleSort(int[] arr)
boolean swapped = true;
// 最后一个没有经过排序的元素的下标
int indexOfLastUnsortedElement = arr.length - 1;
// 上次发生交换的位置
int swappedIndex = -1;
while (swapped)
swapped = false;
for (int i = 0; i < indexOfLastUnsortedElement; i++)
if (arr[i] > arr[i + 1])
// 如果左边的数大于右边的数,则交换,保证右边的数字最大
swap(arr, i, i + 1);
// 表示发生了交换
swapped = true;
// 更新交换的位置
swappedIndex = i;
// 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置
indexOfLastUnsortedElement = swappedIndex;
// 交换元素
private static void swap(int[] arr, int i, int j)
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
经过再一次的优化,代码看起来就稍微有点复杂了。最外层的 while 循环每经过一轮,剩余数字中的最大值仍然是被移动到当前轮次的最后一位。
在下一轮比较时,只需比较到上一轮比较中,最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换,必然已经有序了。
当一轮比较中从头到尾都没有发生过交换,则表示整个列表已经有序,排序完成。
比如说:从5元素数组,后2位是排好序的,2,3,1,4,5,遍历到元素4,indexOfLastUnsortedElement 被标记,下次遍历到元素1的位置再冒泡就行。
时间复杂度 & 空间复杂度分析
冒泡排序从 1956 年就有人开始研究,之后经历过多次优化。它的空间复杂度为 O(1),时间复杂度为 O(n^2),第二种、第三种冒泡排序由于经过优化,最好的情况下只需要 O(n) 的时间复杂度。
最好情况:在数组已经有序的情况下,只需遍历一次,由于没有发生交换,排序结束。
最差情况:数组顺序为逆序,每次比较都会发生交换。
但优化后的冒泡排序平均时间复杂度仍然是 O(n^2),所以这些优化对算法的性能并没有质的提升。正如 Donald E. Knuth(19741974 年图灵奖获得者)所言:“冒泡排序法除了它迷人的名字和导致了某些有趣的理论问题这一事实外,似乎没有什么值得推荐的。”
小技巧
两数交换技巧
一般来说,交换数组中两个数字的函数如下:
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
但在大厂面试中,有一道非常经典的数字交换题目:如何在不引入第三个中间变量的情况下,完成两个数字的交换。
这里可以用到一个数学上的技巧:
arr[j + 1] = arr[j + 1] + arr[j];
arr[j] = arr[j + 1] - arr[j];
arr[j + 1] = arr[j + 1] - arr[j];
除了这种先加后减的写法,还有一种先减后加的写法:
arr[j + 1] = arr[j] - arr[j + 1];
arr[j] = arr[j] - arr[j + 1];
arr[j + 1] = arr[j + 1] + arr[j];
但这两种方式都可能导致数字越界。
更好的方案是通过位运算完成数字交换:
如下面代码:
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[j] ^ arr[i];
arr[i] = arr[i] ^ arr[j];
以上是关于冒泡排序算法有几种写法?的主要内容,如果未能解决你的问题,请参考以下文章