xgboost导读及论文理解
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了xgboost导读及论文理解相关的知识,希望对你有一定的参考价值。
参考技术A 优化的分布式梯度提升算法,end-to-end 不需要特征抽取。输入原始数据,就能输出目标结果。整篇论文技术实现分两个部分
显而易见,xgboost是非线性(Tree)的加法模型
如果是回归问题则可能是:
而分类问题则应该是交叉熵, 此处 :
二分类问题:
多分类问题:
这里review一下,对于多分类及二分类,交叉熵及soft公式,二分类均是多分类的特例
:
:
原文描述:Default direction, 按我的理解应该是:每轮迭代,每颗树对待一个特征缺失的方向处理应该是一致的,但是不同特征的缺失方向是随机的;不同的迭代子树,策略也是随机的
在建树的过程中,最耗时是找最优的切分点,而这个过程中,最耗时的部分是 将数据排序 。为了减少排序的时间,Xgboost采用 Block结构 存储数据(Data in each block is stored in the compressed column (CSC) format, with each column sorted by the corresponding feature value)
对于approximate算法来说,Xgboost使用了多个Block,存在多个机器上或者磁盘中。每个Block对应原来数据的子集。不同的Block可以在不同的机器上计算。该方法对Local策略尤其有效,因为Local策略每次分支都重新生成候选切分点。
使用Block结构的一个缺点是取梯度的时候,是通过索引来获取的,而这些梯度的获取顺序是按照特征的大小顺序的。这将导致非连续的内存访问,可能使得CPU cache缓存命中率低,从而影响算法效率
在非近似的贪心算法中, 使用 缓存预取(cache-aware prefetching) 。具体来说,对每个线程分配一个连续的buffer,读取梯度信息并存入Buffer中(这样就实现了非连续到连续的转化),然后再统计梯度信息
在近似 算法中,对Block的大小进行了合理的设置。 定义Block的大小为Block中最多的样本数 。设置合适的大小是很重要的,设置过大则容易导致命中率低,过小则容易导致并行化效率不高。经过实验,发现2^16比较好
当数据量太大不能全部放入主内存的时候,为了使得out-of-core计算称为可能,将数据划分为多个Block并存放在磁盘上。计算的时候,使用独立的线程预先将Block放入主内存,因此可以在计算的同时读取磁盘。但是由于磁盘IO速度太慢,通常更不上计算的速度。因此,需要提升磁盘IO的销量。Xgboost采用了2个策略:
Block压缩(Block Compression):将Block按列压缩(LZ4压缩算法?),读取的时候用另外的线程解压。对于行索引,只保存第一个索引值,然后只保存该数据与第一个索引值之差(offset),一共用16个bits来保存
offset,因此,一个block一般有2的16次方个样本。
Block拆分(Block Sharding):将数据划分到不同磁盘上,为每个磁盘分配一个预取(pre-fetcher)线程,并将数据提取到内存缓冲区中。然后,训练线程交替地从每个缓冲区读取数据。这有助于在多个磁盘可用时增加磁盘读取的吞吐量。
[1] R. Bekkerman. The present and the future of the kdd cup competition: an outsider’s perspective. (xgboost应用)
[2] R. Bekkerman, M. Bilenko, and J. Langford. Scaling Up Machine Learning: Parallel and Distributed Approaches. Cambridge University Press, New York, NY, USA, 2011.(并行分布式设计)
[3] J. Bennett and S. Lanning. The netflix prize. In Proceedings of the KDD Cup Workshop 2007, pages 3–6, New York, Aug. 2007.(xgboost应用)
[4] L. Breiman. Random forests. Maching Learning, 45(1):5–32, Oct. 2001.(Breiman随机森林论文)
[5] C. Burges. From ranknet to lambdarank to lambdamart: An overview. Learning, 11:23–581, 2010.
[6] O. Chapelle and Y. Chang. Yahoo! Learning to Rank Challenge Overview. Journal of Machine Learning Research - W & CP, 14:1–24, 2011.(xgboost应用)
[7] T. Chen, H. Li, Q. Yang, and Y. Yu. General functional matrix factorization using gradient boosting. In Proceeding
of 30th International Conference on Machine Learning(通过梯度提升的方法来实现general的矩阵分解)
(ICML’13), volume 1, pages 436–444, 2013.
[8] T. Chen, S. Singh, B. Taskar, and C. Guestrin. Efficient
second-order gradient boosting for conditional random fields. In Proceeding of 18th Artificial Intelligence and Statistics Conference (AISTATS’15), volume 1, 2015.(二阶导boost实现的条件随机场)
[9] R.-E. Fan, K.-W. Chang, C.-J. Hsieh, X.-R. Wang, and C.-J. Lin. LIBLINEAR: A library for large linear classification. Journal of Machine Learning Research, 9:1871–1874, 2008.(xgboost应用)
[10] J. Friedman. Greedy function approximation: a gradient boosting machine. Annals of Statistics, 29(5):1189–1232, 2001.(gbm的贪心算法实现)
[11] J. Friedman. Stochastic gradient boosting. Computational Statistics & Data Analysis, 38(4):367–378, 2002.
(随机梯度下降)
[12] J. Friedman, T. Hastie, and R. Tibshirani. Additive logistic regression: a statistical view of boosting. Annals of Statistics, 28(2):337–407, 2000.(叠加式的逻辑回归方式)
[13] J. H. Friedman and B. E. Popescu. Importance sampled learning ensembles, 2003.(采样学习)
[14] M. Greenwald and S. Khanna. Space-efficient online computation of quantile summaries. In Proceedings of the 2001 ACM SIGMOD International Conference on Management of Data, pages 58–66, 2001.
[15] X. He, J. Pan, O. Jin, T. Xu, B. Liu, T. Xu, Y. Shi,
A. Atallah, R. Herbrich, S. Bowers, and J. Q. n. Candela. Practical lessons from predicting clicks on ads at facebook. In
Proceedings of the Eighth International Workshop on Data Mining for Online Advertising, ADKDD’14, 2014.(xgboost应用)
[16] P. Li. Robust Logitboost and adaptive base class (ABC) Logitboost. In Proceedings of the Twenty-Sixth Conference Annual Conference on Uncertainty in Artificial Intelligence (UAI’10), pages 302–311, 2010.(logitboost)
[17] P. Li, Q. Wu, and C. J. Burges. Mcrank: Learning to rank using multiple classification and gradient boosting. In Advances in Neural Information Processing Systems 20, pages 897–904. 2008.(多分类应用)
[18] X. Meng, J. Bradley, B. Yavuz, E. Sparks,
S. Venkataraman, D. Liu, J. Freeman, D. Tsai, M. Amde, S. Owen, D. Xin, R. Xin, M. J. Franklin, R. Zadeh,
M. Zaharia, and A. Talwalkar. MLlib: Machine learning in apache spark.
Journal of Machine Learning Research, 17(34):1–7, 2016.(分布式机器学习设计)
[19] B. Panda, J. S. Herbach, S. Basu, and R. J. Bayardo. Planet: Massively parallel learning of tree ensembles with mapreduce. Proceeding of VLDB Endowment, 2(2):1426–1437, Aug. 2009.(分布式机器学习设计)
[20] F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel,
B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer,
R. Weiss, V. Dubourg, J. Vanderplas, A. Passos,
D. Cournapeau, M. Brucher, M. Perrot, and E. Duchesnay. Scikit-learn: Machine learning in Python.
Journal of Machine Learning Research, 12:2825–2830, 2011.(sklearn)
[21] G. Ridgeway. Generalized Boosted Models: A guide to the gbm package.
[22] S. Tyree, K. Weinberger, K. Agrawal, and J. Paykin. Parallel boosted regression trees for web search ranking. In Proceedings of the 20th international conference on World wide web, pages 387–396. ACM, 2011.
[23] J. Ye, J.-H. Chow, J. Chen, and Z. Zheng. Stochastic gradient boosted distributed decision trees. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, CIKM ’09.
[24] Q. Zhang and W. Wang. A fast algorithm for approximate quantiles in high speed data streams. In Proceedings of the 19th International Conference on Scientific and Statistical Database Management, 2007.(数据处理加速计算)
[25] T. Zhang and R. Johnson. Learning nonlinear functions using regularized greedy forest. IEEE Transactions on Pattern Analysis and Machine Intelligence, 36(5), 2014.
深入理解XGBoost,优缺点分析,原理推导及工程实现
本文的主要内容概览:
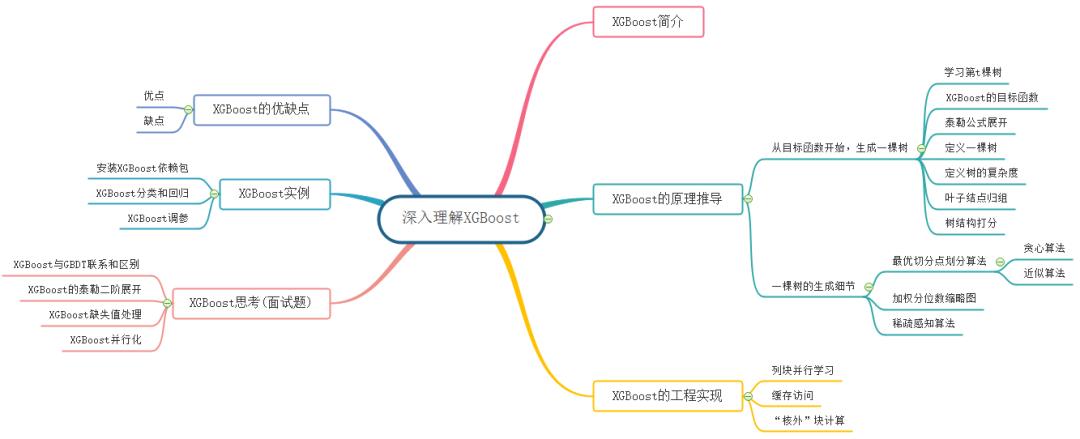
1. XGBoost简介
XGBoost的全称是eXtreme Gradient Boosting,它是经过优化的分布式梯度提升库,旨在高效、灵活且可移植。XGBoost是大规模并行boosting tree的工具,它是目前最快最好的开源 boosting tree工具包,比常见的工具包快10倍以上。在数据科学方面,有大量的Kaggle选手选用XGBoost进行数据挖掘比赛,是各大数据科学比赛的必杀武器;在工业界大规模数据方面,XGBoost的分布式版本有广泛的可移植性,支持在Kubernetes、Hadoop、SGE、MPI、 Dask等各个分布式环境上运行,使得它可以很好地解决工业界大规模数据的问题。本文将从XGBoost的数学原理和工程实现上进行介绍,然后介绍XGBoost的优缺点,并在最后给出面试中经常遇到的关于XGBoost的问题。
2. XGBoost的原理推导
2.1 从目标函数开始,生成一棵树
XGBoost和GBDT两者都是boosting方法,除了工程实现、解决问题上的一些差异外,最大的不同就是目标函数的定义。因此,本文我们从目标函数开始探究XGBoost的基本原理。
2.1.1 学习第 t 棵树
XGBoost是由 个基模型组成的一个加法模型,假设我们第 次迭代要训练的树模型是 ,则有:

2.1.2 XGBoost的目标函数
损失函数可由预测值 与真实值 进行表示:
其中, 为样本的数量。
我们知道模型的预测精度由模型的偏差和方差共同决定,损失函数代表了模型的偏差,想要方差小则需要在目标函数中添加正则项,用于防止过拟合。所以目标函数由模型的损失函数 与抑制模型复杂度的正则项 组成,目标函数的定义如下:
其中, 是将全部 棵树的复杂度进行求和,添加到目标函数中作为正则化项,用于防止模型过度拟合。
由于XGBoost是boosting族中的算法,所以遵从前向分步加法,以第 步的模型为例,模型对第 个样本 的预测值为:
其中, 是由第 步的模型给出的预测值,是已知常数, 是这次需要加入的新模型的预测值。此时,目标函数就可以写成:
注意上式中,只有一个变量,那就是第 棵树 ,其余都是已知量或可通过已知量可以计算出来的。细心的同学可能会问,上式中的第二行到第三行是如何得到的呢?这里我们将正则化项进行拆分,由于前 棵树的结构已经确定,因此前 棵树的复杂度之和可以用一个常量表示,如下所示:
2.1.3 泰勒公式展开
泰勒公式是将一个在 处具有 阶导数的函数 利用关于 的 次多项式来逼近函数的方法。若函数 在包含 的某个闭区间 上具有 阶导数,且在开区间