什么是启发式搜索?并以八数码难题为例,说明其原理

Posted 2023-04-23

参考技术A 启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。我们先看看估价是如何表示的。
　　启发中的估价是用估价函数表示的，如：
　　最佳优先搜索的最广为人知的形式称为A*搜索(发音为“A星搜索”).它把到达节点的耗散g(n)
　　和从该节点到目标节点的消耗h(n)结合起来对节点进行评价：f(n)=g(n)+h(n)
　　因为以g(n)给出了从起始节点到节点n的路径耗散，而h(n)是从节点n到目标节点的最低耗散路径的估计耗散值，因此f(n)=经过节点n的最低耗散解的估计耗散.这样，如果我们想要找到最低耗散解，首先尝试找到g(n)+h(n)值最小的节点是合理的。可以发现这个策略不只是合理的:倘若启发函数h(n)满足一定的条件，A*搜索既是完备的也是最优的。
　　如果把A*搜索用于Tree-Search,它的最优性是能够直接分折的。在这种情况下，如果h(n)是一个可采纳启发式--也就是说，倘若h(n)从不会过高估计到达目标的耗散--A*算法是最优的。可采纳启发式天生是最优的，因为他们认为求解问题的耗散是低于实际耗散的。因为g(n)是到达节点n的确切耗散，我们得到一个直接的结论：f(n)永远不会高估经过节点n的解的实际耗散.
　　启发算法有：
蚁群算法，遗传算法、模拟退火算法等
　　蚁群算法是一种来自大自然的随机搜索寻优方法，是生物界的群体启发式行为，现己陆续应用到组合优化、人工智能、通讯等多个领域。蚁群算法的正反馈性和协同性使其可用于分布式系统，隐含的并行性更使之具有极强的发展潜力。从数值仿真结果来看，它比目前风行一时的遗传算法、模拟退火算法等有更好的适应性。

A*算法求解N数码

A*算法实验

实验目的：

1.熟悉启发式搜索的定义、估价函数和算法过程
2.利用A*算法求解N数码难题，理解求解流程和搜索顺序
3.熟练掌握numpy库的相关函数（单独库，需要使用‘pip install numpy’安装）

实验原理：

A*算法是一种启发式图搜索算法，其特点在于对估价函数的定义上。对于一般的启发式图搜索，总是选择估价函数f值最小的节点作为扩展节点。因此，f是根据需要找到一条最小代价路径的观点来估算节点的，所以，可考虑每个节点n的估价函数值为两个分量：从起始节点到节点n的实际代价以及从节点n到达目标节点的估价代价。

实验内容：

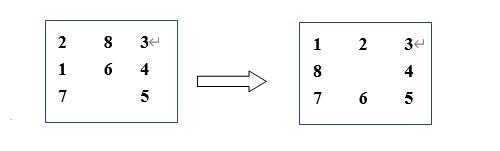
1 、以8数码问题为例实现A*算法的求解程序。

估价函数f(n) = g(n) + h(n)
g(n)=d(n)——结点n在搜索树中的深度
h(n)可选择h1(n)——结点n中“不在位”的数码个数 或 h2(n) =p(n)= 将牌“不在位”的距离和

代码实现：

import numpy as np
def change (str):#提取输入到数字，合成数组
    list=[]
    for i in range(0,len(str)):
        list.append(str[i])
    a = np.array(list)
    b = a.reshape(hang,lie)
    return b
def h(newnumber,endnumber):#计算两个数码间位置不同的数字的个数
    h=0
    for i in range(0,hang):
        for j in range(0,lie):
            if (newnumber[i][j]!=endnumber[i][j]):
                h+=1
            else:
                continue
    return h
def g(newnumber,endnumber):#计算每个数字最近的路径之和
    g=0
    for i in range(0,hang):
        for j in range(0,lie):
            if (newnumber[i][j]!=endnumber[i][j]):
                g+=((abs((i-end[newnumber[i][j]][0])))+(abs((j-end[newnumber[i][j]][1]))))
            else:
                continue
    return g
def kongid(newnumber):#判断空格的位置
    for i in range(0,hang):
        for j in range(0,lie):
            if (newnumber[i][j]==' '):
                id=(i,j)
                return id
def same(newnumber,endnumber):#比较两个数组是否相等，相等返回True，不相等返回False
    a=(newnumber==endnumber)
    e=a.all()
    if(e):
        return True
    else:
        return False
def A(newnumber,endnumber):#变化N字码
   if (same(newnumber,endnumber)):
       return True
   else:
       xx=hang*lie*10
       l1n=xx
       l2n=xx
       l3n=xx
       l4n=xx
       a=kongid(newnumber)
       l1=newnumber.copy()
       l2=newnumber.copy()
       l3=newnumber.copy()
       l4=newnumber.copy()
       l0=newnumber[a[0]][a[1]]
       if((a[0]-1)>=0):
           l1[a[0]][a[1]]=newnumber[a[0]-1][a[1]]
           l1[a[0]-1][a[1]]=l0
           l1h=h(l1,endnumber)
           l1g=g(l1,endnumber)
           l1n=l1g+l1h
       if((a[0]+1)<=(hang-1)):
           l2[a[0]][a[1]]=newnumber[a[0]+1][a[1]]
           l2[a[0]+1][a[1]]=l0
           l2h=h(l2,endnumber)
           l2g=g(l2,endnumber)
           l2n=l2g+l2h
       if((a[1]-1)>=0):
           l3[a[0]][a[1]]=newnumber[a[0]][a[1]-1]
           l3[a[0]][a[1]-1]=l0
           l3h=h(l3,endnumber)
           l3g=g(l3,endnumber)
           l3n=l3g+l3h
       if((a[1]+1)<=(lie-1)):
           l4[a[0]][a[1]]=newnumber[a[0]][a[1]+1]
           l4[a[0]][a[1]+1]=l0
           l4h=h(l4,endnumber)
           l4g=g(l4,endnumber)
           l4n=l4g+l4h
       return [l1,l2,l3,l4,l1n,l2n,l3n,l4n]
while (True):
    str=input("输入要变化的数码问题的顺序（数据自左到右，自上到下）：")
    str1=input("输入变化后的数码问题的顺序（数据自左到右，自上到下）：")
    heng=input("输入数码的行数：")
    shu=input("输入数码的列数：")
    hang=int(heng)
    lie=int(shu)
    if ((hang*lie)==len(str) and ((hang*lie)==len(str1))):
        break
    else:
        if (hang*lie)==len(str):
            print("要变化的数码问题错误，返回至输入项——>>>")
        elif ((hang*lie)==len(str1)):
            print("输入的变化后的数码错误，返回至输入项——>>>")
        else:
            print("数码的格式错误，返回至输入项——>>>")
#print(str[0])
newnumber = change(str)
endnumber = change(str1)
end = dict()
for i in range(0,hang):
    for j in range(0,lie):
        end[endnumber[i][j]]=(i,j)
m=h(newnumber,endnumber)
n=g(newnumber,endnumber)
open=[]
maind = A(newnumber, endnumber)
while(True):

    if(maind==True):
        break
    else:
        for i in range(0,len(open)):
            if (same(maind[0],open[i])):
                maind[4]=hang*lie*10
            if(same(maind[1],open[i])):
                maind[5]=hang*lie*10
            if(same(maind[2],open[i])):
                maind[6]=hang*lie*10
            if(same(maind[3],open[i])):
                maind[7]=hang*lie*10
    l1=maind[0]
    l2=maind[1]
    l3=maind[2]
    l4=maind[3]
    l1n=maind[4]
    l2n=maind[5]
    l3n=maind[6]
    l4n=maind[7]
    if (l1n <= l2n):
        if (l3n <= l4n):
            if (l1n <= l3n):
                print(l1)
                maind = A(l1, endnumber)
                open.append(l1)
                continue
            else:
                print(l3)
                maind = A(l3, endnumber)
                open.append(l3)
                continue
        else:
            if (l1n <= l4n):
                print(l1)
                maind = A(l1, endnumber)
                open.append(l1)
                continue
            else:
                print(l4)
                maind = A(l4, endnumber)
                open.append(l4)
                continue
    else:
        if (l3n <= l4n):
            if (l2n <= l3n):
                print(l2)
                maind = A(l2, endnumber)
                open.append(l2)
                continue
            else:
                print(l3)
                maind = A(l3, endnumber)
                open.append(l3)
                continue
        else:
            if (l2n <= l4n):
                print(l2)
                maind = A(l2, endnumber)
                open.append(l2)
                continue
            else:
                print(l4)
                maind = A(l4, endnumber)
                open.append(l4)
                continue

实验结果：

以上方例子运行代码，结果如下：

输入要变化的数码问题的顺序（数据自左到右，自上到下）：2831647 5
输入变化后的数码问题的顺序（数据自左到右，自上到下）：1238 4765
输入数码的行数：3
输入数码的列数：3
[['2' '8' '3']
 ['1' ' ' '4']
 ['7' '6' '5']]
[['2' ' ' '3']
 ['1' '8' '4']
 ['7' '6' '5']]
[[' ' '2' '3']
 ['1' '8' '4']
 ['7' '6' '5']]
[['1' '2' '3']
 [' ' '8' '4']
 ['7' '6' '5']]
[['1' '2' '3']
 ['8' ' ' '4']
 ['7' '6' '5']]