如何用Python实现支持向量机
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何用Python实现支持向量机相关的知识,希望对你有一定的参考价值。
看这个文章blog.csdn.net/zouxy09/article/details/17292011
机器学习算法与Python实践之(四)支持向量机(SVM)实现 参考技术A 终于到SVM的实现部分了。那么神奇和有效的东西还得回归到实现才可以展示其强大的功力。SVM有效而且存在很高效的训练算法,这也是工业界非常青睐SVM的原因。
前面讲到,SVM的学习问题可以转化为下面的对偶问题:
需要满足的KKT条件:
也就是说找到一组αi可以满足上面的这些条件的就是该目标的一个最优解。所以我们的优化目标是找到一组最优的αi*。一旦求出这些αi*,就很容易计算出权重向量w*和b,并得到分隔超平面了。
这是个凸二次规划问题,它具有全局最优解,一般可以通过现有的工具来优化。但当训练样本非常多的时候,这些优化算法往往非常耗时低效,以致无法使用。从SVM提出到现在,也出现了很多优化训练的方法。其中,非常出名的一个是1982年由Microsoft Research的John C. Platt在论文《Sequential Minimal Optimization: A Fast Algorithm for TrainingSupport Vector Machines》中提出的Sequential Minimal Optimization序列最小化优化算法,简称SMO算法。SMO算法的思想很简单,它将大优化的问题分解成多个小优化的问题。这些小问题往往比较容易求解,并且对他们进行顺序求解的结果与将他们作为整体来求解的结果完全一致。在结果完全一致的同时,SMO的求解时间短很多。在深入SMO算法之前,我们先来了解下坐标下降这个算法,SMO其实基于这种简单的思想的。
8.1、坐标下降(上升)法
假设要求解下面的优化问题:
在这里,我们需要求解m个变量αi,一般来说是通过梯度下降(这里是求最大值,所以应该叫上升)等算法每一次迭代对所有m个变量αi也就是α向量进行一次性优化。通过误差每次迭代调整α向量中每个元素的值。而坐标上升法(坐标上升与坐标下降可以看做是一对,坐标上升是用来求解max最优化问题,坐标下降用于求min最优化问题)的思想是每次迭代只调整一个变量αi的值,其他变量的值在这次迭代中固定不变。
最里面语句的意思是固定除αi之外的所有αj(i不等于j),这时W可看作只是关于αi的函数,那么直接对αi求导优化即可。这里我们进行最大化求导的顺序i是从1到m,可以通过更改优化顺序来使W能够更快地增加并收敛。如果W在内循环中能够很快地达到最优,那么坐标上升法会是一个很高效的求极值方法。
用个二维的例子来说明下坐标下降法:我们需要寻找f(x,y)=x2+xy+y2的最小值处的(x*, y*),也就是下图的F*点的地方。
假设我们初始的点是A(图是函数投影到xoy平面的等高线图,颜色越深值越小),我们需要达到F*的地方。那最快的方法就是图中黄色线的路径,一次性就到达了,其实这个是牛顿优化法,但如果是高维的话,这个方法就不太高效了(因为需要求解矩阵的逆,这个不在这里讨论)。我们也可以按照红色所指示的路径来走。从A开始,先固定x,沿着y轴往让f(x, y)值减小的方向走到B点,然后固定y,沿着x轴往让f(x, y)值减小的方向走到C点,不断循环,直到到达F*。反正每次只要我们都往让f(x, y)值小的地方走就行了,这样脚踏实地,一步步走,每一步都使f(x, y)慢慢变小,总有一天,皇天不负有心人的。到达F*也是时间问题。到这里你可能会说,这红色线比黄色线贫富差距也太严重了吧。因为这里是二维的简单的情况嘛。如果是高维的情况,而且目标函数很复杂的话,再加上样本集很多,那么在梯度下降中,目标函数对所有αi求梯度或者在牛顿法中对矩阵求逆,都是很耗时的。这时候,如果W只对单个αi优化很快的时候,坐标下降法可能会更加高效。
8.2、SMO算法
SMO算法的思想和坐标下降法的思想差不多。唯一不同的是,SMO是一次迭代优化两个α而不是一个。为什么要优化两个呢?
我们回到这个优化问题。我们可以看到这个优化问题存在着一个约束,也就是
假设我们首先固定除α1以外的所有参数,然后在α1上求极值。但需要注意的是,因为如果固定α1以外的所有参数,由上面这个约束条件可以知道,α1将不再是变量(可以由其他值推出),因为问题中规定了:
因此,我们需要一次选取两个参数做优化,比如αi和αj,此时αi可以由αj和其他参数表示出来。这样回代入W中,W就只是关于αj的函数了,这时候就可以只对αj进行优化了。在这里就是对αj进行求导,令导数为0就可以解出这个时候最优的αj了。然后也可以得到αi。这就是一次的迭代过程,一次迭代只调整两个拉格朗日乘子αi和αj。SMO之所以高效就是因为在固定其他参数后,对一个参数优化过程很高效(对一个参数的优化可以通过解析求解,而不是迭代。虽然对一个参数的一次最小优化不可能保证其结果就是所优化的拉格朗日乘子的最终结果,但会使目标函数向极小值迈进一步,这样对所有的乘子做最小优化,直到所有满足KKT条件时,目标函数达到最小)。
总结下来是:
重复下面过程直到收敛
(1)选择两个拉格朗日乘子αi和αj;
(2)固定其他拉格朗日乘子αk(k不等于i和j),只对αi和αj优化w(α);
(3)根据优化后的αi和αj,更新截距b的值;
参考技术B 支持封装API都JAVA写
机器学习之支持向量机:支持向量机的Python语言实现
注:关于支持向量机系列文章是借鉴大神的神作,加以自己的理解写成的;若对原作者有损请告知,我会及时处理。转载请标明来源。
序:
我在支持向量机系列中主要讲支持向量机的公式推导,第一部分讲到推出拉格朗日对偶函数的对偶因子α;第二部分是SMO算法对于对偶因子的求解;第三部分是核函数的原理与应用,讲核函数的推理及常用的核函数有哪些;第四部分是支持向量机的应用,按照机器学习实战的代码详细解读。
机器学习之支持向量机(四):支持向量机的Python语言实现
1 数据样本集的介绍
这篇文章是根据《机器学习实战》一书的实例进行代码的详细解读,我在查找这方面的资料没有人对支持向量机算法 python 实现的详细说明,我就把我在看代码时的思路和代码详细注解。如果存在不足,欢迎给我留言相互探讨。好了,废话不多说,正文开始。。。
首先我们使用的数据是二维的坐标点,还有对应的类标号(1 或 -1)。数据集以 “testSet.txt” 命名,如下代码段中:

1 3.542485 1.977398 -1 2 3.018896 2.556416 -1 3 7.551510 -1.580030 1 4 2.114999 -0.004466 -1 5 8.127113 1.274372 1 6 7.108772 -0.986906 1 7 8.610639 2.046708 1 8 2.326297 0.265213 -1 9 3.634009 1.730537 -1 10 0.341367 -0.894998 -1 11 3.125951 0.293251 -1 12 2.123252 -0.783563 -1 13 0.887835 -2.797792 -1 14 7.139979 -2.329896 1 15 1.696414 -1.212496 -1 16 8.117032 0.623493 1 17 8.497162 -0.266649 1 18 4.658191 3.507396 -1 19 8.197181 1.545132 1 20 1.208047 0.213100 -1 21 1.928486 -0.321870 -1 22 2.175808 -0.014527 -1 23 7.886608 0.461755 1 24 3.223038 -0.552392 -1 25 3.628502 2.190585 -1 26 7.407860 -0.121961 1 27 7.286357 0.251077 1 28 2.301095 -0.533988 -1 29 -0.232542 -0.547690 -1 30 3.457096 -0.082216 -1 31 3.023938 -0.057392 -1 32 8.015003 0.885325 1 33 8.991748 0.923154 1 34 7.916831 -1.781735 1 35 7.616862 -0.217958 1 36 2.450939 0.744967 -1 37 7.270337 -2.507834 1 38 1.749721 -0.961902 -1 39 1.803111 -0.176349 -1 40 8.804461 3.044301 1 41 1.231257 -0.568573 -1 42 2.074915 1.410550 -1 43 -0.743036 -1.736103 -1 44 3.536555 3.964960 -1 45 8.410143 0.025606 1 46 7.382988 -0.478764 1 47 6.960661 -0.245353 1 48 8.234460 0.701868 1 49 8.168618 -0.903835 1 50 1.534187 -0.622492 -1 51 9.229518 2.066088 1 52 7.886242 0.191813 1 53 2.893743 -1.643468 -1 54 1.870457 -1.040420 -1 55 5.286862 -2.358286 1 56 6.080573 0.418886 1 57 2.544314 1.714165 -1 58 6.016004 -3.753712 1 59 0.926310 -0.564359 -1 60 0.870296 -0.109952 -1 61 2.369345 1.375695 -1 62 1.363782 -0.254082 -1 63 7.279460 -0.189572 1 64 1.896005 0.515080 -1 65 8.102154 -0.603875 1 66 2.529893 0.662657 -1 67 1.963874 -0.365233 -1 68 8.132048 0.785914 1 69 8.245938 0.372366 1 70 6.543888 0.433164 1 71 -0.236713 -5.766721 -1 72 8.112593 0.295839 1 73 9.803425 1.495167 1 74 1.497407 -0.552916 -1 75 1.336267 -1.632889 -1 76 9.205805 -0.586480 1 77 1.966279 -1.840439 -1 78 8.398012 1.584918 1 79 7.239953 -1.764292 1 80 7.556201 0.241185 1 81 9.015509 0.345019 1 82 8.266085 -0.230977 1 83 8.545620 2.788799 1 84 9.295969 1.346332 1 85 2.404234 0.570278 -1 86 2.037772 0.021919 -1 87 1.727631 -0.453143 -1 88 1.979395 -0.050773 -1 89 8.092288 -1.372433 1 90 1.667645 0.239204 -1 91 9.854303 1.365116 1 92 7.921057 -1.327587 1 93 8.500757 1.492372 1 94 1.339746 -0.291183 -1 95 3.107511 0.758367 -1 96 2.609525 0.902979 -1 97 3.263585 1.367898 -1 98 2.912122 -0.202359 -1 99 1.731786 0.589096 -1 100 2.387003 1.573131 -1
然后,数据集中对象在下图显示,我们的工作就是找到最佳的超平面(这里是直线)。
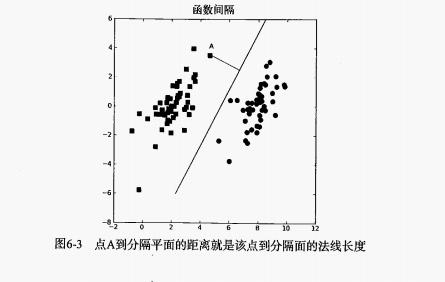
2 Python 代码的实现
2.1 准备数据和分析数据
既然我们有了数据,那么就要把数据转换成可以被程序调用和处理的形式。写一个加载数据的函数,把文本中的数据转化成列表类型。代码如下:
1 # 将文本中的样本数据添加到列表中 2 def loadDataSet(fileName): 3 dataMat = [] 4 labelMat = [] 5 fr = open(fileName) 6 for line in fr.readlines() : # 对文本按行遍历 7 lineArr = line.strip().split(\'\\t\') 8 dataMat .append([float(lineArr [0]), float(lineArr[1])]) # 每行前两个是属性数据,最后一个是类标号 9 labelMat .append(float(lineArr[2])) 10 return dataMat , labelMat
由于在实现支持向量机的过程中要多次调用样本数据、类标号、对偶因子、对象经过核函数映射之后的值和其他数据,因此利用创造一个类,初始化这些数据利于保存和调用。代码如下:
1 class optStruct: 2 def __init__(self,dataMatIn, classLabels, C, toler, kTup): 3 self.X = dataMatIn # 样本数据 4 self.labelMat = classLabels # 样本的类标号 5 self.C = C # 对偶因子的上界值 6 self.tol = toler 7 self.m = shape(dataMatIn)[0] # 样本的行数,即样本对象的个数 8 self.alphas = mat(zeros((self.m, 1))) # 对偶因子 9 self.b = 0 # 分割函数的截距 10 self.eCache = mat(zeros((self.m, 2))) # 差值矩阵 m * 2,第一列是对象的标志位 1 表示存在不为零的差值 0 表示差值为零,第二列是实际的差值 E 11 self.K = mat(zeros((self.m, self.m))) # 对象经过核函数映射之后的值 12 for i in range(self.m): # 遍历全部样本集 13 self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup ) # 调用径向基核函数
2.2 对偶因子的求解函数
我们通过支持向量机(二):SMO算法,可知对偶因子是我们求得超平面的关键,只有解得对偶因子才能得到超平面的法向量和截距。代码如下:
1 # 遍历所有能优化的 alpha 2 def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=(\'lin\', 0)): 3 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup) # 创建一个类对象 oS ,类对象 oS 存放所有数据 4 iter = 0 # 迭代次数的初始化 5 entireSet = True # 违反 KKT 条件的标志符 6 alphaPairsChanged = 0 # 迭代中优化的次数 7 8 # 从选择第一个 alpha 开始,优化所有alpha 9 while(iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet )): # 优化的终止条件:在规定迭代次数下,是否遍历了整个样本或 alpha 是否优化 10 alphaPairsChanged = 0 11 if entireSet: # 12 for i in range(oS.m): # 遍历所有对象 13 alphaPairsChanged += innerL(i ,oS) # 调用优化函数(不一定优化) 14 print "fullSet , iter: %d i %d, pairs changed %d" % (iter, i , alphaPairsChanged ) 15 iter += 1 # 迭代次数加 1 16 else: 17 nonBoundIs = nonzero((oS.alphas .A > 0) * (oS.alphas.A < C))[0] 18 for i in nonBoundIs : # 遍历所有非边界样本集 19 alphaPairsChanged += innerL(i, oS) # 调用优化函数(不一定优化) 20 print "non-bound, iter: %d i :%d, pairs changed %d" % (iter, i, alphaPairsChanged ) 21 iter += 1 # 迭代次数加 1 22 if entireSet : # 没有违反KKT 条件的alpha ,终止迭代 23 entireSet = False 24 elif (alphaPairsChanged == 0): # 存在违反 KKT 的alpha 25 entireSet = True 26 print "iteration number: %d" % iter 27 return oS.b, oS.alphas # 返回截距值和 alphas
上述代码中,第 13 行调用了 innerL() 函数,它是对对偶因子向量的单个元素求解。代码如下:
1 # 优化选取两个 alpha ,并计算截距 b 2 def innerL(i, oS): 3 Ei = calcEk(oS, i) # 计算 对象 i 的差值 4 # 第一个 alpha 符合选择条件进入优化 5 if ((oS.labelMat [i]*Ei <- oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat [i]*Ei > oS.tol) and (oS.alphas[i] > 0)): 6 j,Ej =selectJ(i, oS, Ei) # 选择第二个 alpha 7 alphaIold = oS.alphas[i].copy() # 浅拷贝 8 alphaJold = oS.alphas[j].copy() # 浅拷贝 9 10 # 根据对象 i 、j 的类标号(相等或不等)确定KKT条件的上界和下界 11 if (oS.labelMat[i] != oS.labelMat[j]): 12 L = max(0, oS.alphas [j] - oS.alphas[i]) 13 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 14 else : 15 L = max(0, oS.alphas[j] + oS.alphas [i] - oS.C) 16 H = min(oS.C, oS.alphas [j] + oS.alphas [i]) 17 18 if L==H:print "L==H";return 0 # 不符合优化条件(第二个 alpha) 19 eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] # 计算公式的eta ,是公式的相反数 20 if eta >= 0:print "eta>=0";return 0 # 不考虑eta 大于等于 0 的情况(这种情况对 alpha 的解是另外一种方式,即临界情况的求解) 21 # 优化之后的第二个 alpha 值 22 oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 23 oS.alphas[j] = clipAlpha(oS.alphas[j], H, L) 24 updateEk(oS, j) # 更新差值矩阵 25 if (abs(oS.alphas[j] - alphaJold) < 0.00001): # 优化之后的 alpha 值与之前的值改变量太小,步长不足 26 print "j not moving enough" 27 return 0 28 oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j]) # 优化第二个 alpha 29 updateEk(oS, i) # 更新差值矩阵 30 # 计算截距 b 31 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i, j] 32 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j] 33 if (0 < oS.alphas [i]) and (oS.C > oS.alphas[i]): 34 oS.b = b1 35 elif (0 < oS.alphas [j]) and (oS.C > oS.alphas [j]): 36 oS.b = b2 37 else : 38 oS.b = (b1 + b2)/2.0 39 return 1 # 进行一次优化 40 else : 41 return 0
这里第 3 行代码调用了calcEk() 函数,它是计算预测值与真实值的差值。代码如下:
1 # 预测的类标号值与真实值的差值,参数 oS 是类对象,k 是样本的对象的标号 2 def calcEk(oS, k): 3 fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b) # 公式(1) 4 Ek = fXk - float(oS.labelMat[k]) # 差值 5 return Ek
其中,第 3 行中指到的公式(1)是超平面方程。
在 innerL()函数中的第 6 行,调用了 selectJ ()函数,此函数是用来选择优化的第二个对偶因子元素。代码如下:
1 # 由启发式选取第二个 alpha,以最大步长为标准 2 def selectJ(i, oS, Ei): # 函数的参数是选取的第一个 alpha 的对象号、类对象和对象差值 3 maxK = -1; maxDeltaE = 0; Ej = 0 # 第二个 alpha 的初始化 4 oS.eCache[i] = [1,Ei] # 更新差值矩阵的第 i 行 5 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # 取差值矩阵中第一列不为 0 的所有行数(标志位为 1 ),以元组类型返回 6 if (len(validEcacheList)) > 1 : # 7 for k in validEcacheList : # 遍历所有标志位为 1 的对象的差值 8 if k == i: continue 9 Ek = calcEk(oS, k) # 计算对象 k 的差值 10 deltaE = abs(Ei - Ek) # 取两个差值之差的绝对值 11 if (deltaE > maxDeltaE): # 选取最大的绝对值deltaE 12 maxK = k; maxDeltaE = deltaE; Ej = Ek 13 return maxK, Ej # 返回选取的第二个 alpha 14 else: # 随机选取第二个 alpha 15 j = selectJrand(i, oS.m) 16 Ej = calcEk(oS,j) 17 return j, Ej # 返回选取的第二个 alpha
这个函数的第 15 行调用了 selectJrand() 函数,是为了没有合适的第二个元素,就用随机的方式选择。代码如下:
1 # 随机选取对偶因子alpha ,参数i 是alpha 的下标,m 是alpha 的总数 2 def selectJrand(i,m): 3 j = i 4 while (j==i): 5 j = int(random.uniform(0,m)) 6 return j
在innerL()函数中的第 23 行调用 clipAlpha() 函数,是根据KKT 条件对对偶因子的修剪。代码如下:
1 # 对所求的对偶因子按约束条件的修剪 2 def clipAlpha(aj, H, L): # H 为上界,L为下界 3 if aj > H: 4 aj = H 5 if L > aj: 6 aj = L 7 return aj
innerL() 函数的第 29 行调用了 updateEk() 函数,更新差值矩阵的数据。代码如下:
1 # 更新差值矩阵的数据 2 def updateEk(oS, k): 3 Ek = calcEk(oS, k) # 调用计算差值的函数 4 oS.eCache [k] = [1,Ek]
2.3 核函数
这里我们使用的径向基核函数,把数据从低维映射到高维,把不可分数据变成可分。当然,我们给出的数据集是线性可分,现在给出另外数据集,分为训练集“testSetRBF.txt”和测试集"testSetRBF2.txt"。
径向基核函数公式如下:

数据集

1 -0.214824 0.662756 -1.000000 2 -0.061569 -0.091875 1.000000 3 0.406933 0.648055 -1.000000 4 0.223650 0.130142 1.000000 5 0.231317 0.766906 -1.000000 6 -0.748800 -0.531637 -1.000000 7 -0.557789 0.375797 -1.000000 8 0.207123 -0.019463 1.000000 9 0.286462 0.719470 -1.000000 10 0.195300 -0.179039 1.000000 11 -0.152696 -0.153030 1.000000 12 0.384471 0.653336 -1.000000 13 -0.117280 -0.153217 1.000000 14 -0.238076 0.000583 1.000000 15 -0.413576 0.145681 1.000000 16 0.490767 -0.680029 -1.000000 17 0.199894 -0.199381 1.000000 18 -0.356048 0.537960 -1.000000 19 -0.392868 -0.125261 1.000000 20 0.353588 -0.070617 1.000000 21 0.020984 0.925720 -1.000000 22 -0.475167 -0.346247 -1.000000 23 0.074952 0.042783 1.000000 24 0.394164 -0.058217 1.000000 25 0.663418 0.436525 -1.000000 26 0.402158 0.577744 -1.000000 27 -0.449349 -0.038074 1.000000 28 0.619080 -0.088188 -1.000000 29 0.268066 -0.071621 1.000000 30 -0.015165 0.359326 1.000000 31 0.539368 -0.374972 -1.000000 32 -0.319153 0.629673 -1.000000 33 0.694424 0.641180 -1.000000 34 0.079522 0.193198 1.000000 35 0.253289 -0.285861 1.000000 36 -0.035558 -0.010086 1.000000 37 -0.403483 0.474466 -1.000000 38 -0.034312 0.995685 -1.000000 39 -0.590657 0.438051 -1.000000 40 -0.098871 -0.023953 1.000000 41 -0.250001 0.141621 1.000000 42 -0.012998 0.525985 -1.000000 43 0.153738 0.491531 -1.000000 44 0.388215 -0.656567 -1.000000 45 0.049008 0.013499 1.000000 46 0.068286 0.392741 1.000000 47 0.747800 -0.066630 -1.000000 48 0.004621 -0.042932 1.000000 49 -0.701600 0.190983 -1.000000 50 0.055413 -0.024380 1.000000 51 0.035398 -0.333682 1.000000 52 0.211795 0.024689 1.000000 53 -0.045677 0.172907 1.000000 54 0.595222 0.209570 -1.000000 55 0.229465 0.250409 1.000000 56 -0.089293 0.068198 1.000000 57 0.384300 -0.176570 1.000000 58 0.834912 -0.110321 -1.000000 59 -0.307768 0.503038 -1.000000 60 -0.777063 -0.348066 -1.000000 61 0.017390 0.152441 1.000000 62 -0.293382 -0.139778 1.000000 63 -0.203272 0.286855 1.000000 64 0.957812 -0.152444 -1.000000 65 0.004609 -0.070617 1.000000 66 -0.755431 0.096711 -1.000000 67 -0.526487 0.547282 -1.000000 68 -0.246873 0.833713 -1.000000 69 0.185639 -0.066162 1.000000 70 0.851934 0.456603 -1.000000 71 -0.827912 0.117122 -1.000000 72 0.233512 -0.106274 1.000000 73 0.583671 -0.709033 -1.000000 74 -0.487023 0.625140 -1.000000 75 -0.448939 0.176725 1.000000 76 0.155907 -0.166371 1.000000 77 0.334204 0.381237 -1.000000 78 0.081536 -0.106212 1.000000 79 0.227222 0.527437 -1.000000 80 0.759290 0.330720 -1.000000 81 0.204177 -0.023516 1.000000 82 0.577939 0.403784 -1.000000 83 -0.568534 0.442948 -1.000000 84 -0.011520 0.021165 1.000000 85 0.875720 0.422476 -1.000000 86 0.297885 -0.632874 -1.000000 87 -0.015821 0.031226 1.000000 88 0.541359 -0.205969 -1.000000 89 -0.689946 -0.508674 -1.000000 90 -0.343049 0.841653 -1.000000 91 0.523902 -0.436156 -1.000000 92 0.249281 -0.711840 -1.000000 93 0.193449 0.574598 -1.000000 94 -0.257542 -0.753885 -1.000000 95 -0.021605 0.158080 1.000000 96 0.601559 -0.727041 -1.000000 97 -0.791603 0.095651 -1.000000 98 -0.908298 -0.053376 -1.000000 99 0.122020 0.850966 -1.000000 100 -0.725568 -0.292022 -1.000000

1 0.676771 -0.486687 -1.000000 2 0.008473 0.186070 1.000000 3 -0.727789 0.594062 -1.000000 4 0.112367 0.287852 1.000000 5 0.383633 -0.038068 1.000000 6 -0.927138 -0.032633 -1.000000 7 -0.842803 -0.423115 -1.000000 8 -0.003677 -0.367338 1.000000 9 0.443211 -0.698469 -1.000000 10 -0.473835 0.005233 1.000000 11 0.616741 0.590841 -1.000000 12 0.557463 -0.373461 -1.000000 13 -0.498535 -0.223231 -1.000000 14 -0.246744 0.276413 1.000000 15 -0.761980 -0.244188 -1.000000 16 0.641594 -0.479861 -1.000000 17 -0.659140 0.529830 -1.000000 18 -0.054873 -0.238900 1.000000 19 -0.089644 -0.244683 1.000000 20 -0.431576 -0.481538 -1.000000 21 -0.099535 0.728679 -1.000000 22 -0.188428 0.156443 1.000000 23 0.267051 0.318101 1.000000 24 0.222114 -0.528887 -1.000000 25 0.030369 0.113317 1.000000 26 0.392321 0.026089 1.000000 27 0.298871 -0.915427 -1.000000 28 -0.034581 -0.133887 1.000000 29 0.405956 0.206980 1.000000 30 0.144902 -0.605762 -1.000000 31 0.274362 -0.401338 1.000000 32 0.397998 -0.780144 -1.000000 33 0.037863 0.155137 1.000000 34 -0.010363 -0.004170 1.000000 35 0.506519 0.486619 -1.000000 36 0.000082 -0.020625 1.000000 37 0.057761 -0.155140 1.000000 38 0.027748 -0.553763 -1.000000 39 -0.413363 -0.746830 -1.000000 40 0.081500 -0.014264 1.000000 41 0.047137 -0.491271 1.000000 42 -0.267459 0.024770 1.000000 43 -0.148288 -0.532471 -1.000000 44 -0.225559 -0.201622 1.000000 45 0.772360 -0.518986 -1.000000 46 -0.440670 0.688739 -1.000000 47 0.329064 -0.095349 1.000000 48 0.970170 -0.010671 -1.000000 49 -0.689447 -0.318722 -1.000000 50 -0.465493 -0.227468 -1.000000 51 -0.049370 0.405711 1.000000 52 -0.166117 0.274807 1.000000 53 0.054483 0.012643 1.000000 54 0.021389 0.076125 1.000000 55 -0.104404 -0.914042 -1.000000 56 0.294487 0.440886 -1.000000 57 0.107915 -0.493703 -1.000000 58 0.076311 0.438860 1.000000 59 0.370593 -0.728737 -1.000000 60 0.409890 0.306851 -1.000000 61 0.285445 0.474399 -1.000000 62 -0.870134 -0.161685 -1.000000 63 -0.654144 -0.675129 -1.000000 64 0.285278 -0.767310 -1.000000 65 0.049548 -0.000907 1.000000 66 0.030014 -0.093265 1.000000 67 -0.128859 0.278865 1.000000 68 0.307463 0.085667 1.000000 69 0.023440 0.298638 1.000000 70 0.053920 0.235344 1.000000 71 0.059675 0.533339 -1.000000 72 0.817125 0.016536 -1.000000 73 -0.108771 0.477254 1.000000 74 -0.118106 0.017284 1.000000 75 0.288339 0.195457 1.000000 76 0.567309 -0.200203 -1.000000 77 -0.202446 0.409387 1.000000 78 -0.330769 -0.240797 1.000000 79 -0.422377 0.480683 -1.000000 80 -0.295269 0.326017 1.000000 81 0.261132 0.046478 1.000000 82 -0.492244 -0.319998 -1.000000 83 -0.384419 0.099170 1.000000 84 0.101882 -0.781145 -1.000000 85 0.234592 -0.383446 1.000000 86 -0.020478 -0.901833 -1.000000 87 0.328449 0.186633 1.000000 88 -0.150059 -0.409158 1.000000 89 -0.155876 -0.843413 -1.000000 90 -0.098134 -0.136786 1.000000 91 0.110575 -0.197205 1.000000 92 0.219021 0.054347 1.000000 93 0.030152 0.251682 1.000000 94 0.033447 -0.122824 1.000000 95 -0.686225 -0.020779 -1.000000 96 -0.911211 -0.262011 -1.000000 97 0.572557 0.377526 -1.000000 98 -0.073647 -0.519163 -1.000000 99 -0.281830 -0.797236 -1.000000 100 -0.555263 0.126232 -1.000000
核函数代码如下:
1 # 径向基核函数(高斯函数) 2 def kernelTrans(X, A, kTup): # X 是样本集矩阵,A 是样本对象(矩阵的行向量) , kTup 元组 3 m,n = shape(X) 4 K = mat(zeros((m,1))) 5 # 数据不用核函数计算 6 if kTup [0] == \'lin\': K = X * A.T 7 8 # 用径向基核函数计算 9 elif kTup[0] == \'rbf\': 10 for j in range(m): 11 deltaRow = X[j,:] - A 12 K[j] = deltaRow * deltaRow.T 13 K = exp(K/(-1*kTup[1]**2)) 14 # kTup 元组值异常,抛出异常信息 15 else:raise NameError(\'Houston We Have a Problem --That Kernel is not recognized\') 16 return K
3 支持向量机预测分类测试结果
测试函数代码如下:
1 # 训练样本集的错误率和测试样本集的错误率 2 def testRbf(k1=1.3): 3 dataArr,labelArr = loadDataSet(\'testSetRBF.txt\') # 训练样本的提取 4 b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, (\'rbf\', k1)) # 计算得到截距和对偶因子 5 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() 6 svInd=nonzero(alphas.A>0)[0] # 对偶因子大于零的值,支持向量的点对应对偶因子 7 sVs=datMat[svInd] 8 labelSV = labelMat[svInd] 9 print "there are %d Support Vectors" % shape(sVs)[0] 10 m,n = shape(datMat) 11 errorCount = 0 12 # 对训练样本集的测试 13 for i in range(m): 14 kernelEval = kernelTrans(sVs,datMat[i,:],(\'rbf\', k1)) # 对象 i 的映射值 15 predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
