Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
For example:
A = [2,3,1,1,4], return true.
A = [3,2,1,0,4], return false.
Array Greedy
解法一
最開始考虑的是用递归求解,对于A=[2,3,1,1,4]这个数组,能够
从头開始遍历,假设对于上面的第一个元素2,能够前进两步,然后分别求两个数组A1=[3,1,1,4]和A2=[1,1,4]的结果,例如以下图:这样的方法能够求解出结果,可是从图中不难看出会有大量的反复,结果在leetCode中也显示超时
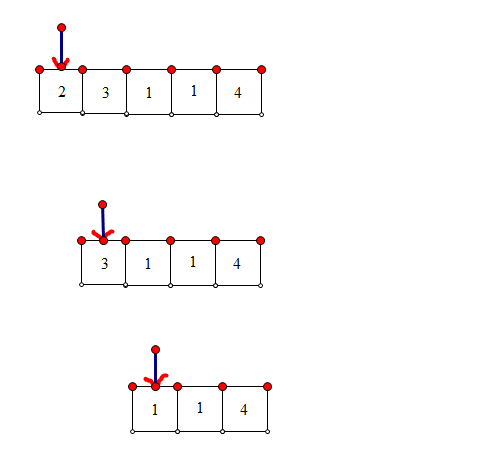
还是将代码列出:
class Solution {
public:
bool canJump(vector<int>& nums) {
int result=0;
canJumpChild(nums,0,result);
return result;
}
void canJumpChild(vector<int> & nums,int offset,int &result)
{
if(result==1)
return ;
if(offset==(nums.size()-1))
{
result=1;
return ;
}
vector<int>::iterator iter=nums.begin()+offset;
for(int i=1;i<=*iter;i++)
canJumpChild(nums,offset+i,result);
}
};然后看到了leetcode的提示greedy,就是说能够用贪婪算法来求解这个问题。发现这是一道很easy的用贪婪发就能够求解的,以下解法二和解法三都是这个思路。
解法二
贪婪策略依据还能向前移动的步长来推断,从第二个元素開始循环,假设能移动的步长小于等于0。表示无法到达这一步,就返回false。否则依据当前索引处的值来更新能移动的步长。代码例如以下:
class Solution {
public:
bool canJump(vector<int>& nums) {
//remain_step记录剩下的步数。表示最多能向前移动几步
int remain_step = nums.front();
//i能够理解成是否能到达的下标处。注意是从下标为1的位置開始,假设循环到数组的末端还能向前移动表示能到达末端
for(int i = 1; i<nums.size(); i++) {
//当这个值降低到0。无法进一步向前移动
if(remain_step <= 0) return false;
//更新这个值
remain_step = max(--remain_step, nums[i]);
}
return true;
}
};
解法三
贪婪策略是能到达的最远处,每次到达一个下标处后就更新能到达的最远处的值。
class Solution {
public:
bool canJump(vector<int>& nums) {
int max_jump=0;//max_jump表示能到达的最远的地方的下标。初始在0处
//跳出循环的条件是已经走到了最远处
for(int i=0;i<=max_jump;i++)//max_jump表示能到达的最远位置的下标
{
//假设能到达的最远位置的下标大于等于nums.size()-1。表示能到达末尾
if(max_jump>=nums.size()-1)
return true;
if(i+nums[i]>max_jump)
max_jump=i+nums[i];//更新能到达的最远的地方
}
return false;
}
};