莱布尼茨三角 与 杨辉三角 与排列组合 C=n!/[(n-m)!] . 它们三个的关系,

Posted 2023-04-13

参考技术A 是.
杨辉三角第n行第m个数,是C(m-1,n-1)
莱布尼茨三角的第n行乘以n的阶乘,就是杨辉三角的第n行
莱布尼茨三角的第n行第m个数,是C(m-1,n-1)/n!

算法零基础学习组合数与杨辉三角

文章目录

• 📖知识点回顾
• • 组合数
  • 杨辉三角
  • 杨辉三角和组合数之间的关系
• ✨练习：119. 杨辉三角
• • 问题描述
  • 提示
  • 方法一：逐层递推
  • • 优化：使用一维List实现
  • 方法二：线性递推

📖知识点回顾

组合数

百度百科
组合数表示的是 从 n 个不同元素中选取 m 个元素的方法的个数。
使用$$C_n^m$$进行表示。

杨辉三角

杨辉三角，又称帕斯卡三角。
在杨辉三角中，每一行的首尾都是1，而该行的其他元素等于上一行的两个相邻元素之和。如下图所示：

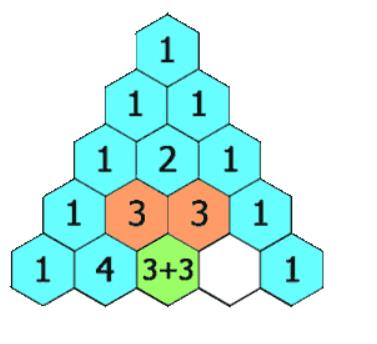
杨辉三角和组合数之间的关系

两者之间的关系，更加准确地讲，是 杨辉三角和组合数地递推公式 之间地关系。

1. 对于杨辉三角来说，对于第 i 行第 j 列的元素我们可以使用
   $$tar[i][j]=tar[i-1][j]+tar[i-1][j-1],i>=2$$
   $$tar[i][0]=tar[i][i]=1.$$
   进行表示。
2. 而组合数的递推公式是$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$如果写成函数形式的话，可以表示为

$$f(n,m)=f(n-1,m)+f(n-1,m-1)$$
这和杨辉三角的表示是一致的。

✨练习：119. 杨辉三角

指路：杨辉三角

问题描述

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

提示

` 0 <= rowIndex <= 33

示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

方法一：逐层递推

使用一个 二维数组 用于存储杨辉三角中每一层的数值。
但是使用一个 n*n 的数组太浪费空间，所以使用 List 进行存储。

class Solution 
    public List<List<Integer>> generate(int numRows) 
        List<List<Integer>> res = new ArrayList<>();
        
        for(int i = 0; i < numRows; ++i)
            List<Integer> arr = new ArrayList<>(i + 1);
            for(int j = 0; j < i + 1; ++j)
                if(j==0||j==i)
                    arr.add(1);
                else
                    arr.add( res.get(i-1).get(j-1)+res.get(i-1).get(j));
            
            res.add(arr);
        
        return res;
    

优化：使用一维List实现

优化缘由：杨辉三角中某一行的数值仅与 相邻的上一行 数值有关，与其他行的数值没有关系，所以只需要保存上一行的数值即可。

class Soultion
	public List<Integer> getRow(int rowIndex) 
		// 保存上一行的数据
		List<Integer> pre = new ArrayList<>();
		pre.add(1);
		for(int i = 0; i < rowIndex; ++i)
			List<Integer> cur = new ArrayList<>();//保存当前的数据
			cur.add(1);	//首元素
			for(int j = 1; j <= i; ++j)			//添加除首尾元素之外的数据
				cur.add(pre.get(j) + pre.get(j-1)); 
			
			cur.add(1);	//尾元素
			pre = cur;
		
		
		return pre;
	

方法二：线性递推

线性递推的原理：
$$C_n^m=C_n^{m-1}\ast \frac{n-m+1}{m}$$

class Solution 
    public List<Integer> getRow(int rowIndex) 
        List<Integer> row = new ArrayList<>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) 
            row.add((int) ((long) row.get(i - 1) * (rowIndex - i + 1) / i));
        
        return row;