一道备战noip的题目。不用完整程序，只要方法。

Posted 2023-04-13

题3 吃面包
【题目描述】
yk最近比较兴奋，因为有数学保送啦~ 如果noip2010他再拿一个保送的话，那么yk就拿了四个保送了！！（orz…）yk兴奋到梦里都在跳…
yk梦到自己来到N个面包做成的城堡前面（为什么是面包？？？因为yk喜欢吃面包呗…（yk注：其实yk不喜欢吃面包）），这N个面包城堡从左向右排成一列，每个面包城堡一个初始的高度，从左往右数第i个城堡的高度为A[i]。现在yk要从第1个跳到第N个城堡，但是yk比较懒，他只想不停地向上跳或者向下跳（平着跳也可以），但是不想一会儿向上跳，一会儿向下跳，否则yk的好心情会被破坏，所以他请jzj过来帮他吃掉一些面包或者盖上一些面包（可怜的jzj……），也就是让某些城堡的高度增加或者减少，以此满足yk快乐地跳城堡的心愿。
对于每一个面包城堡，jzj吃掉x个单位长度和盖上x个单位长度所耗费的力气都是x，jzj想花尽量少的力气帮yk完成心愿。也就是对于原来面包城堡高度为A_1，A_2，A_3…A_N，jzj通过耗费力气将面包城堡高度变为B_1,B_2,B_3…B_N，现在想在B数组不降或不升的前提下，|A_1 - B_1| + |A_2 - B_2| + ... + |A_N - B_N|最小。
【输入格式】
第1行: 输入1个整数：N
第2..N+1行: 第i+1行为1个整数：A_I
【输出格式】
第1行: 输出1个正整数，表示jzj为了帮助yk完成心愿所需要花费的最小力气。
【输入样例】bread.in
7
1
3
2
4
5
3
9
【输出样例】bread.out
3
【样例解释】：
jzj将第一个高度为3的城堡的吃掉一口变为2，将第二个高度为3的城堡盖上两层增加到5，花费的力气和为|2-3|+|5-3| = 3，并且每个城堡的高度为一个不下降序列1,2,2,4,5,5,9。
【数据规模】
100% N<=2000，0 <= A_i <= 1,000,000,000

首先，真正有意义的数字就那么2000个，因为我们每次都肯定是升到或者降到以前的某个数（这是废话）。所以离散化一下就好了。
第二，就是dp了，F[i,j]=minf[i-1,k]+|a[i]-a[k]| （a[k]>a[j]) 或者是（a[k]<a[j])必须一直保证。
F[i,j]表示的是如果将第i个楼梯搞成a[j]高的话，我们需要的最小力气。这题就解完了，但是时间不够，为O（n3）。
第三，就是优化了，我们发现，minf[i-1,k]是瓶颈，怎么办呢，把他预处理出来，g[i,j]=minf[i,k](k<j),这样时间为O(n2),这道题就完美解决了。
闲着无聊，瞎写的，有错误地方请指出，太明显的就自己理解好了。
还有这道是你们学校自己出着玩的吧，不应该出到第三题难度，第二题比较合适。题目别太水了。追问

预处理再细点吧。。

追答

g[i,j]=minf[i,k]这句话不懂吧，换句话说g[i,j]=min(f[i,j],g[i,j-1])这把明白了吗？

参考技术A 首先要看题目中的内存限制（08年是50MB，09年是128MB）
估计今年也会是128MB左右

其次，要知道每个类型变量所占空间
常用的：
integer占2字节
longint占4字节
real占6字节
qword占8字节
extended占10字节
string和ansistring大小由长度决定

然后通过定义变量中的大小估计程序所占内存大小
比如内存限制为128MB时
integer约能开60,000,000个
longint约能开30,000,000个
如果数组开得太大会导致内存溢出

至于动态的数组 如指针类型的变量
需要通过程序的空间复杂度来判断
如：
无项图中邻接表的空间大小约为边数*2
等

同时，递归也会占内存，
因此递归时层数不能多，
而且最好不要在过程中定义大数组，
将大数组当做参数带入时尽量写var当做变参使用
计算递归所占内存是一般是：
递归深度 * 过程中定义的变量和过程的值参 所占的内存

所以说，一般内存都是自己估计的，
因此在做题前需要判断好时间空间复杂度，
否则会出现TLE或OLE的情况

========================================
boolean占1个字节

应该是可以的 运行程序时不要开其他程序运行
任务管理器-性能-认可用量的总数看到了吗?
在刚开始运行时观察总数的变化

我已经测试过：
我开了1000 0000的longint 理论上空间是4000 0000字节，约40000KB
认可总量从67XXXX变为了71XXXX 还是比较准的

NOIP 装箱问题

题目：[NOIP2001]装箱问题 ，哈哈，我们今天来看一道很古老的题嘛，这是选自NOIP上的一道题，好了，我们一起来看看题意吧：

考虑到直接复制题目，或者截屏的方式不是很方便阅读，我就把直接题目链接放下面！
题目传送门： [NOIP2001]装箱问题

思路:

写过01背包的老板看到这道题时，嘴角微微上扬，说，这还不简单,分分钟AC😎

但是,我这里用另一种动态规划的思路

先说说为什么要用动态规划吧：如果用暴力法的话（枚举每个物品装箱还是不装箱），时间复杂度会很高 O(2^n) 😗, 我们需要降低时间复杂度。

举个例子：背包容量 20， 5个物品，体积分别为，1,2,2,4,5 ，若我们枚举每个物品放不放的话，时间复杂度是 2^5 ，我们思考下，可以发现我们放两个体积为2的物品和放一个体积为4的物品，对结果是没有影响的。 我们算出这些物品可以放出的体积有： 1,2,3,4,5,6,7,8,9,10,11,12,13,14 这里一共14次（不排除算错的可能哈😂），而暴力法的话，有32种情况。

我们采用动态规划的思想呢，时间复杂度为：物品个数*背包体积

我们来看看成功AC的代码吧：

二维数组版

#include<bits/stdc++.h>
using namespace std;
int n,total;
int v[20010];
int f[35][20010];
int main()
    f[0][0]=1;
    cin>>total>>n;
    for(int i=1;i<=n;i++) cin>>v[i];
    /**
     * f[i][j] 表示 0到i 的物品能否填满容量为 j 的背包
     */
     for(int i=1;i<=n;i++)
         for(int j=0;j<=total;j++)
             // f[i-1][j] 就表示前面 i-1 件物品能否填满容量为j的背包
             // f[i-1][j-v[i]] 表示前面 i-1 件物品能否填满容量为j-v[i]的背包
             if(j>=v[i]) f[i][j]=f[i-1][j]||f[i-1][j-v[i]];
             else f[i][j]=f[i-1][j];
         
     
     int ans=0;
     for(int i=total;i>=0;i--)
         if(f[n][i]==1)
             ans = i;break;
         
     
     cout<<total-ans;
    return 0;

我这里放一张雨巨的图，便于大家理解

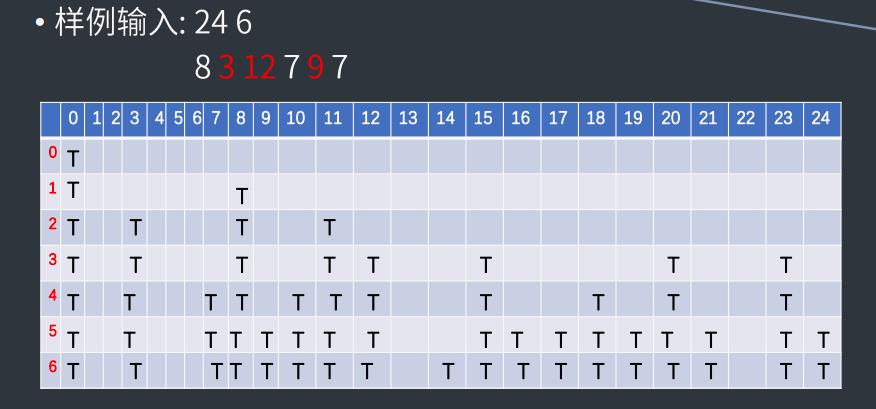
我们可以看到每一行的结果实际上只与上一行有关，所以啊，我们可以压缩一下

压缩时有个坑：我们遍历体积的时候，需要从大到小去遍历，这样是为了防止让一个物品多次放入背包（这波操作真的很有意思😜）

下面我直接放代码

一维数组版

#include<bits/stdc++.h>
using namespace std;
int n,total;
int v[20010];
int f[20010];
int main()
    f[0]=1;
    cin>>total>>n;
    for(int i=1;i<=n;i++) cin>>v[i];
    for(int i=1;i<=n;i++)
         for(int j=total;j>=v[i];j--)
             f[j]=f[j]||f[j-v[i]];
         
     
     int ans=0;
     for(int i=total;i>=0;i--)
         if(f[i]==1)
             ans = i;break;
         
     
     cout<<total-ans;
    return 0;

谢谢你的阅读，希望能够帮助你更好的理解动态规划,由于作者水平有限，也难免有不足之处，若读者发现问题，还请批评，在留言区留言或者私信告知，我一定会尽快修改的。若各位大佬有什么好的解法，或者有意义的解法都可以在评论区展示额，万分谢谢。
写作不易，各位老板的肯定和关注都是我坚持下去的动力😘