数据结构拓扑排序序列

Posted 2023-04-10

写出下图的三种不同拓扑排序序列。

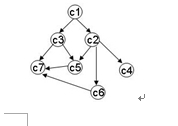
拓扑排序序列有6种。先找到第一个没有被指的，就是C1，加入序列。然后擦掉跟C1有关的边，此时C2和C3都满足没有被指，选一个，比如选C2，加入序列，擦掉和C2有关的边，这个时候可以选C3,C4,C5或C6，如此而已。

数据结构拓扑排序实际上是离散数学中的概念。

这里不打算说太多形式化的定义，形式化的定义教科书上或者上面给的链接中就说的很详细。还是以上面选课的例子来描述这两个概念。假设我们在学习完了算法这门课后，可以选修机器学习或者计算机图形学。这个或者表示，学习机器学习和计算机图形学这两门课之间没有特定的先后顺序。

因此，在我们所有可以选择的课程中，任意两门课程之间的关系要么是确定的(即拥有先后关系)，要么是不确定的(即没有先后关系)，绝对不存在互相矛盾的关系(即环路)。以上就是偏序的意义，抽象而言，有向图中两个顶点之间不存在环路，至于连通与否，是无所谓的。所以，有向无环图必然是满足偏序关系的。

理解了偏序的概念，那么全序就好办了。所谓全序，就是在偏序的基础之上，有向无环图中的任意一对顶点还需要有明确的关系(反映在图中，就是单向连通的关系，注意不能双向连通，那就成环了)。

可见，全序就是偏序的一种特殊情况。回到我们的选课例子中，如果机器学习需要在学习了计算机图形学之后才能学习(可能学的是图形学领域相关的机器学习算法……)，那么它们之间也就存在了确定的先后顺序，原本的偏序关系就变成了全序关系。 

实际上，很多地方都存在偏序和全序的概念。比如对若干互不相等的整数进行排序，最后总是能够得到唯一的排序结果(从小到大，下同)。这个结论应该不会有人表示疑问吧:)但是如果我们以偏序/全序的角度来考虑一下这个再自然不过的问题，可能就会有别的体会了。

拓展到拓扑排序中，结果具有唯一性的条件也是其所有顶点之间都具有全序关系。如果没有这一层全序关系，那么拓扑排序的结果也就不是唯一的了。在后面会谈到，如果拓扑排序的结果唯一，那么该拓扑排序的结果同时也代表了一条哈密顿路径。

参考技术A

对一个有向无环图简称G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u，v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序的序列，简称拓扑序列。

由拓扑序列的生成方法的出图中三种不同拓扑排序的序列：第一种：c1、c2、c4、c3、c5、c6，第二种：c1、c2、c4、c3、c6、c5，第三种：c1、c3、c2、c4、c5、c6。

扩展资料：

拓扑排序执行步骤

由AOV网构造拓扑序列的拓扑排序算法主要是循环执行以下两步，直到不存在入度为0的顶点为止。

 首先选择一个入度为0的顶点并输出之。

 从网中删除此顶点和所有出边。

循环结束后，若输出的顶点数小于网中的顶点数，则输出“有回路”信息，否则输出的顶点序列就是一种拓扑序列。

参考资料来源：百度百科-拓扑排序

参考技术B 拓扑排序的方法是，先找到第一个没有被指的，就是C1，加入序列。然后擦掉跟C1有关的边，此时C2和C3都满足没有被指，选一个，比如选C2，加入序列，擦掉和C2有关的边，这个时候可以选C3,C4,C5或C6……如此而已 参考技术C 1,2,3,4,5,6,7
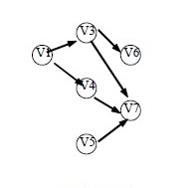
1,2,3,5,6,7,4
1,3,2,4,5,6,7
拓扑序列就是从没有箭头指的那个开始，下一个必须也没有被箭头指（这个叫什么不记得了）。。 参考技术D 一：c1,c2,c3,c4,c5,c6,c7
二：c1,c2,c4,c6,c3,c5,c7
三：c1,c3,c2,c5,c6,c4,c7

拓扑排序+关键路径

参考技术A

有向无环图DAG
顶点表示活动的网络AOV网：用DAG图表示一个工程，其顶点表示活动，有向边<vi,vj>表示活动vi必须先于活动vj进行
拓扑排序（由一个有向无环图的顶点组成的序列）
1.每个顶点出现且仅出现一次
2.若顶点A在序列中排在顶点B之前，则图中不存在B到A的路径
每个DAG图都有一个或多个拓扑排序序列。
若一个顶点有多个直接后继，则拓扑排序的结果通常不唯一；但若各个顶点已经排在一个线性有序序列中，每个顶点有唯一的前驱后继关系，再做拓扑排序时，则排序结果是唯一的。
若邻接矩阵是三角矩阵的话拓扑排序一定存在，反之不一定。
步骤
1.从DAG图中选择一个没有前驱的顶点并输出（必须在它之前进行大的活动已经都完成了）
2.从图中删除该顶点和所有以它为起点的有向边
3.重复1，2直到当前的DAG图为空或当前图中不存在无前驱的结点为止。后者说明有环。

栈

时间复杂度O(|V|+|E|)
用深度优先遍历也可以实现拓扑排序
若已知无环图，则可用拓扑排序来改进Dijkstra算法
以拓扑顺序来选取顶点，运行时间为O(|E|+|V|)

用边表示活动的网络AOE网：在带权有向图中，以顶点表示事件，有向边表示活动，以边上的权值表示完成该活动的开销。
1.只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始。
2.只有在进入某一顶点的各有向边所代表的活动都已结束，该顶点所代表的事件才能发生。
仅有一个入度为0的顶点，称为开始顶点（源点），表示整个工程的开始。仅有一个出度为0的顶点，结束结点（汇点），表示整个工程的结束。
有些活动是可以并行进行的
从源点都汇点的路径可能有多条，所有路径上的活动都完成了整个工程才算结束，所以把路径长度最大的称为 关键路径 ，其上的活动称为 关键活动 。完成整个工程的最短时间就是关键路径的长度。关键活动不能按时完成，则整个工程的完成时间都会受到影响。
事件Vk的最早发生时间Ve(k)
从开始顶点V到Vk的最长路径长度
Ve(V)=0
Ve(k)=MaxVe(j)+Weight(Vj, Vk)
从前往后计算
事件Vk的最迟发生时间Vl(k)
在不推迟整个工程完成的前提下，即保证它所指向的时间Vi在Ve(i)时刻能够发生时，该事件最迟必须发生的时间。
Vl(汇点)=Ve(汇点)
Vl(j)=MinVl(k)-Weight(Vj, vk)
从后往前计算
活动Ai的最早开始时间E(i)
等于该活动的起点所表示的事件的最早发生时间
活动Ai的最迟开始时间L(i)
等于该活动的终点所表示的事件的最迟发生时间减去该活动所需要的时间
活动Ai可以拖延的时间D(i)
其最早开始时间与最迟开始时间的差值
若为0的话，就代表该活动必须要如期完成，否则会拖延完成整个工程的进度，则该活动是关键活动。