[LeetCode] 208. Implement Trie (Prefix Tree) 实现字典树(前缀树)

Posted 2020-10-26 轻风舞动

Implement a trie with insert, search, and startsWith methods.

Example:

Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true
trie.insert("app");   
trie.search("app");     // returns true

Note:

• You may assume that all inputs are consist of lowercase letters a-z.
• All inputs are guaranteed to be non-empty strings.

实现一个数据结构：字典树(前缀树或单词查找树)，具备insert, search, startsWith的功能。参考董的博客：数据结构之Trie树

Trie树，又称字典树，单词查找树或者前缀树，是一种用于快速检索的多叉树结构，如英文字母的字典树是一个26叉树，数字的字典树是一个10叉树。Trie树可以利用字符串的公共前缀来节约存储空间。

Trie树的基本性质可以归纳为：

（1）根节点不包含字符，除根节点以外每个节点只包含一个字符。

（2）从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

（3）每个节点的所有子节点包含的字符串不相同。

下图是一个保存了8个键的trie结构，"A", "to", "tea", "ted", "ten", "i", "in", and "inn"

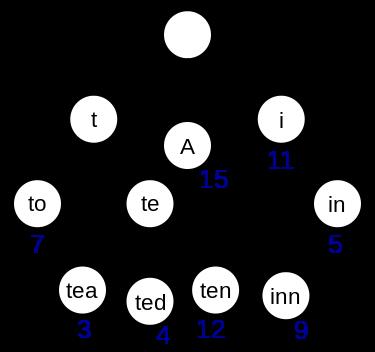
Trie树复杂度:

（1）插入、查找的时间复杂度均为O(n)，其中n为字符串长度。

（2) 空间复杂度是26^n级别的，非常庞大（可采用双数组实现改善）。

实施方法：因为只用26个字母，所以可以用数组记录，数组元素为TrieNode。

 

Java:

class TrieNode {
    private TrieNode[] children;
    public boolean hasWord;
    
    // Initialize your data structure here.
    public TrieNode() {
        children = new TrieNode[26];
        hasWord = false;
    }
    
    public void insert(String word, int index) {
        if (index == word.length()) {
            this.hasWord = true;
            return;
        }
        
        int pos = word.charAt(index) - \'a\';
        if (children[pos] == null) {
            children[pos] = new TrieNode();
        }
        children[pos].insert(word, index + 1);
    }
    
    public TrieNode find(String word, int index) {
        if (index == word.length()) {
            return this;
        }
        
        int pos = word.charAt(index) - \'a\';
        if (children[pos] == null) {
            return null;
        }
        return children[pos].find(word, index + 1);
    }
}

public class Trie {
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    // Inserts a word into the trie.
    public void insert(String word) {
        root.insert(word, 0);
    }

    // Returns if the word is in the trie.
    public boolean search(String word) {
        TrieNode node = root.find(word, 0);
        return (node != null && node.hasWord);
    }

    // Returns if there is any word in the trie
    // that starts with the given prefix.
    public boolean startsWith(String prefix) {
        TrieNode node = root.find(prefix, 0);
        return node != null;
    }
}　

Python:  Time: O(n), per operation,  Space: O(1)

class TrieNode:
  def __init__(self):
    # Initialize your data structure here.
    self.childs = dict()
    self.isWord = False

class Trie:
  def __init__(self):
    self.root = TrieNode()

  # @param {string} word
  # @return {void}
  # Inserts a word into the trie.
  def insert(self, word):
    node = self.root
    for letter in word:
      child = node.childs.get(letter)
      if child is None:
        child = TrieNode()
        node.childs[letter] = child
      node = child
    node.isWord = True

  # @param {string} word
  # @return {boolean}
  # Returns if the word is in the trie.
  def search(self, word):
    node = self.root
    for letter in word:
      node = node.childs.get(letter)
      if node is None:
        return False
    return node.isWord

  # @param {string} prefix
  # @return {boolean}
  # Returns if there is any word in the trie
  # that starts with the given prefix.
  def startsWith(self, prefix):
    node = self.root
    for letter in prefix:
      node = node.childs.get(letter)
      if node is None:
        return False
    return True　

Python:

class TrieNode:
    def __init__(self):
        self.is_string = False
        self.leaves = {}
        

class Trie:

    def __init__(self):
        self.root = TrieNode()

    def insert(self, word):
        cur = self.root
        for c in word:
            if not c in cur.leaves:
                cur.leaves[c] = TrieNode()
            cur = cur.leaves[c]
        cur.is_string = True

    def search(self, word):
        node = self.childSearch(word)
        if node:
            return node.is_string
        return False        

    def startsWith(self, prefix):
        return self.childSearch(prefix) is not None

    def childSearch(self, word):
        cur = self.root
        for c in word:
            if c in cur.leaves:
                cur = cur.leaves[c]
            else:
                return None
        return cur

C++:

class TrieNode {
public:
    // Initialize your data structure here.
    TrieNode() : is_string(false) {
        
    }
    bool is_string;
    unordered_map<char, TrieNode *> leaves;
};

class Trie {
public:
    Trie() {
        root_ = new TrieNode();
    }

    void insert(string word) {
        auto *cur = root_;
        for (const auto& c : word) {
            if (!cur->leaves.count(c)) {
                cur->leaves[c] = new TrieNode();
            }
            cur = cur->leaves[c];
        }
        cur->is_string = true;
    }

    bool search(string word) {
        auto *node = childSearch(word);
        if (node) {
            return node->is_string;
        }
        return false;   
    }

    bool startsWith(string prefix) {
        return childSearch(prefix);
    }

    TrieNode *childSearch(const string& word) {
        auto *cur = root_;
        for (const auto& c : word) {
            if (cur->leaves.count(c)) {
                cur = cur->leaves[c];
            } else {
                return nullptr;
            }
        }
        return cur;
    }

private:
    TrieNode *root_;
};

　

All LeetCode Questions List 题目汇总