一文详解8种异常检测算法(附Python代码)
Posted Python数据开发
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了一文详解8种异常检测算法(附Python代码)相关的知识,希望对你有一定的参考价值。
文章目录
一、异常检测简介
异常检测是通过数据挖掘方法发现与数据集分布不一致的异常数据,也被称为离群点、异常值检测等等。
1.1 异常检测适用的场景
异常检测算法适用的场景特点有:(1)无标签或者类别极不均衡;(2)异常数据跟样本中大多数数据的差异性较大;(3)异常数据在总体数据样本中所占的比例很低。常见的应用案例如:
金融领域:从金融数据中识别”欺诈用户“,如识别信用卡申请欺诈、信用卡盗刷、信贷欺诈等;安全领域:判断流量数据波动以及是否受到攻击等等;电商领域:从交易等数据中识别”恶意买家“,如羊毛党、恶意刷屏团伙;生态灾难预警:基于天气指标数据,判断未来可能出现的极端天气;医疗监控:从医疗设备数据,发现可能会显示疾病状况的异常数据;
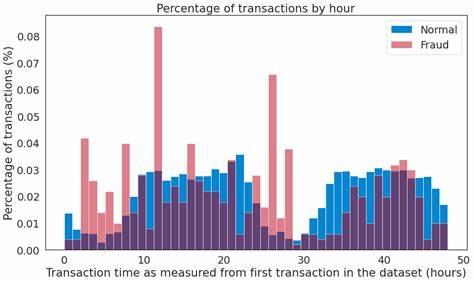
1.2 异常检测存在的挑战
异常检测是热门的研究领域,但由于异常存在的未知性、异质性、特殊性及多样性等复杂情况,整个领域仍有较多的挑战:
1)最具挑战性的问题之一是难以实现高异常检测召回率。由于异常非常罕见且具有异质性,因此很难识别所有异常。
2)异常检测模型要提高精确度(precision)往往要深度结合业务特征,否则效果不佳,且容易导致对少数群体产生算法偏见。
二、异常检测方法
按照训练集是否包含异常值可以划分为异常值检测(outlier detection)及新颖点检测(novelty detection),新颖点检测的代表方法如one class SVM。
按照异常类别的不同,异常检测可划分为:异常点检测(如异常消费用户),上下文异常检测(如时间序列异常),组异常检测(如异常团伙)。
按照学习方式的不同,异常检测可划分为:有监督异常检测(Supervised Anomaly Detection)、半监督异常检测(Semi-Supervised Anomaly Detection)及无监督异常检测(Unsupervised Anomaly Detection)。现实情况的异常检测问题,由于收集异常标签样本的难度大,往往是没有标签的,所以无监督异常检测应用最为广泛。
无监督异常检测按其算法思想大致可分为如下下几类:
2.1 基于聚类的方法
基于聚类的异常检测方法通常依赖下列假设,1)正常数据实例属于数据中的一个簇,而异常数据实例不属于任何簇;2)正常数据实例靠近它们最近的簇质心,而异常数据离它们最近的簇质心很远;3)正常数据实例属于大而密集的簇,而异常数据实例要么属于小簇,要么属于稀疏簇;通过将数据归分到不同的簇中,异常数据则是那些属于小簇或者不属于任何一簇或者远离簇中心的数据。
-
将距离簇中心较远的数据作为异常点:这类方法有 SOM、K-means、最大期望( expectation maximization,EM)及基于语义异常因子( semantic anomaly factor)算法等;
-
将聚类所得小簇数据作为异常点:代表方法有K-means聚类;
-
将不属于任何一簇作为异常点:代表方法有 DBSCAN、ROCK、SNN 聚类。
2.2 基于统计的方法
基于统计的方法依赖的假设是数据集服从某种分布( 如正态分布、泊松分布及二项式分布等) 或概率模型,通过判断某数据点是否符合该分布/模型( 即通过小概率事件的判别) 来实现异常检测。根据概率模型可分为:
1)参数方法,由已知分布的数据中估计模型参数( 如高斯模型) ,其中最简单的参数异常检测模型就是假设样本服从一元正态分布,当数据点与均值差距大于两倍或三倍方差时,则认为该点为异常;
2)非参数方法,在数据分布未知时,可绘制直方图通过检测数据是否在训练集所产生的直方图中来进行异常检测。还可以利用数据的变异程度( 如均差、标准差、变异系数、四分位数间距等) 来发现数据中的异常点数据。
2.3 基于深度的方法
该方法将数据映射到 k 维空间的分层结构中,并假设异常值分布在外围,而正常数据点靠近分层结构的中心(深度越高)。
-
半空间深度法( ISODEPTH 法) ,通过计算每个点的深度,并根据深度值判断异常数据点。
-
最小椭球估计 ( minimum volume ellipsoid estimator,MVE)法。根据大多数数据点( 通常为 > 50% ) 的概率分布模型拟合出一个实线椭圆形所示的最小椭圆形球体的边界,不在此边界范围内的数据点将被判断为异常点。
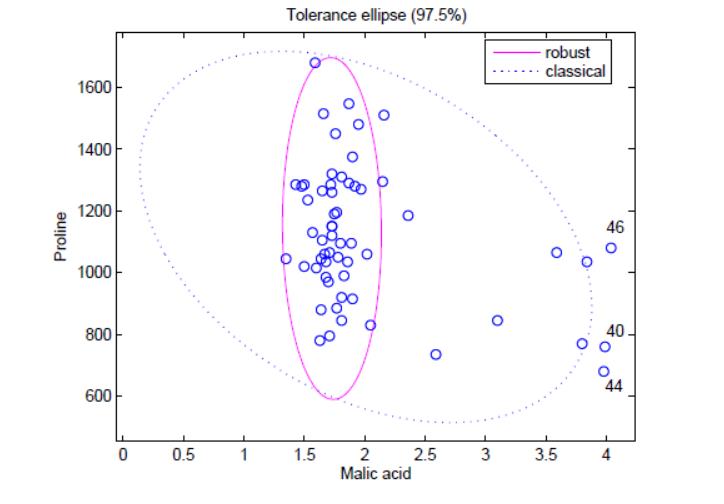
- 孤立森林。上述两种基于深度的基础模型随着特征维度k的增加,其时间复杂性呈指数增长,通常适用于维度k≤3 时,而孤立森林通过改变计算深度的方式,也可以适用于高维的数据。
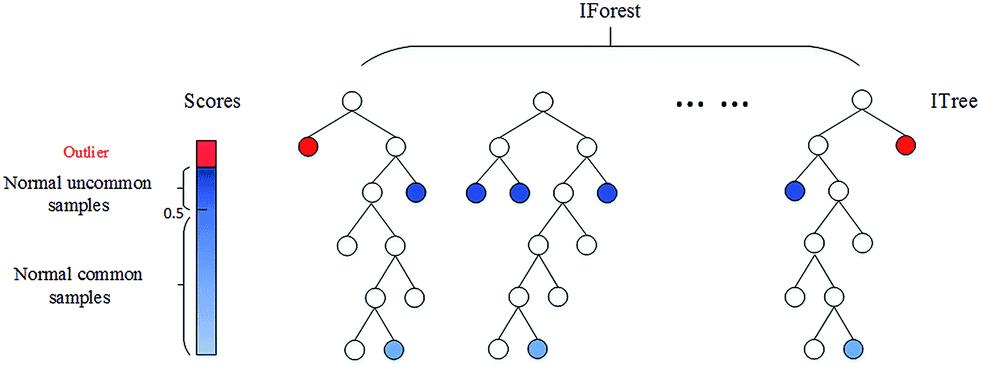
孤立森林算法是基于 Ensemble 的异常检测方法,因此具有线性的时间复杂度。且精准度较高,在处理大数据时速度快,所以目前在工业界的应用范围比较广。其基本思想是:通过树模型方法随机地切分样本空间,那些密度很高的簇要被切很多次才会停止切割(即每个点都单独存在于一个子空间内),但那些分布稀疏的点(即异常点),大都很早就停到一个子空间内了。算法步骤为:
1)从训练数据中随机选择 Ψ 个样本,以此训练单棵树。
2)随机指定一个q维度(attribute),在当前节点数据中随机产生一个切割点p。p切割点产生于当前节点数据中指定q维度的最大值和最小值之间。
3)在此切割点的选取生成了一个超平面,将当前节点数据空间切分为2个子空间:把当前所选维度下小于 p 的点放在当前节点的左分支,把大于等于 p 的点放在当前节点的右分支;
4)在节点的左分支和右分支节点递归步骤 2、3,不断构造新的叶子节点,直到叶子节点上只有一个数据(无法再继续切割) 或树已经生长到了所设定的高度 。(设置单颗树的最大高度是因为异常数据记录都比较少,其路径长度也比较低,而我们也只需要把正常记录和异常记录区分开来,因此只需要关心低于平均高度的部分就好,这样算法效率更高。)
5)由于每颗树训练的切割特征空间过程是完全随机的,所以需要用 ensemble 的方法来使结果收敛,即多建立几棵树,然后综合计算每棵树切分结果的平均值。对于每个样本 x,通过下面的公式计算综合的异常得分s。

h(x) 为 x 在每棵树的高度,c(Ψ) 为给定样本数 Ψ 时路径长度的平均值,用来对样本 x 的路径长度 h(x) 进行标准化处理。
2.4 基于分类模型
代表方法是One class SVM,其原理是寻找一个超平面将样本中的正例圈出来,预测就是用这个超平面做决策,在圈内的样本就认为是正样本。由于核函数计算比较耗时,在海量数据的场景用的并不多。
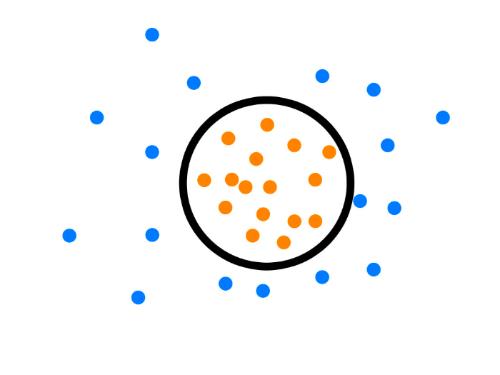
依赖的假设是:正常数据实例位于密集的邻域中,而异常数据实例附近的样例较为稀疏。可以继续细分为 基于密度/邻居:
-
基于密度,该方法通过计算数据集中各数据区域的密度,将密度较低区域作为离群区域。经典的方法为:局部离群因子( local outlier factor,LOF) 。LOF 法与传统异常点非彼即此定义不同,将异常点定义局域是异常点,为每个数据赋值一个代表相对于其邻域的 LOF 值,LOF 越大,说明其邻域密度较低,越有可能是异常点。但在 LOF 中难以确定最小近邻域,且随着数据维度的升高,计算复杂度和时间复杂度增加。
-
基于距离,其基本思想是通过计算比较数据与近邻数据集合的距离来检测异常,正常数据点与其近邻数据相似,而异常数据则有别于近邻数据。
2.6 基于偏差的方法
当给定一个数据集时,可通过基于偏差法找出与整个数据集特征不符的点,并且数据集方差会随着异常点的移除而减小。该方法可分为逐个比较数据点的序列异常技术和 OLAP 数据立方体技术。目前该方法实际应用较少。
2.7 基于重构的方法
代表方法为PCA。PCA在异常检测方面的做法,大体有两种思路:一种是将数据映射到低维特征空间,然后在特征空间不同维度上查看每个数据点跟其它数据的偏差;另外一种是将数据映射到低维特征空间,然后由低维特征空间重新映射回原空间,尝试用低维特征重构原始数据,看重构误差的大小。
2.8 基于神经网络的方法
代表方法有自动编码器( autoencoder,AE) ,长短期记忆神经网络(LSTM)等。
-
LSTM可用于时间序列数据的异常检测:利用历史序列数据训练模型,检测与预测值差异较大的异常点。
-
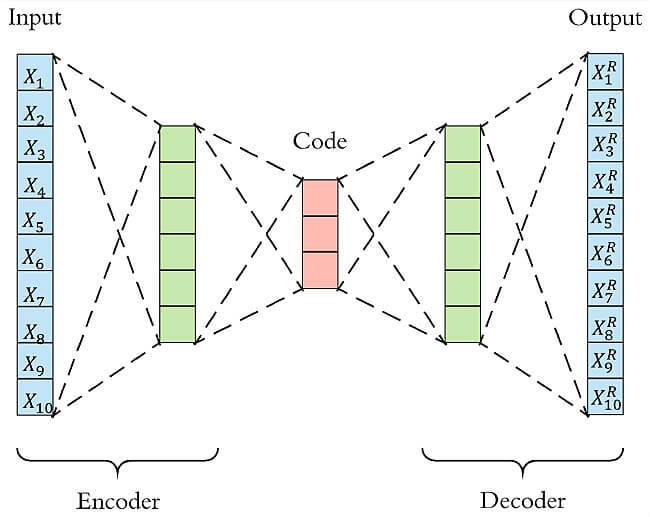
Autoencoder异常检测 Autoencoder本质上使用了一个神经网络来产生一个高维输入的低维表示。Autoencoder与主成分分析PCA类似,但是Autoencoder在使用非线性激活函数时克服了PCA线性的限制。算法的基本上假设是异常点服从不同的分布。根据正常数据训练出来的Autoencoder,能够将正常样本重建还原,但是却无法将异于正常分布的数据点较好地还原,导致其基于重构误差较大。当重构误差大于某个阈值时,将其标记为异常值。
小结:无监督异常检测方法的要素为选择相关的特征以及基于合理假设选择合适的算法,可以更好的发挥异常检测效果。
技术交流
技术要学会分享、交流,不建议闭门造车。
本文技术由粉丝群小伙伴推荐、讨论、分享汇总。有趣使用工具、源码、数据、技术交流提升,均可加交流群获取,群友已超过3000人,添加时最好的备注方式为:来源+兴趣方向,方便找到志同道合的朋友。
方式①、添加微信号:dkl88191,备注:来自CSDN +技术交流
方式②、微信搜索公众号:Python学习与数据挖掘,后台回复:加群
三、项目实战:信用卡反欺诈
项目为kaggle上经典的信用卡欺诈检测,该数据集质量高,正负样本比例非常悬殊。我们在此项目主要用了无监督的Autoencoder新颖点检测,根据重构误差识别异常欺诈样本。
#!/usr/bin/env python
# coding: utf-8
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
import pickle
import matplotlib.pyplot as plt
plt.style.use('seaborn')
import tensorflow as tf
import seaborn as sns
from sklearn.model_selection import train_test_split
from keras.models import Model, load_model
from keras.layers import Input, Dense
from keras.callbacks import ModelCheckpoint
from keras import regularizers
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_curve, auc, precision_recall_curve
# 安利一个异常检测Python库 https://github.com/yzhao062/Pyod
# 读取数据 :信用卡欺诈数据集地址https://www.kaggle.com/mlg-ulb/creditcardfraud
d = pd.read_csv('creditcard.csv')
# 查看样本比例
num_nonfraud = np.sum(d['Class'] == 0)
num_fraud = np.sum(d['Class'] == 1)
plt.bar(['Fraud', 'non-fraud'], [num_fraud, num_nonfraud], color='dodgerblue')
plt.show()
# 删除时间列,对Amount进行标准化
data = d.drop(['Time'], axis=1)
data['Amount'] = StandardScaler().fit_transform(data[['Amount']])
# 为无监督新颖点检测方法,只提取负样本,并且按照8:2切成训练集和测试集
mask = (data['Class'] == 0)
X_train, X_test = train_test_split(data[mask], test_size=0.2, random_state=0)
X_train = X_train.drop(['Class'], axis=1).values
X_test = X_test.drop(['Class'], axis=1).values
# 提取所有正样本,作为测试集的一部分
X_fraud = data[~mask].drop(['Class'], axis=1).values
# 构建Autoencoder网络模型
# 隐藏层节点数分别为16,8,8,16
# epoch为5,batch size为32
input_dim = X_train.shape[1]
encoding_dim = 16
num_epoch = 5
batch_size = 32
input_layer = Input(shape=(input_dim, ))
encoder = Dense(encoding_dim, activation="tanh",
activity_regularizer=regularizers.l1(10e-5))(input_layer)
encoder = Dense(int(encoding_dim / 2), activation="relu")(encoder)
decoder = Dense(int(encoding_dim / 2), activation='tanh')(encoder)
decoder = Dense(input_dim, activation='relu')(decoder)
autoencoder = Model(inputs=input_layer, outputs=decoder)
autoencoder.compile(optimizer='adam',
loss='mean_squared_error',
metrics=['mae'])
# 模型保存为model.h5,并开始训练模型
checkpointer = ModelCheckpoint(filepath="model.h5",
verbose=0,
save_best_only=True)
history = autoencoder.fit(X_train, X_train,
epochs=num_epoch,
batch_size=batch_size,
shuffle=True,
validation_data=(X_test, X_test),
verbose=1,
callbacks=[checkpointer]).history
# 画出损失函数曲线
plt.figure(figsize=(14, 5))
plt.subplot(121)
plt.plot(history['loss'], c='dodgerblue', lw=3)
plt.plot(history['val_loss'], c='coral', lw=3)
plt.title('model loss')
plt.ylabel('mse'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
plt.subplot(122)
plt.plot(history['mae'], c='dodgerblue', lw=3)
plt.plot(history['val_mae'], c='coral', lw=3)
plt.title('model mae')
plt.ylabel('mae'); plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper right')
# 读取模型
autoencoder = load_model('model.h5')
# 利用autoencoder重建测试集
pred_test = autoencoder.predict(X_test)
# 重建欺诈样本
pred_fraud = autoencoder.predict(X_fraud)
# 计算重构MSE和MAE误差
mse_test = np.mean(np.power(X_test - pred_test, 2), axis=1)
mse_fraud = np.mean(np.power(X_fraud - pred_fraud, 2), axis=1)
mae_test = np.mean(np.abs(X_test - pred_test), axis=1)
mae_fraud = np.mean(np.abs(X_fraud - pred_fraud), axis=1)
mse_df = pd.DataFrame()
mse_df['Class'] = [0] * len(mse_test) + [1] * len(mse_fraud)
mse_df['MSE'] = np.hstack([mse_test, mse_fraud])
mse_df['MAE'] = np.hstack([mae_test, mae_fraud])
mse_df = mse_df.sample(frac=1).reset_index(drop=True)
# 分别画出测试集中正样本和负样本的还原误差MAE和MSE
markers = ['o', '^']
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']
plt.figure(figsize=(14, 5))
plt.subplot(121)
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp.index,
temp['MAE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.title('Reconstruction MAE')
plt.ylabel('Reconstruction MAE'); plt.xlabel('Index')
plt.subplot(122)
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp.index,
temp['MSE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.legend(loc=[1, 0], fontsize=12); plt.title('Reconstruction MSE')
plt.ylabel('Reconstruction MSE'); plt.xlabel('Index')
plt.show()
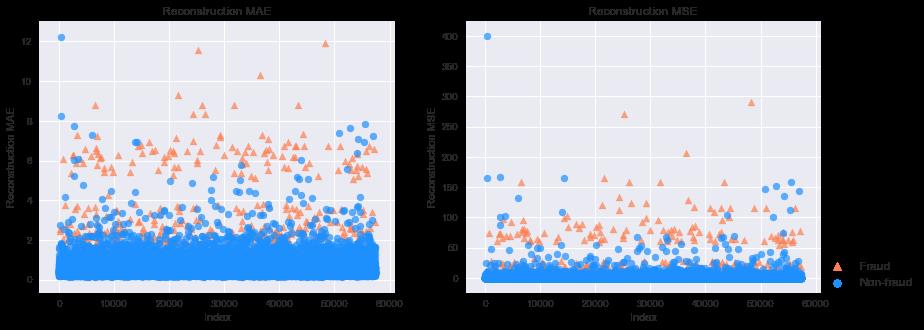
# 下图分别是MAE和MSE重构误差,其中橘黄色的点是信用欺诈,也就是异常点;蓝色是正常点。我们可以看出异常点的重构误差整体很高。
# 画出Precision-Recall曲线
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
plt.subplot(1, 2, i+1)
precision, recall, _ = precision_recall_curve(mse_df['Class'], mse_df[metric])
pr_auc = auc(recall, precision)
plt.title('Precision-Recall curve based on %s\\nAUC = %0.2f'%(metric, pr_auc))
plt.plot(recall[:-2], precision[:-2], c='coral', lw=4)
plt.xlabel('Recall'); plt.ylabel('Precision')
plt.show()
# 画出ROC曲线
plt.figure(figsize=(14, 6))
for i, metric in enumerate(['MAE', 'MSE']):
plt.subplot(1, 2, i+1)
fpr, tpr, _ = roc_curve(mse_df['Class'], mse_df[metric])
roc_auc = auc(fpr, tpr)
plt.title('Receiver Operating Characteristic based on %s\\nAUC = %0.2f'%(metric, roc_auc))
plt.plot(fpr, tpr, c='coral', lw=4)
plt.plot([0,1],[0,1], c='dodgerblue', ls='--')
plt.ylabel('TPR'); plt.xlabel('FPR')
plt.show()
# 不管是用MAE还是MSE作为划分标准,模型的表现都算是很好的。PR AUC分别是0.51和0.44,而ROC AUC都达到了0.95。
# 画出MSE、MAE散点图
markers = ['o', '^']
colors = ['dodgerblue', 'coral']
labels = ['Non-fraud', 'Fraud']
plt.figure(figsize=(10, 5))
for flag in [1, 0]:
temp = mse_df[mse_df['Class'] == flag]
plt.scatter(temp['MAE'],
temp['MSE'],
alpha=0.7,
marker=markers[flag],
c=colors[flag],
label=labels[flag])
plt.legend(loc=[1, 0])
plt.ylabel('Reconstruction RMSE'); plt.xlabel('Reconstruction MAE')
plt.show()
计算机视觉教程3-1:全面详解图像边缘检测算法(附Python实战)

目录
0 写在前面
从本节开始,计算机视觉教程进入第三章节——图像特征提取。在本章,你会见到一张简简单单的图片中蕴含着这么多你没注意到的细节特征,而这些特征将会在今后更高级的应用中发挥着极其重要的作用。本文讲解基础特征之一——图像边缘。
本文采用面向对象设计,定义了一个边缘检测类EdgeDetect,使图像边缘检测算法的应用更简洁,例如
import cv2
import numpy as np
import matplotlib.pyplot as plt
Detector = EdgeDetect('1.jpg')
Prewitt = Detector.prewitt()
plt.imshow(Prewitt , 'gray')
plt.show()
这个类的构造函数为
class EdgeDetect:
def __init__(self, img) -> None:
self.src = cv2.imread(img)
self.gray = cv2.cvtColor(self.src, cv2.COLOR_BGR2GRAY)
读取的是图像的基本信息。
1 一阶微分算子
图像边缘是数字图像的高频成分,对应图像梯度的极值。在二维离散数字图像上,某个方向上图像强度函数微分使用有限差分法来近似,即:
∂ f ∂ x [ i , j ] ≈ f [ i + 1 , j ] − f [ i , j ] ∂ f ∂ y [ i , j ] ≈ f [ i , j + 1 ] − f [ i , j ] \\begincases \\frac\\partial f\\partial x\\left[ i,j \\right] \\approx f\\left[ i+1,j \\right] -f\\left[ i,j \\right]\\\\ \\frac\\partial f\\partial y\\left[ i,j \\right] \\approx f\\left[ i,j+1 \\right] -f\\left[ i,j \\right]\\\\\\endcases ∂x∂f[i,j]≈f[i+1,j]−f[i,j]∂y∂f[i,j]≈f[i,j+1]−f[i,j]
因此图像边缘检测即是对图像的差分运算。
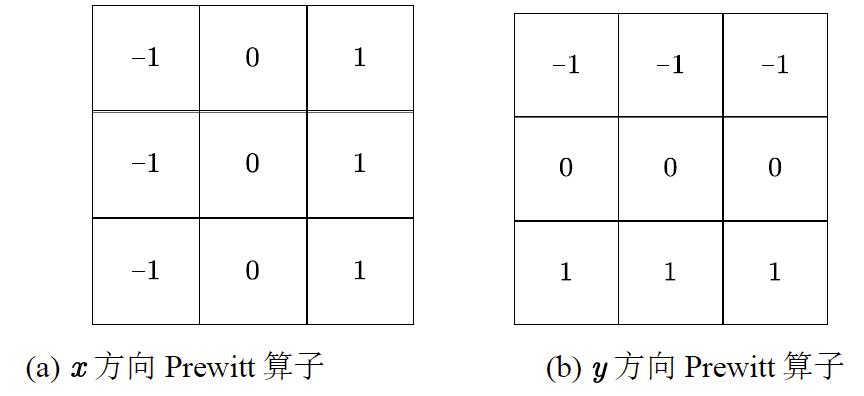
1.1 Prewitt算子
Prewitt算子本质上就是 x x x或 y y y方向上相邻像素的差分。
那我们常说的图像梯度是什么意思呢?
其实就是用 x x x与 y y y方向上相邻像素的差分为方向的向量
∇ f = [ ∂ f ∂ x ∂ f ∂ y ] \\nabla f=\\left[ \\beginmatrix \\frac\\partial f\\partial x& \\frac\\partial f\\partial y\\\\\\endmatrix \\right] ∇f=[∂x∂f∂y∂f]
在编程实现上,就是构造上图的两个方向的滤波算子,然后将 x x x、 y y y两个方向的边缘合成就是整张图各方向的边缘检测结果
def prewitt(self):
# Prewitt 算子
kernelX = np.array([[1,1,1],[0,0,0],[-1,-1,-1]], dtype=int)
kernelY = np.array([[-1,0,1],[-1,0,1],[-1,0,1]], dtype=int)
# 对图像滤波
x = cv2.filter2D(self.gray, cv2.CV_16S, kernelX)
y = cv2.filter2D(self.gray, cv2.CV_16S, kernelY)
# 转 uint8 ,图像融合
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
return cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

1.2 Sobel算子
对高斯核函数 x x x、 y y y方向求导,并将其模板化即得Sobel算子。Sobel算子相比于Prewitt算子有更强的抗噪能力,因为其结合了高斯滤波的效果。
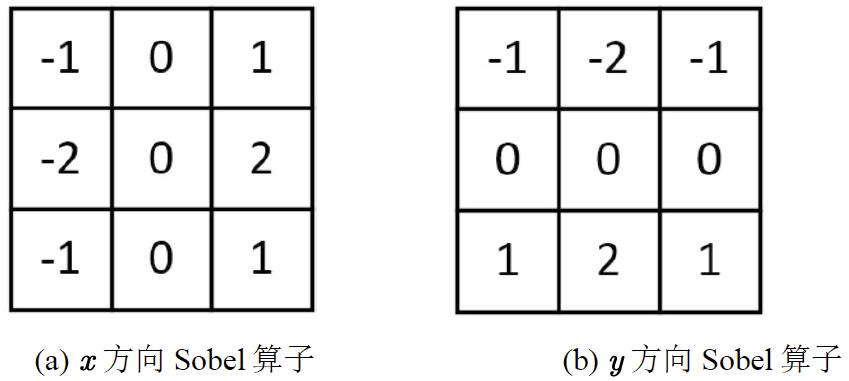
在编程实现上,就是构造上图的两个方向的滤波算子,然后将 x x x、 y y y两个方向的边缘合成就是整张图各方向的边缘检测结果
def sobel(self):
# Sobel 算子
kernelX = np.array([[1, 2, 1],[0, 0, 0],[-1, -2, -1]],dtype=int)
kernelY = np.array([[-1, -2, -1],[0, 0, 0],[1, 2, 1]],dtype=int)
# 对图像滤波
x = cv2.filter2D(self.gray, cv2.CV_16S, kernelX)
y = cv2.filter2D(self.gray, cv2.CV_16S, kernelY)
# 转 uint8 ,图像融合
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
return cv2.addWeighted(absX, 0.5, absY, 0.5, 0)

2 二阶微分算子
2.1 Laplace算子
将Laplace算子
∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 \\nabla ^2f=\\frac\\partial ^2f\\partial x^2+\\frac\\partial ^2f\\partial y^2 ∇2f=∂x2∂2f+∂y2∂2f
写成差分方程形式为
∇ 2 f = f ( x + 1 , y ) + f ( x − 1 , y ) + f ( x , y + 1 ) + f ( x , y − 1 ) − 4 f ( x , y ) \\nabla ^2f=f\\left( x+1,y \\right) +f\\left( x-1,y \\right) +f\\left( x,y+1 \\right) +f\\left( x,y-1 \\right) -4f\\left( x,y \\right) ∇2f=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)
将差分方程进一步写成卷积核形式如图(a),可将其扩展为图(b)使之具有各向同性。微分算子属于高通滤波,在锐化边缘的同时也增强了噪点,因此Laplace算子抗噪能力弱,且不能检测边缘方向。

在编程实现上,就是构造上图的滤波算子
# Laplace 算子
def laplace(self):
kernel = np.array([[0, -1, 0], [-1, 4, -1], [0, -1, 0]], dtype=int)
img = cv2.filter2D(self.gray, cv2.CV_16S, kernel)
return cv2.convertScaleAbs(img)

2.2 LoG算子
为克服Laplace算子抗噪能力弱这一问题,引入高斯-拉普拉斯算子(LoG, Laplace of Gaussian),即先低通滤除噪声,再高通强化边缘,LoG算子本质上是带通滤波器。
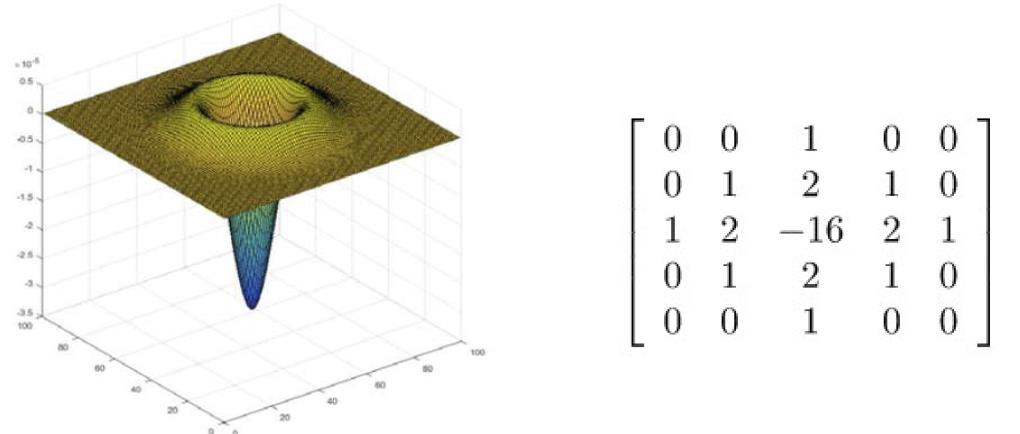
在编程实现上,就是构造上图的滤波算子
# LoG算子
def LoG(self):
kernel = np.array([[0, 0, 1, 0, 0], [0, 1, 2, 1, 0], [1, 2, -16, 2, 1], [0, 1, 2, 1, 0], [0, 0, 1, 0, 0]], dtype=int)
img = cv2.filter2D(self.gray, cv2.CV_16S, kernel)
return cv2.convertScaleAbs(img)

3 Canny边缘检测
Canny边缘检测算法可以分为以下步骤。
- 使用Sobel算子滤除原图像噪声,并得到梯度图;
- 应用非极大值抑制(Non-Maximum Suppression, NMS)以消除边缘检测、目标检测带来的杂散响应,即对待测边缘或目标,应尽可能有唯一的准确响应
- 应用双阈值(Double-Threshold)检测来确定真实的和潜在的边缘。
使用如下双阈值检测算法解决因噪声引起的杂散边缘响应。
i f G p ⩾ H i g h T h r e s h o l d : G p = S t r o n g E d g e e l s e i f G p ⩾ L o w T h r e s h o l d : G p = W e a k E d g e e l s e G p = S u p p r e s s e d E d g e if\\,\\,G_p\\geqslant HighThreshold: G_p=Strong\\,\\,Edge\\\\else\\,\\,if\\,\\,G_p\\geqslant LowThreshold: G_p=Weak\\,\\,Edge\\\\else\\,\\, G_p=Suppressed\\,\\,Edge ifGp⩾HighThreshold:Gp=StrongEdgeelseifGp⩾