OpenCV的cv2.minAreaRect解析

Posted 2023-04-08 求则得之，舍则失之

在这个文章中，我们将学习如何在感兴趣区域周围画最小面积矩形框。

1.最小面积矩形框

下图显示了两个矩形框，绿色的是普通矩形框，红色的是最小面积矩形框。可以发现，红色的是旋转矩形。

OpenCV提供了一个函数cv2.minAreaRect来寻找最小面积的旋转矩形。将2D点集作为输入，并返回一个Box2D结构，其中包括以下详细信息–（中心(x,y)，（宽度、高度）、旋转角度）。

(center(x,y), (width, height), angle of rotation) = cv2.minAreaRect(points)

但是要绘制一个矩形，我们需要矩形的四个角，因此为了将Box2D结构转换为4个角点，OpenCV提供了另一个函数cv2.boxPoints()，这将Box2D结构作为输入并返回4个角点。4个角点从y最高的点开始按顺时针顺序排列。语法如下：

points = cv2.boxPoints(box)

在绘制矩形之前，需要将4个角点转换为整数类型。可以使用np.int32或者np.int64（不要使用np.int8，因为它允许最大值127并截断）。有时，你可能会看到使用了np.int0，不要混淆，这相当于np.int32或者np.int64，具体取决于你的系统结构。完整的代码如下：

rect = CV2.minAreaRect(cnt)
box = cv2.boxPoints(rect)
box = np.int0(box)

得到四个坐标后，就可以轻松绘制图形了。现在，让我们讨论一下旋转角度。

2.旋转角度

获得四个角点以后，这四个角点从具有最高y的点开始按顺时针顺序排列，如下所示。如果2个点具有相同的最高y，则最右的点是起点。这些点被编号为0，1，2，3（0开始，3结束）。

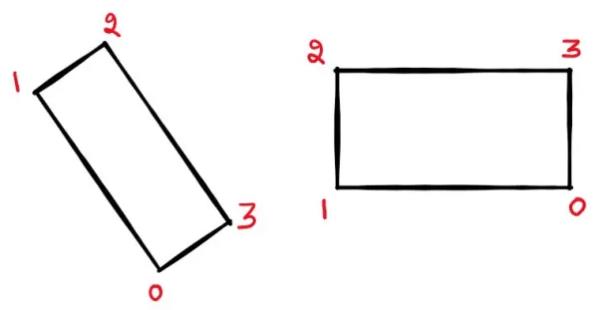
因此，OpenCV的cv2.minAreaRect()给出的旋转角度实际上是直线（连接起点和终点）与水平线之间的角度，如下所示。

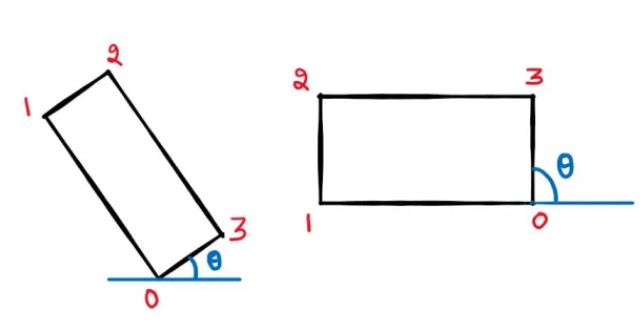
因此角度值始终位于[-90, 0)之间。为什么？因为如果对象旋转超过90°，则使用下一条边来计算与水平面的角度。因此计算出的角度始终位于[-90,0)之间。

实际角度是对象旋转的角度，计算出的角度是cv.minAreaRect()返回的角度。

参考目录

https://theailearner.com/tag/cv2-minarearect/

OpenCV源码解析

OpenCV K-means源码解析

OpenCV 图片读取源码解析

OpenCV 视频播放源码解析

OpenCV 追踪算法源码解析

OpenCV SIFT算法源码解析

OpenCV 滤波源码分析：bilareralFilter

OpenCV 数字识别解析

只捡需要的读

 

读懂OpenCV源码需要哪些基础？

通读过C++ Primer，目前C++属于入门级， 数字图像处理基础也有。目前看不懂OpenCV源码，请问还需要哪些基础， 从哪些方面入手源码比较好呢？谢谢

回答：

半年前实习的时候，在那个公司参与用OpenCV c++版本的开发公司自己的CV库。
体会还比较深，现在回想起来，大概会有这么一些建议：

1. C++需要多了解一下，建议看看Bjarne大神的书

OpenCV的C++版本是重新写过了的。
和以前的C版本是不同的了。
和图书馆里常见的那本learn OpenCV 已经不同了。

而对于C++来说，头文件里的interface和注释其实就是文档了。
如果单从一个学图像处理，和做实现的人来说，我觉得这就够了。

但是，即使要看头文件无障碍，也需要花很多功夫：
大约就是Bjarne的书里不断强调的 interface 和 implementation如何隔离。
而openCV c++ 里面还用到了很多 范型 (templates).
因为图像处理的应用对性能比较敏感，不可能像常见的应用一样，可以允许class之间复杂的继承关系，然后在运行的时候，再去查找virtual function table。
它们需要在编译的时候，就把这种搜索完成，于是需要 compile-time polymorphism。

2. 从 OpenCV 的文档开始

我觉得不要从源代码开始，而应该从官方的文档开始。
官方的文档介绍了很多它的设计思路，尤其是 C++版本的基本数据结构很重要。

3. 如果想要了解某个特征或者处理的具体实现，源代码不是最好的途径

我记得当时实习时要用到了某个特征。
实际上就原来来讲是非常简单的。
但是，当你真的去看源代码的时候，那就不容易了。
那是根据一片后来的文章实现的线性复杂度的算法。
我个人是属于算法与数据结构功底较差的，所以，当时看源代码对我来说反而更加吃了和无从下手。

实际上，网上的，尤其是国外的公开课教程是很棒的。

祝好。https://www.zhihu.com/question/28880447

https://www.xuebuyuan.com/3237438.html