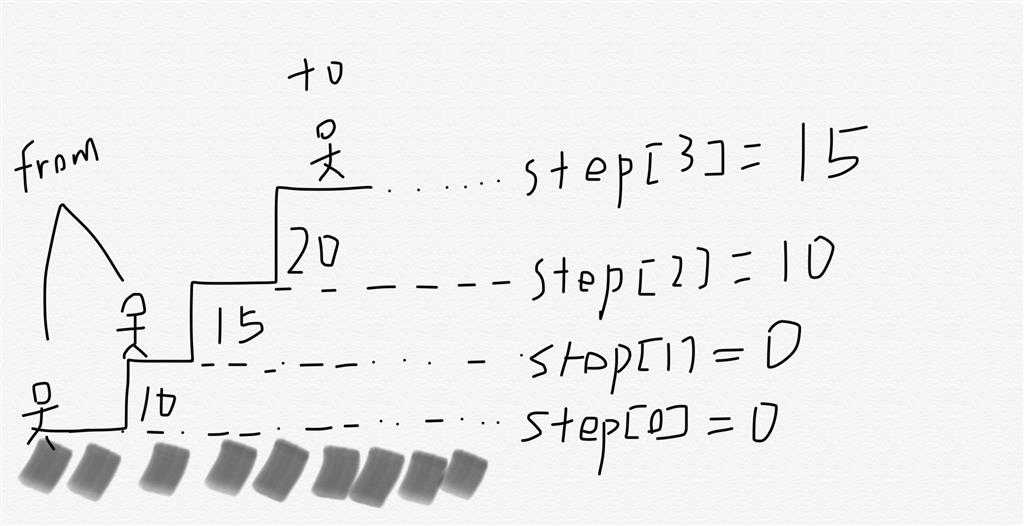Leetcode 746. Min Cost Climbing Stairs 最小成本爬楼梯 (动态规划)

Posted 2020-10-23 racaljk

题目翻译

有一个楼梯，第i阶用cost[i]（非负）表示成本。现在你需要支付这些成本，可以一次走两阶也可以走一阶。 问从地面或者第一阶出发，怎么走成本最小。

测试样例

Input: cost = [10, 15, 20]
Output: 15
Explanation: 从第一阶出发，一次走两步

Input: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
Output: 6
Explanation: 从地面出发，走两步，走两步，走两步，走一步，走两步，走一步。

详细分析

现在用step[i]表示走到第i阶的成本，要求step[i],我们只需在"到前一阶的成本+当前阶成本"和"到前两阶的成本+前两阶成本"取最小即可。一图胜千言：

 

因为step[0]和step[1]都可以作为开始出发地，所以成本都为0。注意一下爬两阶只需要那两阶的第一个成本作为总成本不需要两阶成本相加。所以

step[2] = min{step[1]+cost[1],step[0]+cost[0]} = min{10,15}=10

step[3] = min{step[2]+cost[2],step[1]+cost[1]} = min{30,15} = 15

代码实现

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        if(cost.size()==0){
            return 0;
        }
        if(cost.size()==1){
            return cost[0];
        }
        if(cost.size()==2){
            return std::min(cost[0],cost[1]);
        }
        int step[1024];
        step[0] = 0;
        step[1] = 0;
        for(int i=2;i<=cost.size();i++){
            step[i] = std::min(step[i-1]+cost[i-1],step[i-2]+cost[i-2]);
        }
        return step[cost.size()];
    }
};