day26 回溯算法的部分总结

Posted 2023-04-06 小生舞梦蝶

回溯算法的部分总结

回溯算法是一种常用于解决排列组合问题、搜索问题的算法，它的基本思想是将问题的解空间转化为一棵树，通过深度优先搜索的方式遍历树上的所有节点，找到符合条件的解。回溯算法通常使用递归实现，每次递归时传入当前搜索的状态和可能的选择，然后进行选择、回溯、取消选择等操作。下面是我对回溯算法的总结，希望能对你有所帮助。

1.回溯算法的基本框架
回溯算法的基本框架可以概括为以下几个步骤：

（1）判断是否到达终止条件，如果是则输出解并返回。

（2）遍历所有可能的选择，并进行选择。

（3）递归进入下一层，继续选择。

（4）回溯，撤销选择。

（5）循环步骤（2）-（4），直到遍历完所有可能的选择。

2.回溯算法的优化
回溯算法的时间复杂度通常比较高，因此需要进行一些优化，以提高算法效率。以下是一些常用的优化方法：

（1）剪枝：在搜索过程中，通过一些判断条件来排除不符合条件的状态，从而减少搜索的深度和宽度，提高搜索效率。

（2）选择优先级：将可能的选择按照某种优先级排序，优先搜索优先级高的选择，从而减少搜索深度。

（3）状态压缩：对于某些状态空间比较大的问题，可以使用状态压缩技巧来减少状态空间的大小，从而降低搜索的难度。

3.回溯算法的应用场景
回溯算法通常用于解决排列组合问题、搜索问题、优化问题等。以下是一些常见的应用场景：

（1）全排列问题：给定一个数组，求所有可能的排列。

（2）组合问题：给定一个数组和一个数k，求所有大小为k的组合。

（3）子集问题：给定一个数组，求所有可能的子集。

（4）图遍历问题：给定一个图，求从某个节点出发到达目标节点的所有路径。

（5）八皇后问题：在8*8的棋盘上，放置8个皇后，使得它们互相攻击不到。

回溯算法的一个总结

回溯算法的模板：

result = []

def backtrack(路径, 选择列表):

????if 满足结束条件:{

????????result.add(路径)

????????return

? ? }

?

? ? //每个for代表的其实就是一位，由这个for引出的下一个backtrack就是这位的下一位

????for 选择 in 选择列表:{

????????做选择

????????backtrack(路径, 选择列表)

????????撤销选择

? ? }

?

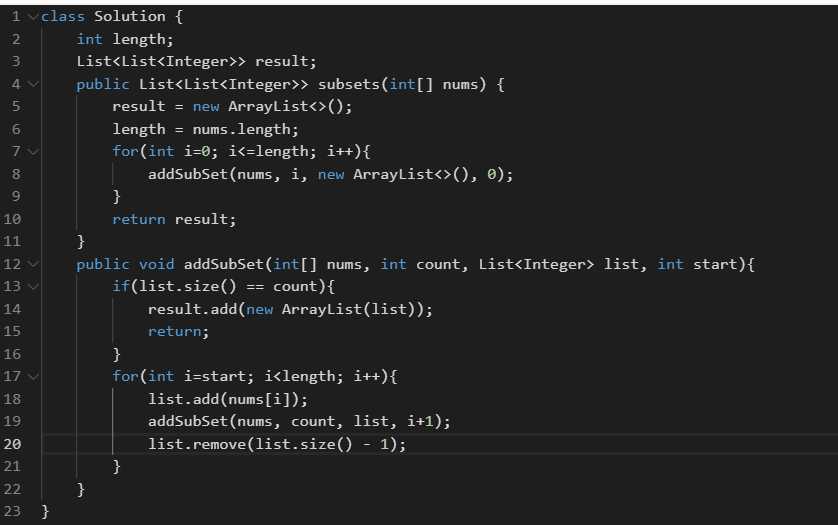
问题一：子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

?

?

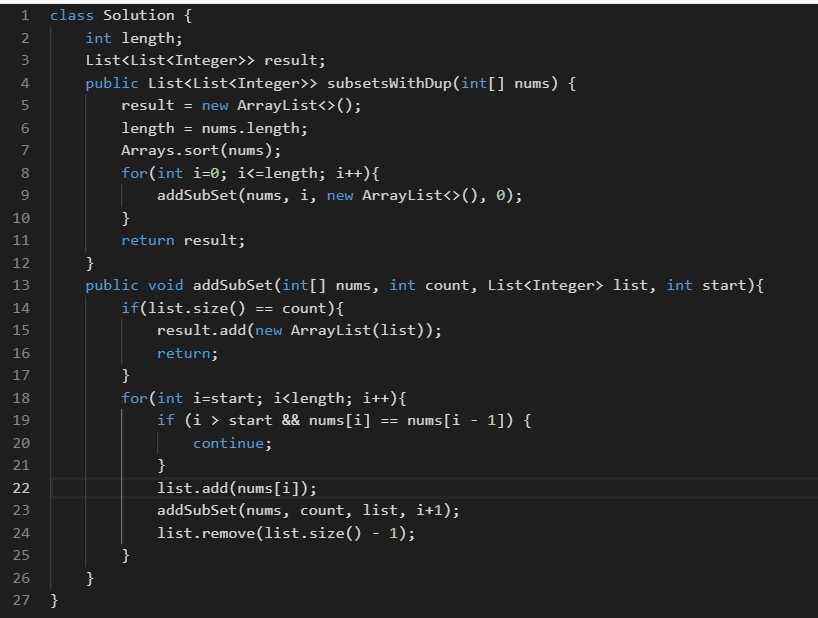
问题二：子集 II

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

?

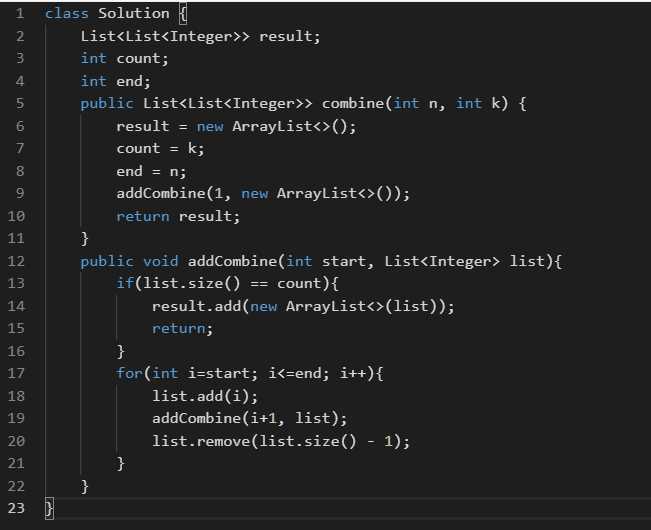
问题三：组合

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

?

?

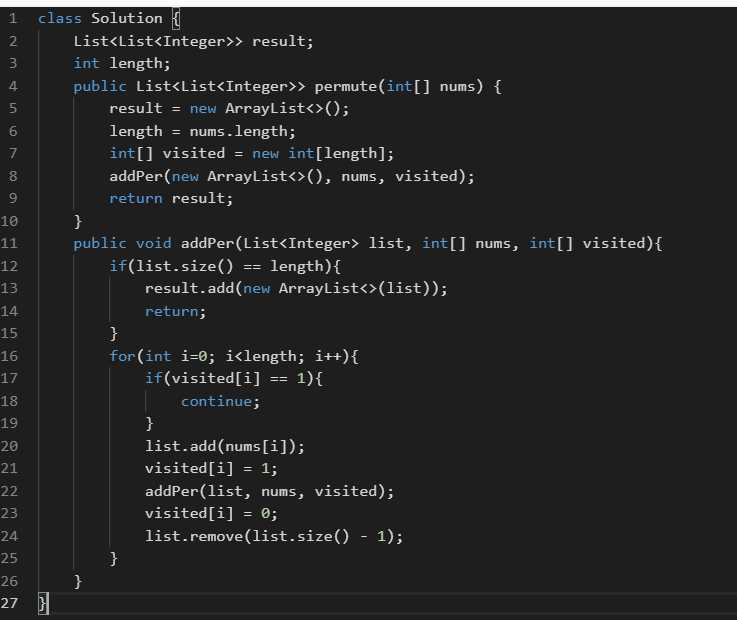
问题四：全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

?

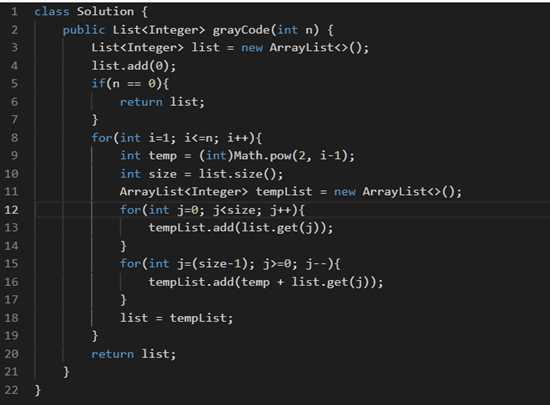
问题五：格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。即使有多个不同答案，你也只需要返回其中一种。

格雷编码序列必须以 0 开头。