3.1词典搜索的数据结构与通配符查询
Posted 心灵排骨汤
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了3.1词典搜索的数据结构与通配符查询相关的知识,希望对你有一定的参考价值。
提示:
词典及容错性检索(词典搜索的数据结构与通配符查询)
本节最重要的内容是:
(1)词典快速查找的数据结构
(2)非精确查询
(3)自动校正技术
希望大家学到:
(1)了解词典查找的数据结构
(2)理解通配符查询的思想
(3)掌握编辑距离的计算
(4)理解自动校正技术的思路
>>***其他内容(拼写校正)可转***<<
文章目录
词典搜索的数据结构
常用数据结构
哈希函数

二叉树
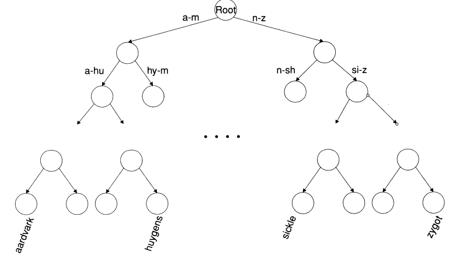
字典树
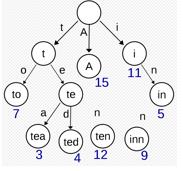
B树
内部节点可以多于两个
举例:2-3 B树只能有2-3个内部结点
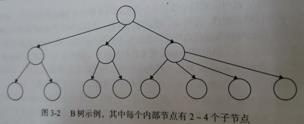
点击直达>>为什么平衡二叉树不适合索引:
索引是存在于索引文件中,是存在于磁盘中的。因为索引通常是很大的,因此无法一次将全部索引加载到内存当中,因此每次只能从磁盘中读取一个磁盘页的数据到内存中。而这个磁盘的读取的速度较内存中的读取速度而言是差了好几个级别。
注意,我们说的平衡二叉树结构,指的是逻辑结构上的平衡二叉树,其物理实现是数组。然后由于在逻辑结构上相近的节点在物理结构上可能会差很远。因此,每次读取的磁盘页的数据中有许多是用不上的。因此,查找过程中要进行许多次的磁盘读取操作。
而适合作为索引的结构应该是尽可能少的执行磁盘IO操作,因为执行磁盘IO操作非常的耗时。因此,平衡二叉树并不适合作为索引结构。
通配符查询

通配符查询:
| 方式 | 数据结构 | 举例 |
|---|---|---|
| 尾通配符查询 | B树 | mon* |
| 首通配符查询 | 反向B树 | *mon |
| 一般通配符查询 | B树和反向B树 | se*mon |
查询方法:
(1)轮排索引
在字符集中引入新的符号$,标识词项开始和结束。
举例:hello轮排索引部分
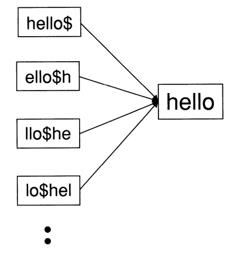

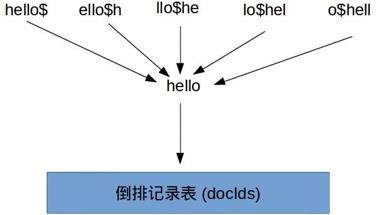

轮排索引特点:解决了通配符查询问题,结构简单,词典会非常大
(2)支持通配符查询的k-gram索引
k-gram代表由k个字符组成的序列。
举例:在词项castle中 cas、ast、tle都是3-gram。
如果用$字符标识词项开始和结束。那么该词项所有的3-gram有:$ca,cas,ast,stl,tle,le$。




倒排表数据结构通配符查询拼写纠正详解
目录:
- Dictionary Data Structure 词典数据结构
- Wild-Card Query 通配符查询
- Spelling Correction 拼写纠正
- 索引词(term vocabulary)。
- 文档频率(document frequency,即这个词在多少个文档里出现)。
- 指向倒排表的指针(pointers to each postings list )。
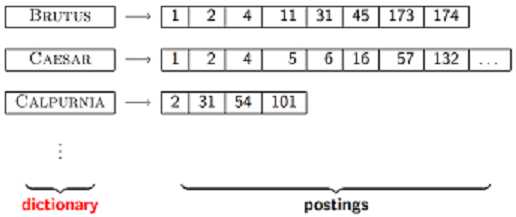


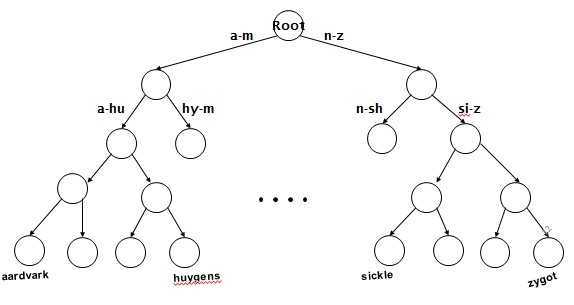
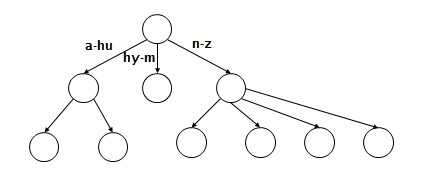
一棵m 阶的B-树满足下列特性的m 叉树:
- 树中每个结点至多有m 棵子树;
- 若根结点不是叶子结点,则至少有两棵子树;
- 除根结点之外的所有非终端结点至少有[m/2] 棵子树;
- 所有的非终端结点中包含以下信息数据:(n,A0,K1,A1,K2,…,Kn,An)。其中:Ki(i=1,2,…,n)为关键码,且Ki<Ki+1,Ai 为指向子树根结点的指针(i=0,1,…,n),且指针Ai-1 所指子树中所有结点的关键码均小于Ki (i=1,2,…,n),An 所指子树中所有结点的关键码均大于Kn。n为关键码的个数。
- 所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。
这样讲起来或许比较枯燥难懂,看这张图就好了:
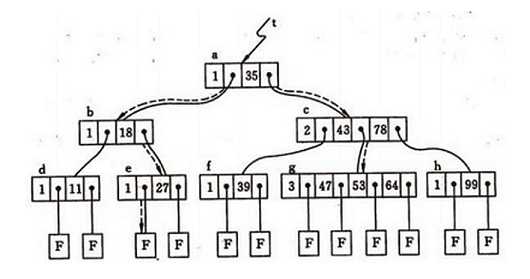
树的优点就是可以解决前缀查找的问题了。
缺点是速度比哈希慢点,是O(logM)并且要求是平衡的,重新平衡一棵树的代价大。(虽然B-树减轻了这种代价)
Wildcard queries,通配符查询。
比如查询语句 mon*:找出所有以mon开头的单词。如果采用树(或者B-树)结构词典,我们可以很容易的解决,只需要查询范围在mon ≤ w < moo的所有单词就ok了。
但是查询语句 *mon:找出所有以mon结尾的单词就比较困难了。其中一种办法就是我们增加一个额外的B-树来存储所有单词,以从后向前的顺序,然后在这个树上查询范围在nom ≤ w < non的所有单词。
可是如何处理通配符在单词中间的查询呢?
比如query是co*tion的话。我们当然可以分别在B-树查询到co*和*tion的所有单词然后合并这些单词,但是这样开销太大了。
解决办法就是:轮排索引(Permuterm Index),我们把query的通配符转换到结尾处。
设置一个标志$表示单词的结尾。
以hello举例,hello可以被转换成hello$, ello$h, llo$he, lo$hel, o$hell。$代表中hello的结束。现在,查询X等于查询X$,查询X*等于查询X*$,查询*X等于查询X$*,查询X*Y等于查询Y$X*。对于hel*o来说,X等于hel,Y等于o。
既然我们已经把通配符都弄到了单词尾部,现在我们又可以通过B-树像以前那样查询拉。
以上,我们已经完成了对query的转换,那么那些存储的索引的词要怎么处理才能配合这种query查询呢?
我们对索引来建立索引!!
Bigram indexes。就是两两个字母来索引。
举例来说,一个文本是“April is the cruelest month”,分别成Bigram indexes就是“$a,ap,pr,ri,il,l$,$i,is,s$,$t,th,he,e$,$c,cr,ru,ue,el,le,es,st,t$, $m,mo,on,nt,h$”,其中$ 代表着单词边界的符号。
那么如何对索引建立索引??
维护第二个倒排表,倒排表的索引词是Bigram indexes,posting list的值就是与之匹配的dictionary terms。
像这样:
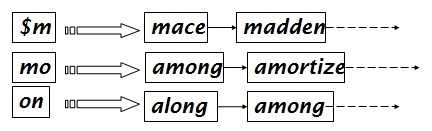
好了!目前为止,我们既对query进行了处理,也对terms进行了处理。
所以现在如果我们要查询 mon*,query会被分解成 $m AND mo AND on ,然后从上图中的倒排表做两个AND可以得到匹配的terms了!!
但是,我们会发现 $m AND mo AND on 也会匹配到单词moon,而moon不符合mon*的格式,这是他的一个缺点。我们必须要过滤掉这些词。
另外,一条查询语句往往相当多的布尔查询,这个开销也挺大的。
Spelling correction,拼写校正。
我们google一下 Alanis Morisett ,得到结果如图:
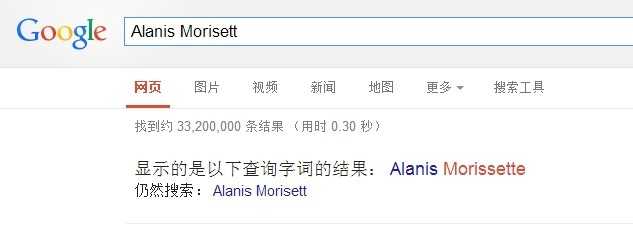
对了,就是这个提示,您找的是不是:xxxxxx。
在搜索引擎中,需要有一个可以查询到所有正确单词的词典。
给定一个词典和一个query,返回一个和query最接近的words。
怎么用才算是最接近??
- 编辑距离算法。
- 带权编辑距离算法。
编辑距离(Edit distance):
给定两个字符串S1和S2,从S1转换到S2的最小步骤就是他们的编辑距离。这些步骤包括,Insert(1步), Delete(1步), Replace(1步),copy(0步)。
比如说:
dof到dog的编辑距离是1,cat到act的编辑距离是2,cat到dog的编辑距离是3.
算法导论里关于编辑距离的伪代码如下:

举例子:算cats到fast的编辑距离~
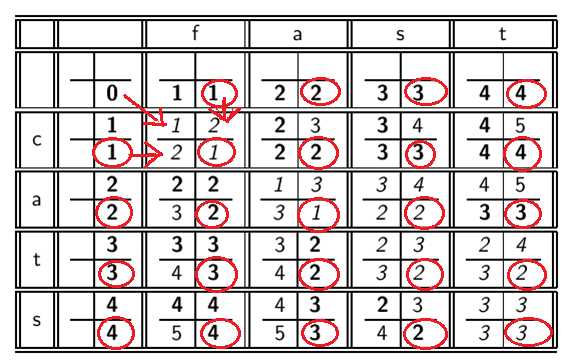
括号里圈出来的表示实际应该填的值,其他的只是用来进行对比,取其中最小的数。
具体到表中的每一格中四个数字的含义就是:
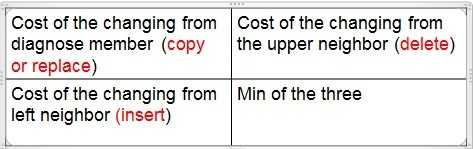
从左边的格子过来代表增加,上边的格子过来代表删除,斜上角的格子过来代表替换(此时两个字符不相等)或复制(此时两个字符不相等)。
编辑距离就是这样子。那么什么是带权编辑距离呢?
比如说,我们打字的时候,m被错打成n的几率会比m错打成p的几率更大,所以我们应该认为m和n的编辑距离小于m到p的编辑距离。因此将m替换为n时计算编辑距离应该比将m替换为p时的编辑距离小。
实现带权编辑距离,我们需要一个额外的权值矩阵。
那么,给定一个查询词,我们是不是得计算这个查询词和所有的索引词之间编辑距离呢?
答案是否定的,因为这样开销很大而且慢。
怎么用减少计算呢??
比如说,如果query是lord:
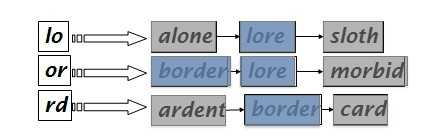
我们只取lo,or,rd中有重叠两次或以上的term,然后合并这些term,以这个为范围进行编辑距离的计算。
索引
其实在计算机中我们早已接触过跟索引有关的东西,比如数据库里的索引(index),还有硬盘文件系统中其实也有类似的东西,简而言之,索引是一种为了方便找到自己需要的东西而设计出来的条目,你可以通过找索引找到自己想要内容的位置。索引过程是: 关键字->索引->文档。在图书馆内的书分门别类,就是一种按类别来分的索引。当然索引还有很多其他的实现。
仅仅有索引的概念是不够的。虽然分门别类是一种方法,但是我们在拥有一堆文档的时候必须要有从文档到索引的规范过程,并且索引的结构要满足能够让人(或者计算机)快速找到的方法。面对一条长长的没有处理的索引列表,甚至还没有排好序,你可能要用O(N)的时间去看,头都大了。
为了满足这个要求,B+树,哈希表可以是比较好的选择,它们的复杂度分别是O(log N) 和 O(1)。
但是事实上为了满足特殊的要求,有些时候还要设计更加特殊的数据结构,比如后缀树组和trie树用来处理非文本的序列子串搜索。
在主要的搜索引擎中,还是靠文本搜索,而索引的设计其实并不固定,还要跟搜索策略结合,这些都是搜索引擎的部分。
倒排索引
倒排索引是索引的子集。在搜索引擎之中,正排索引跟倒排索引其实都有应用。
正排索引:知道文档d,得到d的关键字的位置序列,实现方式是 文档编号+关键字数组
倒排索引:知道关键字w,找到包含关键字的文档d1,d2,d3.... 实现方式是:关键字key做键的字典,值是文档编号数组
无论是哪一种索引,都要用一种能够快速检索的数据结构的来实现,否则它们都会面临大规模甚至超大规模的数据下无法工作的问题。
哈希表
哈希表,根据键找到值,复杂度为O(1)。它的实现是一组桶,每个桶=头部键+尾部链表。数据结构课程中对哈希表已经讲得很清楚了。它的问题在于空间消耗太大,而且可能会有哈希分配不平衡的问题。
跳表
参考一下 https://juejin.im/post/587c6cec61ff4b006501e006
跳表是一种特殊的链表,又称跳跃表,可以达到O(log N)的查询速度。这里的图说明了跳表的元素其实都在底层,但是可以有一些重复的层级为了方便检索。它的问题在于怎样平衡空间和时间效率上。
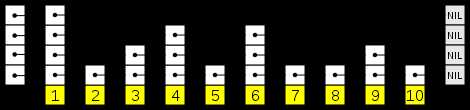
跳表中用到了概率,它设定某个跳表元素的i副本出现在i+1层的概率为p,根据概率对每个值求和得到元素k的期望出现次数 (∑p^k=1/(1-p), k = 1,2,...)。现实中并不会完全按照概率来进行设计,而是用一个固定的步长来设计多级的并联链表。
结论
倒排索引和跳表是为了方便检索和加快速度而设计的结构,并且在搜索引擎中为后续的其他操作提供了基础。现实中经常讲到的是倒排索引,以及跟它关联的tfidf。为了实现数据的快速搜索,还需要跟具体的数据结构相结合。
转载自:http://www.cnblogs.com/4everlove/p/3678414.html
以上是关于3.1词典搜索的数据结构与通配符查询的主要内容,如果未能解决你的问题,请参考以下文章