卷积神经网络(CNN)的整体框架及细节(详细简单)
Posted 小林学编程
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了卷积神经网络(CNN)的整体框架及细节(详细简单)相关的知识,希望对你有一定的参考价值。
一:引言
我们传统的神经网络和卷积神经网络有什么区别?
下图所示,左图就是我们传统的神经网络(NN)(想了解NN的小伙伴可以先划到最后的参考文章部分),右图就是卷积神经网络(Convolutional Neural Network)(CNN),我们在这张图中可以明显地看出,左图看上去像二维的,右图好像是一个三维的图,举个例子,比如在传统神经网络输入的一张图有784个像素点,所以输入层就有784个神经元,但在我们的CNN中输入的就是原始的图像28*28*1(是三维的),它是一个三维的矩阵。我们可以看到右图中又定义三维名称‘height*width*depth’简称‘h*w*d’,接下来我们就围绕着卷积层和深度到底怎么变换展开。
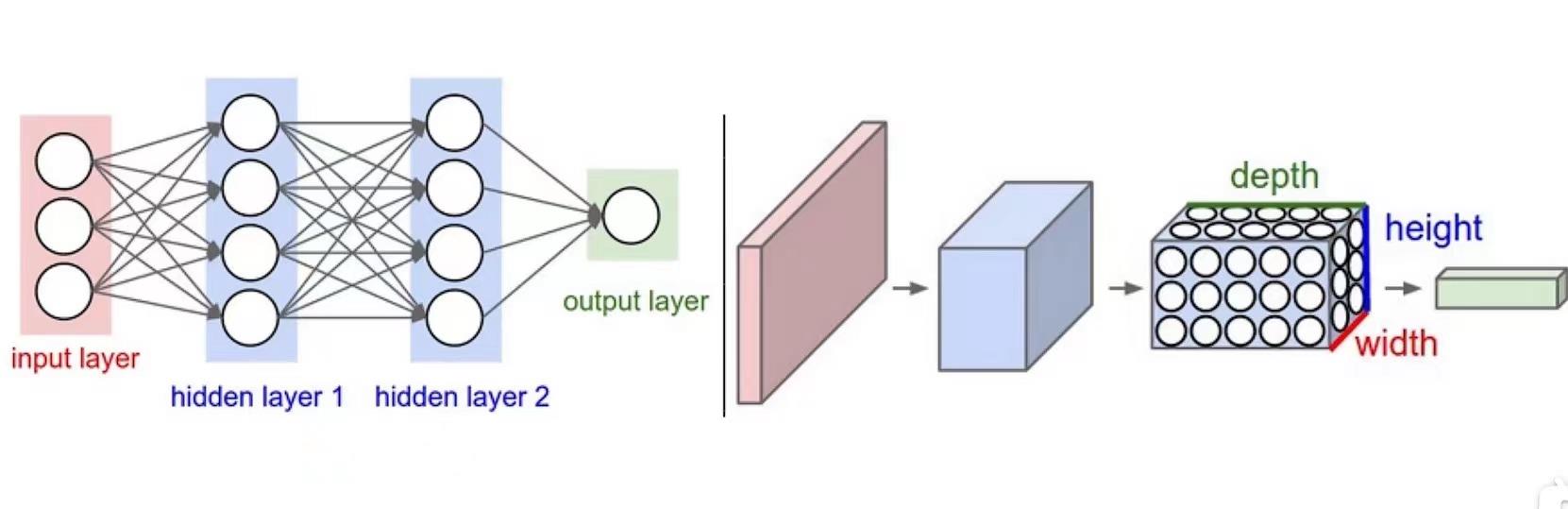
二:大体介绍CNN:
如下图所示就是CNN的整体架构,和我们讲述NN的文章相同,这次也是从整体架构入手,帮助大家了解CNN,总共有四个部分:输入层 ,卷积层 ,池化层 ,全连接层 。
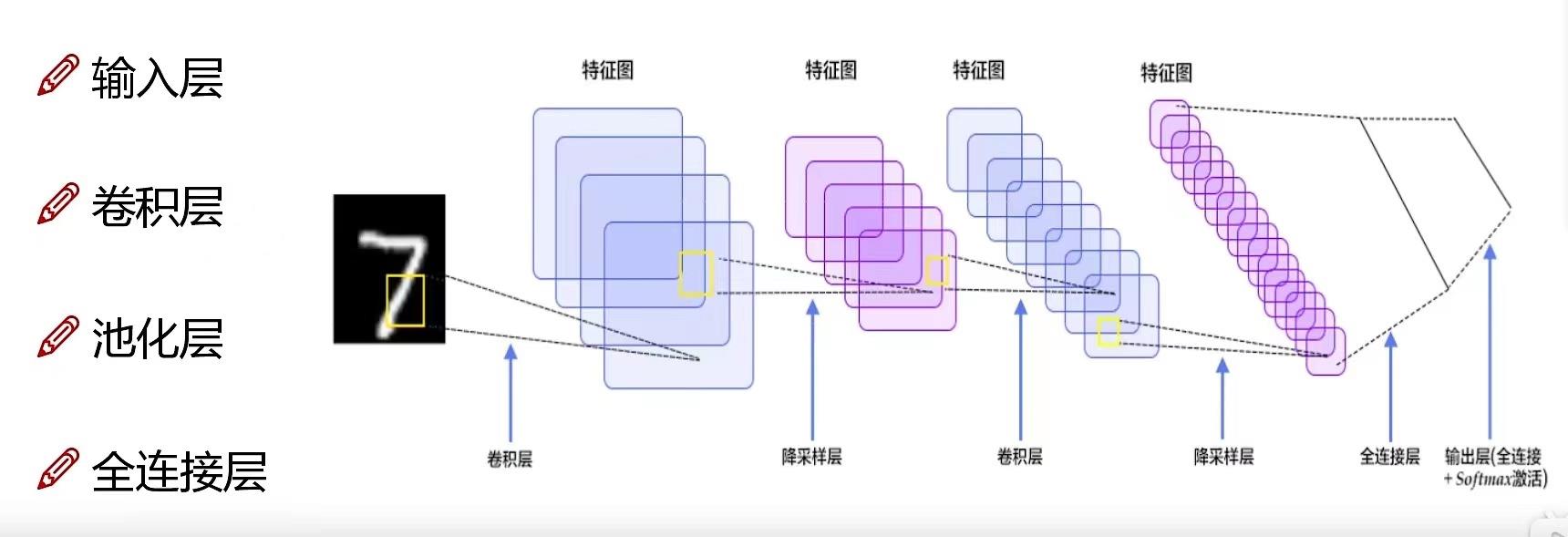
三:详细介绍CNN:
(1):输入层:
输入层就是和上文的例子相同,如图中的最左边的图片假设就是我们需要输入的,假设是‘28*28*3’,分别对应‘h*w*d’,其中对于图片输入来说通常是以RGB三通道的形式输入,所以d通常是3,如下图中的第二张图片就是后面三个通道图片相叠加而来
(2):卷积层(核心):
卷积层是如何工作的呢?我们先给定一个简单的例子,如下图所示:
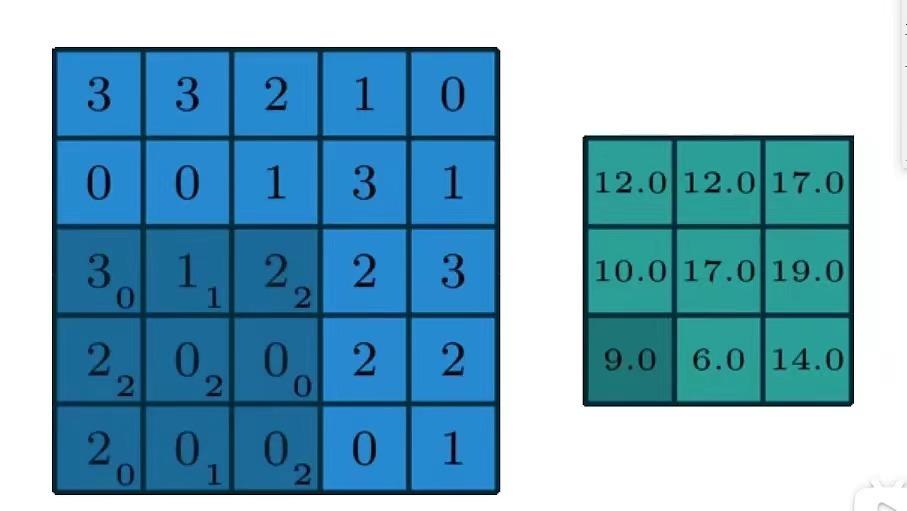
假设我们输入的是5*5*1的图像,中间的那个3*3*1是我们定义的一个卷积核(简单来说可以看做一个矩阵形式运算器),通过原始输入图像和卷积核做运算可以得到绿色部分的结果,怎么样的运算呢?实际很简单就是我们看左图中深色部分,处于中间的数字是图像的像素,处于右下角的数字是我们卷积核的数字,只要对应相乘再相加就可以得到结果。例如图中‘3*0+1*1+2*2+2*2+0*2+0*0+2*0+0*1+0*2=9’
那如果我们的d大于一的时候又是如何计算的?
如下动图:
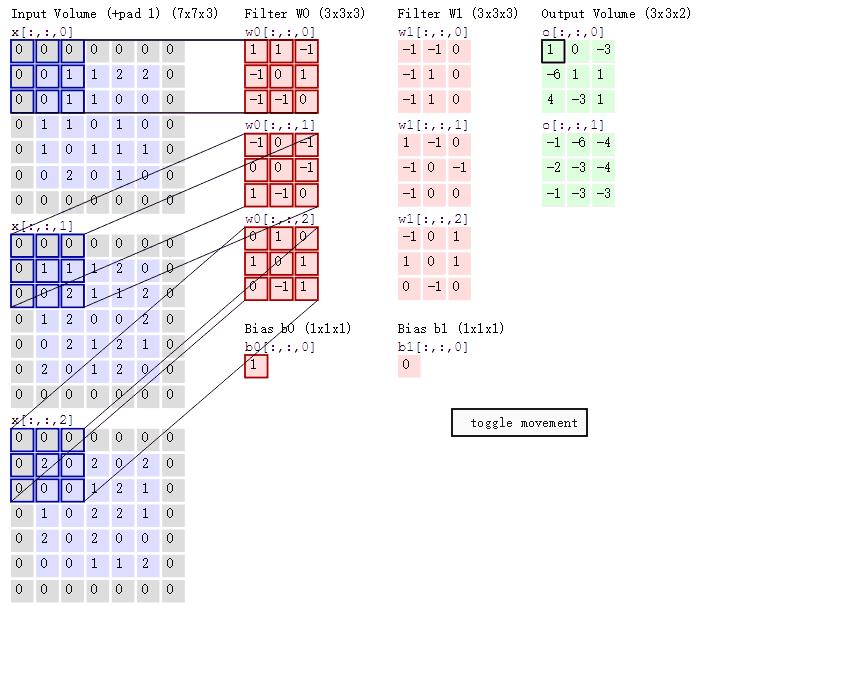
图中最左边的三个输入矩阵就是我们的相当于输入d=3时有三个通道图,每个通道图都有一个属于自己通道的卷积核,我们可以看到输出(output)的只有两个特征图意味着我们设置的输出的d=2,有几个输出通道就有几层卷积核(比如图中就有FilterW0和FilterW1),这意味着我们的卷积核数量就是输入d的个数乘以输出d的个数(图中就是2*3=6个),其中每一层通道图的计算与上文中提到的一层计算相同,再把每一个通道输出的输出再加起来就是绿色的输出数字啦!。
(3):池化层:
池化层部分就比较简单了如下图所示:
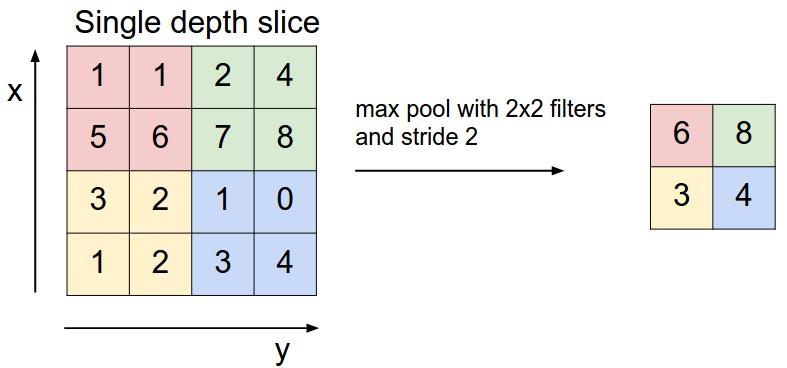
如图中就是一个max-pooling(最大池化)的一个操作,就是把选中的区域中的最大值给挑出来,比如粉红色区域的‘1,1,5,6’四个数字最大值就是6,还有一种比较常见的是mean-pooling(平均池化)就是把区域内的数字加起来做个平均值,比如蓝色区域就是(1+0+3+4)/4=2。
(4):全连接层(FC)
全连接层的理解就是相当于在最后面加一层或多层传统神经网络(NN)层,我们在连接全连接层前,需要把我们的CNN的三维矩阵进行展平成二维,比如说从池化层出来的是‘5*5*3’的图像,在输入到全连接层展平成1*75以满足全连接层的输入模式。
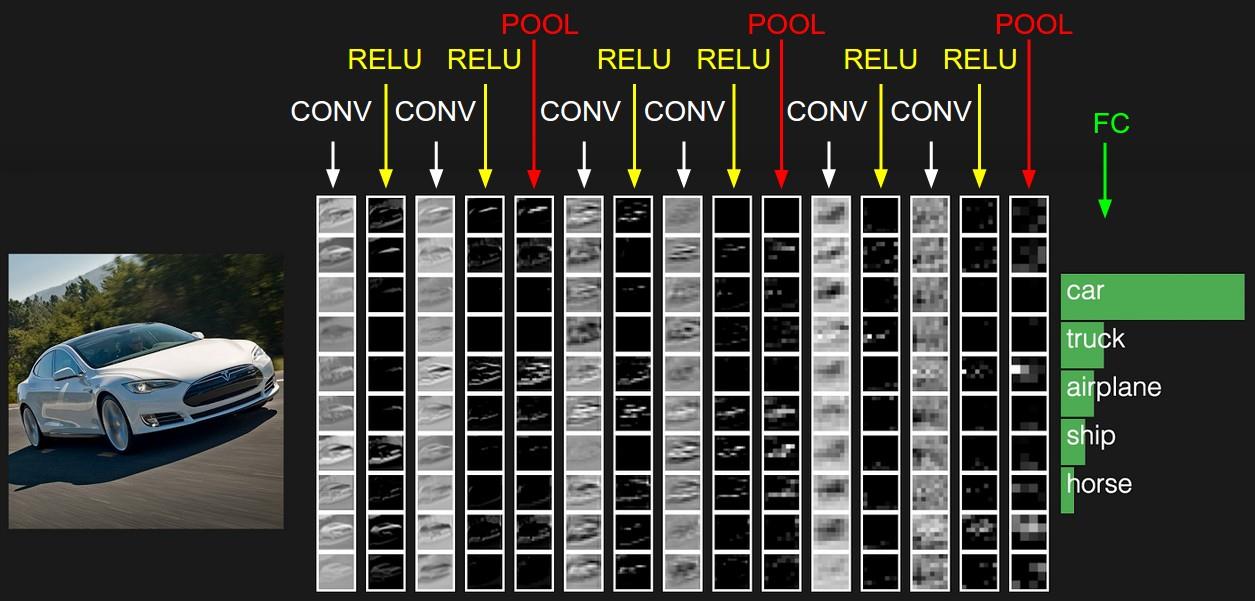
四:最后呈现
如下图:
五:参考文章:
1:CNN笔记:通俗理解卷积神经网络_v_JULY_v的博客-CSDN博客_卷积神经网络通俗理解
2:CNN部分不愧是计算机博士唐宇迪居然半天教会了我大学4年没学会的深度学习经典算法解析入门到实战课程,看不懂你打我!!!_哔哩哔哩_bilibili
3:传统神经网络:
神经网络整体架构及细节(详细简单)_小林学编程的博客-CSDN博客
卷积神经网络(CNN)讲解及代码
相关文章:
1. 经典反向传播算法公式详细推导
2. 卷积神经网络(CNN)反向传播算法公式详细推导
网上有很多关于CNN的教程讲解,在这里我们抛开长篇大论,只针对代码来谈。本文用的是matlab编写的deeplearning toolbox,包括NN、CNN、DBN、SAE、CAE。在这里我们感谢作者编写了这样一个简单易懂,适用于新手学习的代码。由于本文直接针对代码,这就要求读者有一定的CNN基础,可以参考Lecun的Gradient-Based Learning Applied to Document Recognition和tornadomeet的博文
首先把Toolbox下载下来,解压缩到某位置。然后打开Matlab,把文件夹内的util和data利用Set Path添加至路径中。接着打开tests文件夹的test_example_CNN.m。最后在文件夹CNN中运行该代码。
下面是test_example_CNN.m中的代码及注释,比较简单。
load mnist_uint8; %读取数据
% 把图像的灰度值变成0~1,因为本代码采用的是sigmoid激活函数
train_x = double(reshape(train_x',28,28,60000))/255;
test_x = double(reshape(test_x',28,28,10000))/255;
train_y = double(train_y');
test_y = double(test_y');
%% 卷积网络的结构为 6c-2s-12c-2s
% 1 epoch 会运行大约200s, 错误率大约为11%。而 100 epochs 的错误率大约为1.2%。
rand('state',0) %指定状态使每次运行产生的随机结果相同
cnn.layers =
struct('type', 'i') % 输入层
struct('type', 'c', 'outputmaps', 6, 'kernelsize', 5) % 卷积层
struct('type', 's', 'scale', 2) % pooling层
struct('type', 'c', 'outputmaps', 12, 'kernelsize', 5) % 卷积层
struct('type', 's', 'scale', 2) % pooling层
;
opts.alpha = 1; % 梯度下降的步长
opts.batchsize = 50; % 每次批处理50张图
opts.numepochs = 1; % 所有图片循环处理一次
cnn = cnnsetup(cnn, train_x, train_y); % 初始化CNN
cnn = cnntrain(cnn, train_x, train_y, opts); % 训练CNN
[er, bad] = cnntest(cnn, test_x, test_y); % 测试CNN
%plot mean squared error
figure; plot(cnn.rL);
assert(er<0.12, 'Too big error');下面是cnnsetup.m中的代码及注释。
function net = cnnsetup(net, x, y)
assert(~isOctave() || compare_versions(OCTAVE_VERSION, '3.8.0', '>='), ['Octave 3.8.0 or greater is required for CNNs as there is a bug in convolution in previous versions. See http://savannah.gnu.org/bugs/?39314. Your version is ' myOctaveVersion]); %判断版本
inputmaps = 1; % 由于网络的输入为1张特征图,因此inputmaps为1
mapsize = size(squeeze(x(:, :, 1))); %squeeze():除去x中为1的维度,即得到28*28
for l = 1 : numel(net.layers) % 网络层数
if strcmp(net.layersl.type, 's') % 如果是pooling层
mapsize = mapsize / net.layersl.scale; % pooling之后图的大小
assert(all(floor(mapsize)==mapsize), ['Layer ' num2str(l) ' size must be integer. Actual: ' num2str(mapsize)]);
for j = 1 : inputmaps
net.layersl.bj = 0; % 偏置项
end
end
if strcmp(net.layersl.type, 'c') % 如果是卷积层
mapsize = mapsize - net.layersl.kernelsize + 1; % 确定卷积之后图像大小
fan_out = net.layersl.outputmaps * net.layersl.kernelsize ^ 2; % 上一层连到该层的权值参数总个数
for j = 1 : net.layersl.outputmaps % 第l层特征图的数量
fan_in = inputmaps * net.layersl.kernelsize ^ 2; % 上一层连到该层的第j个特征图的权值参数
for i = 1 : inputmaps % 上一层特征图的数量
net.layersl.kij = (rand(net.layersl.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out)); % 初始化权值,见论文Understanding the difficulty of training deep feedforward neural networks
end
net.layersl.bj = 0; % 偏置项
end
inputmaps = net.layersl.outputmaps; % 用该层的outputmaps更新inputmaps的值并为下一层所用
end
end
% 'onum' is the number of labels, that's why it is calculated using size(y, 1). If you have 20 labels so the output of the network will be 20 neurons.
% 'fvnum' is the number of output neurons at the last layer, the layer just before the output layer.
% 'ffb' is the biases of the output neurons.
% 'ffW' is the weights between the last layer and the output neurons. Note that the last layer is fully connected to the output layer, that's why the size of the weights is (onum * fvnum)
fvnum = prod(mapsize) * inputmaps; % 最终输出层前一层的结点数目
onum = size(y, 1); % 类别数目
% 最后一层全连接网络的参数
net.ffb = zeros(onum, 1);
net.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));
end
下面是cnntrain.m中的代码及注释。
function net = cnntrain(net, x, y, opts)
m = size(x, 3);
numbatches = m / opts.batchsize;
if rem(numbatches, 1) ~= 0
error('numbatches not integer');
end
net.rL = [];
for i = 1 : opts.numepochs
disp(['epoch ' num2str(i) '/' num2str(opts.numepochs)]);
tic; %tic和toc配套使用来求运行时间
kk = randperm(m);
for l = 1 : numbatches
batch_x = x(:, :, kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));
batch_y = y(:, kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));
net = cnnff(net, batch_x); % 前向传播
net = cnnbp(net, batch_y); % BP反向传播
net = cnnapplygrads(net, opts);
if isempty(net.rL)
net.rL(1) = net.L;
end
net.rL(end + 1) = 0.99 * net.rL(end) + 0.01 * net.L;
end
toc;
end
end下面是cnnff.m中的代码及注释。
function net = cnnff(net, x)
n = numel(net.layers);
net.layers1.a1 = x;
inputmaps = 1;
for l = 2 : n % 除输入层以外的每一层
if strcmp(net.layersl.type, 'c') % 卷积层
% !!below can probably be handled by insane matrix operations
for j = 1 : net.layersl.outputmaps % 该层的每一个特征图
% 该层的输出:上一层图片大小-kernel+1
z = zeros(size(net.layersl - 1.a1) - [net.layersl.kernelsize - 1 net.layersl.kernelsize - 1 0]);
for i = 1 : inputmaps % 对于每一个输入特征图(本例中为全连接)
% 每个特征图的卷积都相加,convn()为matlab自带卷积函数
z = z + convn(net.layersl - 1.ai, net.layersl.kij, 'valid');
end
% 加入偏置项,并通过sigmoid函数(现今一般采用RELU)
net.layersl.aj = sigm(z + net.layersl.bj);
end
% 用该层的outputmaps更新inputmaps的值并为下一层所用
inputmaps = net.layersl.outputmaps;
elseif strcmp(net.layersl.type, 's')
% mean-pooling
for j = 1 : inputmaps
z = convn(net.layersl - 1.aj, ones(net.layersl.scale) / (net.layersl.scale ^ 2), 'valid'); % !! replace with variable
% 取出有效的mean-pooling矩阵,即每隔net.layersl.scale提取一个值
net.layersl.aj = z(1 : net.layersl.scale : end, 1 : net.layersl.scale : end, :);
end
end
end
% 把最后一层展开变成一行向量方便操作
net.fv = [];
for j = 1 : numel(net.layersn.a)
sa = size(net.layersn.aj);
net.fv = [net.fv; reshape(net.layersn.aj, sa(1) * sa(2), sa(3))];
end
% 加上权值和偏置项并通入sigmoid(多类别神经网络的输出一般采用softmax形式,损失函数使用cross entropy )
net.o = sigm(net.ffW * net.fv + repmat(net.ffb, 1, size(net.fv, 2)));
end
下面是cnnbp.m中的代码及注释,比较复杂。首先要有普通BP的基础,可以参考CeleryChen的博客,而CNN的反向传播略有不同,可以参考tornadomeet的博客。
function net = cnnbp(net, y)
n = numel(net.layers);
net.e = net.o - y; % 误差
% loss函数,这里采用的方法是MSE(多类别神经网络的输出一般采用softmax形式,损失函数使用cross entropy)
net.L = 1/2* sum(net.e(:) .^ 2) / size(net.e, 2);
%% backprop deltas
net.od = net.e .* (net.o .* (1 - net.o)); % 输出层delta,包括sigmoid求导(delta为loss函数对该层未经激活函数结点的导数)
net.fvd = (net.ffW' * net.od); % 隐藏层(倒数第二层)delta
if strcmp(net.layersn.type, 'c') % 只有卷积层才可以通过sigmoid函数,本CNN结构最后一个隐藏层为pooling
net.fvd = net.fvd .* (net.fv .* (1 - net.fv));
end
% 把最后一隐藏层的delta向量变成形如a的向量
sa = size(net.layersn.a1);
fvnum = sa(1) * sa(2);
for j = 1 : numel(net.layersn.a)
net.layersn.dj = reshape(net.fvd(((j - 1) * fvnum + 1) : j * fvnum, :), sa(1), sa(2), sa(3));
end
% 逆向传播,计算各层的delta
for l = (n - 1) : -1 : 1
if strcmp(net.layersl.type, 'c') % 卷积层且下一层为pooling层
for j = 1 : numel(net.layersl.a) % 对该层每一个特征图操作(考虑sigmoid函数,upsample)
net.layersl.dj = net.layersl.aj .* (1 - net.layersl.aj) .* (expand(net.layersl + 1.dj, [net.layersl + 1.scale net.layersl + 1.scale 1]) / net.layersl + 1.scale ^ 2);
end
elseif strcmp(net.layersl.type, 's') % pooling层且下一层为卷积层
for i = 1 : numel(net.layersl.a)
z = zeros(size(net.layersl.a1));
for j = 1 : numel(net.layersl + 1.a) % 第l+1层所有特征核的贡献之和
X = net.layersl + 1.kij;
z = z + convn(net.layersl + 1.dj, flipdim(flipdim(X, 1), 2), 'full');
%z = z + convn(net.layersl + 1.dj, rot180(net.layersl + 1.kij), 'full');
end
net.layersl.di = z;
end
end
end
%% 通过delta计算梯度
for l = 2 : n
if strcmp(net.layersl.type, 'c') % 只有卷积层计算梯度,pooling层的参数固定不变
for j = 1 : numel(net.layersl.a)
for i = 1 : numel(net.layersl - 1.a)
net.layersl.dkij = convn(flipall(net.layersl - 1.ai), net.layersl.dj, 'valid') / size(net.layersl.dj, 3); % 旋转180°,卷积,再旋转180°
end
net.layersl.dbj = sum(net.layersl.dj(:)) / size(net.layersl.dj, 3); % 所有delta相加,除以每一次批处理的个数
end
end
end
net.dffW = net.od * (net.fv') / size(net.od, 2); %除以每次批处理个数
net.dffb = mean(net.od, 2);
function X = rot180(X)
X = flipdim(flipdim(X, 1), 2);
end
end下面是cnnapplygrads.m中的代码,比较简单,在这里就不进行注释了。
function net = cnnapplygrads(net, opts)
for l = 2 : numel(net.layers)
if strcmp(net.layersl.type, 'c')
for j = 1 : numel(net.layersl.a)
for ii = 1 : numel(net.layersl - 1.a)
net.layersl.kiij = net.layersl.kiij - opts.alpha * net.layersl.dkiij;
end
net.layersl.bj = net.layersl.bj - opts.alpha * net.layersl.dbj;
end
end
end
net.ffW = net.ffW - opts.alpha * net.dffW;
net.ffb = net.ffb - opts.alpha * net.dffb;
end
以上是关于卷积神经网络(CNN)的整体框架及细节(详细简单)的主要内容,如果未能解决你的问题,请参考以下文章