二梯度下降算法

Posted 2023-04-05 beyond谚语

课后作业

以前喜欢用微软自带的paint绘图，总感觉少些什么，现在直接手推，感觉效果会更好些，虽然字体很丑，但印象更深。

梯度下降算法(Gradient Descent Algorithm)推导

无非就是求导呗，推导如下，以y=w*x线性函数为例哈

y = w * x函数拟合（梯度下降法）

import matplotlib.pyplot as plt

# 定义数据集  假设函数为y = 3 * x
x_data = [1.,2.,3.,4.,5.]
y_data = [3.,6.,9.,12.,15.]
epoch_list = [] #保存下训练次数
cost_list = []  #保存下每次训练的MSE损失值

# 初始化w，假设为1
w = 1.

def forward(x): #预测值，即y_hat
    return x * w

def cost(xs,ys): #MSE损失函数
    loss_all = 0
    for x,y in zip(xs,ys):
        y_hat = forward(x) #拿到模型预测值y_hat
        loss_all += (y_hat - y) ** 2 #将每个loss求和得到loss_all
    return loss_all / len(xs) #这里为了求平均值，len(xs)和len(ys)都可以

def gradient(xs,ys): #梯度
    grad = 0
    for x,y in zip(xs,ys):
        grad += 2 * x * (w * x - y)
    return grad / len(ys)

print("Predict:",4,"\\ny_real:",forward(4)) #因为w初始值设置的是1，故模型输出4.0


for epoch in range(500): #训练500个epoch
    cost_val = cost(x_data,y_data) #拿到MSE损失函数值
    grad_val = gradient(x_data,y_data) #拿到当前位置的梯度
    w -= 0.001 * grad_val #更新w参数
    print("Epoch:",epoch,"\\tw=",w,"\\tloss=",cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)
print("Predict:",4,"\\ny_real:",forward(4)) #此时的w通过梯度下降法更新w，可以得到很接近真确答案的值   

#绘图，方便看出训练效果
plt.plot(epoch_list,cost_list)
plt.ylabel('MSE Value')
plt.xlabel('Epoch')
plt.show()

梯度下降法类似贪心算法，本质思想都是求得局部最优解
不一定是全局最优解，但一定是局部最优解

然而，梯度下降法最主要的弊端，就是鞍点问题不容易解决。鞍点处导数为
，w无法再继续更新了，嘎住了。

为了解决鞍点问题，随机梯度下降法出现了，主要区别在于：
梯度下降法的损失函数值是全部样本的平均值
随机梯度下降的损失函数是随机抽取单个样本
正因为这一点，随机抽取单个样本，可以使得w一点一点挪动

梯度下降法虽然性能不高，惧怕鞍点，但它可以并行训练，因为直接没有必然的联系；
随机梯度下降法根据随机抽取的单一样本计算梯度可以很好的避免鞍点的出现，但因为每个w的更新都需要上一个w的介入，故不可以并行训练。

y = w * x函数拟合（随机梯度下降法）

import matplotlib.pyplot as plt

# 定义数据集  假设函数为y = 3 * x
x_data = [1.,2.,3.,4.,5.]
y_data = [3.,6.,9.,12.,15.]
epoch_list = [] #保存下训练次数
cost_list = []  #保存下每次训练的MSE损失值

# 初始化w，假设为1
w = 1.

def forward(x): #预测值，即y_hat
    return x * w

def loss(xs,ys): #MSE损失函数
    y_hat = forward(x) #拿到模型预测值y_hat
    loss_all = (y_hat - y) ** 2 #随机抽取一个loss作为最终的loss_all
    return loss_all

def gradient(x,y): #单一样本的梯度
    grad = 2 * x * (w * x - y)
    return grad

print("Predict:",4,"\\ny_real:",forward(4)) #因为w初始值设置的是1，故模型输出4.0


for epoch in range(500): #训练500个epoch
    for x,y in zip(x_data,y_data):
        grad_val = gradient(x,y) #拿到当前位置的梯度
        w -= 0.001 * grad_val #更新w参数
        l = loss(x,y)
        print("Epoch:",epoch,"\\tw=",w,"\\tloss=",l)
    epoch_list.append(epoch)
    cost_list.append(l)

print("Predict:",4,"\\ny_real:",forward(4)) #此时的w通过随机梯度下降法更新w，可以得到很接近真确答案的值   

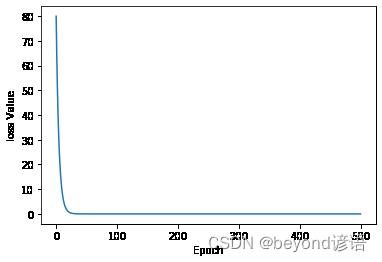
#绘图，方便看出训练效果
plt.plot(epoch_list,cost_list)
plt.ylabel('loss Value')
plt.xlabel('Epoch')
plt.show()

总结：
梯度下降法
①求所有样本的loss，求和得到cost，再取平均值
②求所有样本的梯度
③更新w

随机梯度下降法
①取所有样本中的一个，求梯度
②更新w
③求单个样本的loss

PyTorch学习2B站刘二大人《PyTorch深度学习实践》——梯度下降算法（Gradient Descent）

b站课程链接：梯度下降算法

一、梯度下降算法
1.简介
梯度下降算法是一种求解函数最优值的迭代算法，给定一个初值，通过负梯度方向进行更新查找。
2.程序实现及结果

import matplotlib.pyplot as plt

# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 初始化权重
w = 1.0

# 定义线性拟合函数
def forward(x):
    return x * w

# 定义损失函数（均方误差）
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

# 定义梯度函数
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

# 存储迭代次数和损失函数
epoch_list = []
cost_list = []

print('predict (before training)：','x = 4','y=',forward(4)) #训练之前：预测

# 梯度下降算法
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= 0.05 * grad_val  # 0.01 learning rate
    print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
    epoch_list.append(epoch)
    cost_list.append(cost_val)

print('predict (after training)：','x = 4','y =',forward(4)) #训练之后：预测

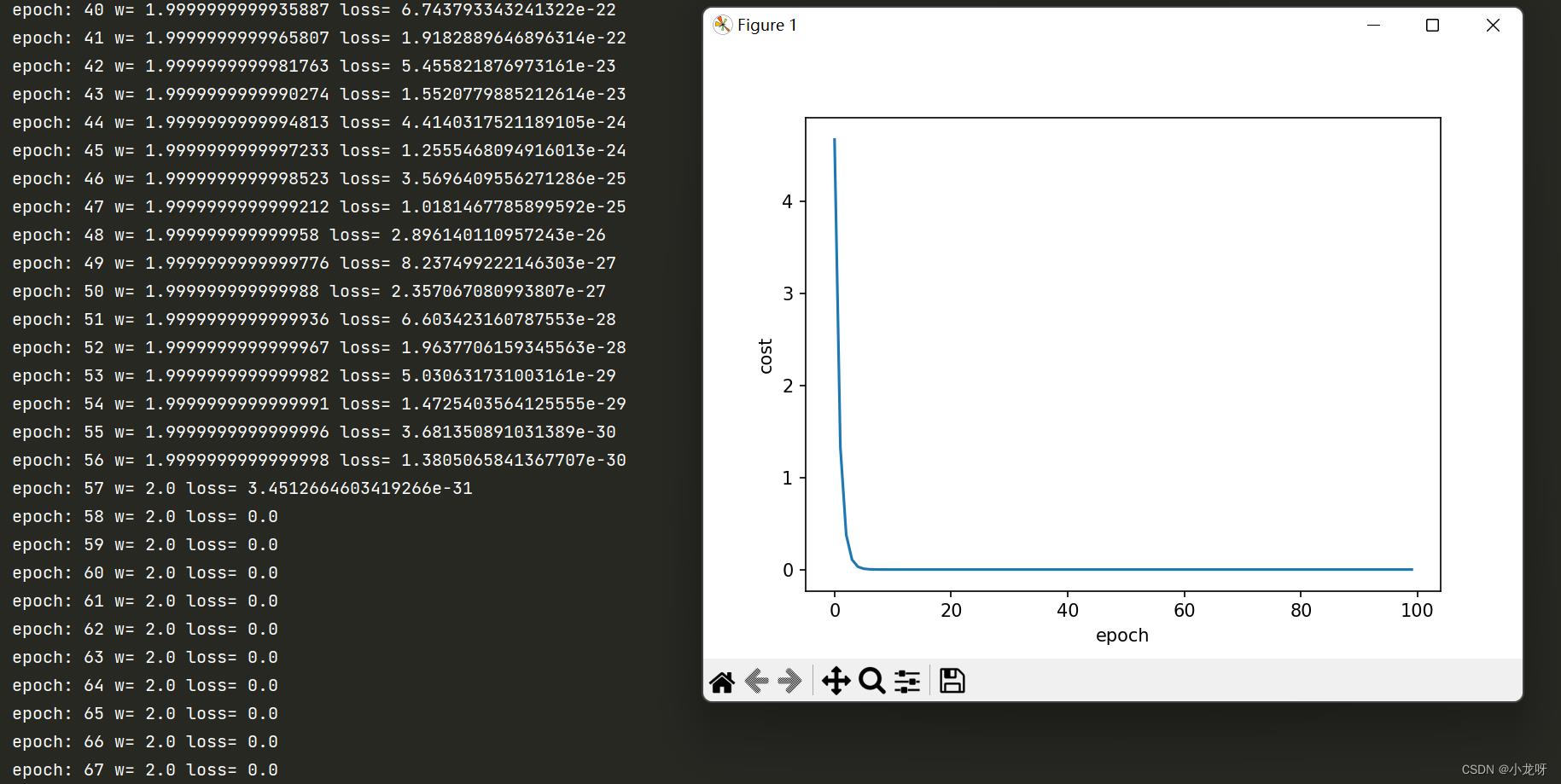
# 可视化
plt.plot(epoch_list, cost_list)
plt.ylabel('cost')
plt.xlabel('epoch')
plt.show()

二、随机梯度下降算法
1.简介

• 由于在最优解计算中，梯度下降算法往往会陷入局部最优的情况，所以我们引进随机梯度下降算法。在每一次迭代中，我们使用每一个训练样本的梯度进行参数更新。
• 这样可以使我们达到一个全局最优的情况，但是相应的计算复杂度也会提高，不太适用于训练样本较多的情况。在深度学习中，我们可以通过小批量随机梯度下降(Mini-Batch SGD)加速训练。

2.程序实现及结果

import matplotlib.pyplot as plt

# 训练集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 初始化权重
w = 1.0

# 定义线性拟合函数
def forward(x):
    return x * w

# 定义损失函数
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

# 定义梯度函数
def gradient(x, y):
    return 2 * x * (x * w - y)

# 存储迭代次数和损失函数
epoch_list = []
loss_list = []

print('predict (before training)：','x = 4','y=',forward(4)) #训练之前：预测

# 随机梯度下降算法（stochastic gradient descent）
# 每个epoch都使用三个样本分别进行参数更新，一共更新100*3=300次
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        grad = gradient(x, y)
        w = w - 0.05 * grad  # 通过训练集中每个样本的梯度进行参数更新
        print("\\t grad:", x, y, grad)
        l = loss(x, y)
    print("progress:", epoch, "w=", w, "loss=", l)
    epoch_list.append(epoch)
    loss_list.append(l)

print('predict (after training)：','x = 4','y =',forward(4)) #训练之后：预测

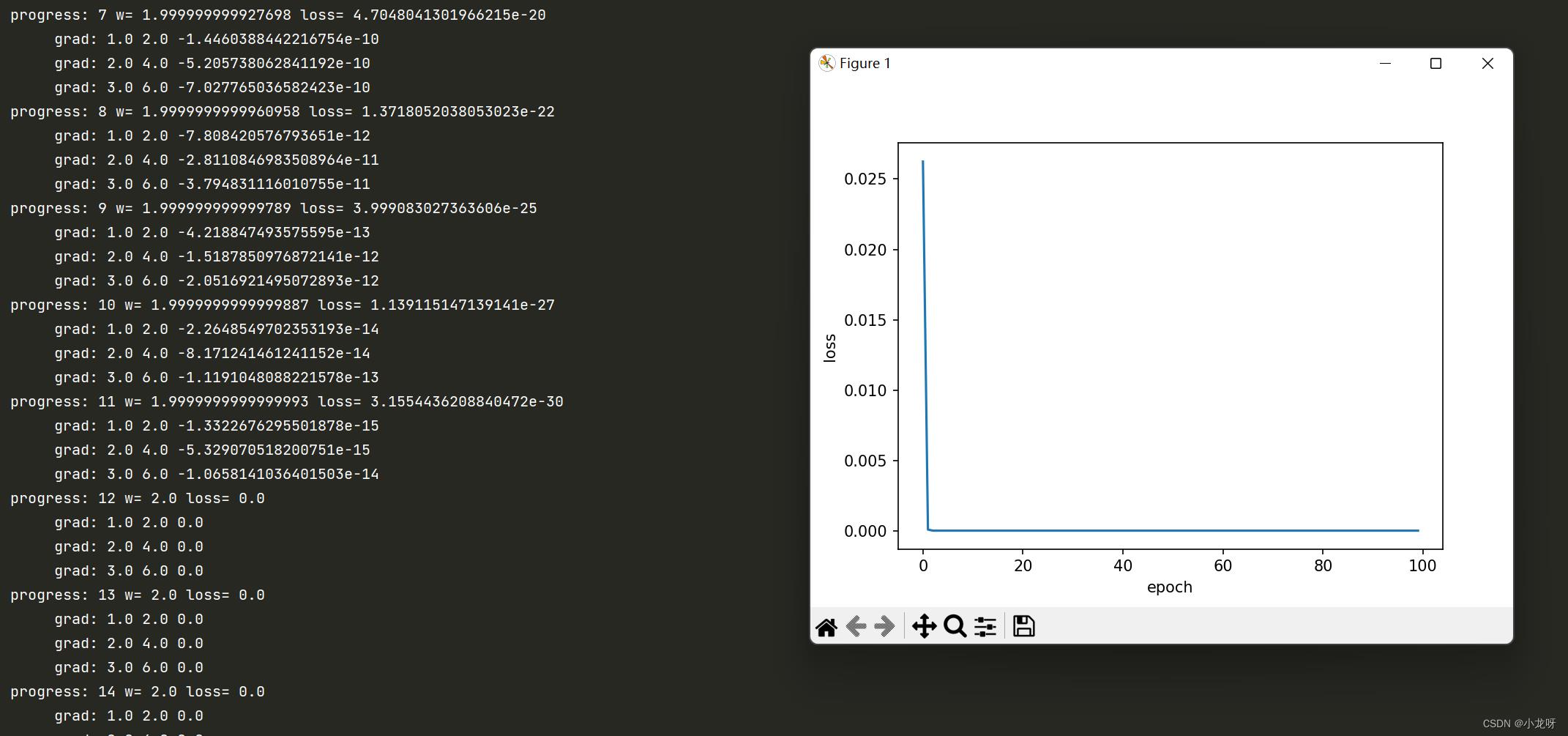
# 可视化
plt.plot(epoch_list, loss_list)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()