深度学习中的学习率设置技巧与实现详解

Posted Chaos_Wang_

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深度学习中的学习率设置技巧与实现详解相关的知识，希望对你有一定的参考价值。

❤️觉得内容不错的话，欢迎点赞收藏加关注😊😊😊，后续会继续输入更多优质内容❤️

👉有问题欢迎大家加关注私戳或者评论（包括但不限于NLP算法相关，linux学习相关，读研读博相关......）👈

（封面图由文心一格生成）

深度学习中的学习率设置技巧与实现详解

深度学习中的学习率是一个非常重要的超参数，对模型的训练和结果影响极大。在深度学习模型中，学习率决定了参数更新的步长，因此合理设置学习率对于优化算法的收敛速度、模型的训练效果以及泛化性能都有很大的影响。本文将介绍深度学习中的学习率设置技巧，包括常用的学习率衰减方法、自适应学习率方法以及学习率预热等。

1. 常用的学习率衰减方法

1.1 学习率衰减

学习率衰减是一种常见的优化算法，它可以随着训练的进行，逐渐减小学习率，从而使得模型在训练初期能够快速地收敛，而在训练后期能够更加稳定地更新参数。学习率衰减的方法有很多种，包括Step Decay、Exponential Decay、Polynomial Decay等。

Step Decay是一种常见的学习率衰减方法，它是在训练的过程中，根据固定的步数对学习率进行逐步地降低。例如，假设初始学习率为0.1，每隔10个epoch将学习率降低10倍，那么当训练到第11个epoch时，学习率将变为0.01，当训练到第21个epoch时，学习率将变为0.001，以此类推。这种方法简单易行，但是需要手动设置衰减的步数和衰减的幅度，不太灵活。

Exponential Decay是一种常见的指数衰减方法，它可以根据训练的epoch数来逐渐减小学习率。具体而言，Exponential Decay方法的学习率衰减规则如下：

α = α 0 ⋅ e − k t \\alpha=\\alpha_0 · e^-kt α=α0​⋅e−kt

其中， α 0 \\alpha_0 α0​表示初始学习率， k k k为衰减系数， t t t表示训练的epoch数。随着训练的进行， t t t会不断增大，因此学习率会不断减小。Exponential Decay方法可以通过设置不同的 k k k值来控制学习率的衰减速度，从而达到更好的训练效果。

Polynomial Decay是一种常见的多项式衰减方法，它可以通过多项式函数来逐渐减小学习率。具体而言，Polynomial Decay方法的学习率衰减规则如下：
α = α ⋅ ( 1 − t T ) p \\alpha=\\alpha\\cdot (1 - \\fractT)^p α=α⋅(1−Tt​)p
其中， α 0 \\alpha_0 α0​表示初始学习率， p p p为多项式的幂次数， t t t表示训练的epoch数， T T T为总的训练epoch数。随着训练的进行， t t t会不断增大，因此学习率会不断减小，同时随着 p p p的增大，学习率的衰减速度也会加快。

1.2 余弦退火

余弦退火（Cosine Annealing）是一种新兴的学习率衰减方法，它通过余弦函数来逐渐减小学习率，从而达到更好的训练效果。具体而言，余弦退火方法的学习率衰减规则如下：
α = α 0 ⋅ 1 + cos ⁡ ( π ⋅ t T ) 2 \\alpha = \\alpha_0 \\cdot \\frac1 + \\cos(\\frac\\pi \\cdot tT)2 α=α0​⋅21+cos(Tπ⋅t​)​

其中， α 0 \\alpha_0 α0​表示初始学习率， t t t表示训练的epoch数， T T T为总的训练epoch数。随着训练的进行， t t t会不断增大，因此学习率会不断减小，同时余弦函数的周期也会不断缩小，从而使得学习率在训练过程中逐渐降低。

1.3 One Cycle Learning Rate

One Cycle Learning Rate是一种比较新的学习率衰减方法，它通过在训练初期使用一个较大的学习率，从而快速地收敛到一个局部最优解，然后在训练后期使用一个较小的学习率，从而逐步地优化模型。具体而言，One Cycle Learning Rate方法的学习率变化规则如下：

  • 在训练初期，使用较大的学习率（如初始学习率的10倍），从而快速地收敛到一个局部最优解；
  • 然后在训练中期，使用较小的学习率，从而逐步地优化模型；
  • 最后在训练后期，再次使用较小的学习率，从而让模型更加稳定。
    One Cycle Learning Rate方法可以有效地提高模型的训练速度和泛化性能，但是需要仔细调整超参数，否则容易导致模型的过拟合。

2. 自适应学习率方法

除了学习率衰减方法之外，深度学习中还有很多自适应学习率方法，包括Adagrad、Adadelta、Adam等。这些方法都是基于梯度信息来自适应地调整学习率，从而在训练过程中更加稳定和高效。

2.1 Adagrad

Adagrad是一种自适应学习率方法，它可以根据参数梯度的大小来动态地调整学习率。具体而言，Adagrad方法的学习率更新规则如下：

其中， α 0 \\alpha_0 α0​表示初始学习率， g i g_i gi​表示参数的梯度， ϵ \\epsilon ϵ是一个非常小的常数，用于防止分母为0。Adagrad方法的优点在于它可以根据参数的梯度大小自适应地调整学习率，从而更好地适应不同的数据分布和参数更新。但是Adagrad方法也有一些缺点，比如需要存储梯度平方和的累积值，导致内存占用较大；另外，由于学习率是逐渐减小的，因此可能会导致模型在后期训练时收敛速度变慢。

2.2 Adadelta

Adadelta是一种自适应学习率方法，它可以根据参数梯度的大小和历史梯度信息来动态地调整学习率Adadelta方法的优点在于它可以动态地调整学习率，并且不需要存储梯度平方和的累积值，因此内存占用较小。但是Adadelta方法也有一些缺点，比如需要手动设置一些超参数，例如平均梯度的衰减率和初始的平均梯度值等。

2.3 Adam

Adam是一种自适应学习率方法，它可以根据参数梯度的大小和历史梯度信息来动态地调整学习率，并且还可以适应不同的数据分布和参数更新。具体而言，Adam方法的学习率更新规则如下：
m t = β 1 ⋅ m t − 1 + ( 1 − β 1 ) ⋅ g t v t = β 2 ⋅ v t − 1 + ( 1 − β 2 ) ⋅ g t 2 m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t Δ x t = − α v ^ t + ϵ ⋅ m ^ t \\beginalignedm_t &= \\beta_1 \\cdot m_t-1 + (1 - \\beta_1) \\cdot g_t \\\\ v_t &= \\beta_2 \\cdot v_t-1 + (1 - \\beta_2) \\cdot g_t^2 \\\\ \\hatm_t &= \\fracm_t1 - \\beta_1^t \\\\ \\hatv_t &= \\fracv_t1 - \\beta_2^t \\\\ \\Delta x_t &= -\\frac\\alpha\\sqrt\\hatv_t+\\epsilon \\cdot \\hatm_t\\endaligned mt​vt​m^t​v^t​Δxt​​=β1​⋅mt−1​+(1−β1​)⋅gt​=β2​⋅vt−1​+(1−β2​)⋅gt2​=1−β1t​mt​​=1−β2t​vt​​=−v^t​ ​+ϵα​⋅m^t​​

其中， g t g_t gt​表示参数的梯度， m t m_t mt​和 v t v_t vt​分别表示梯度的一阶和二阶矩， β 1 \\beta_1 β1​和 β 2 \\beta_2 β2​是衰减率， m ^ t \\hatm_t m^t​和 v ^ t \\hatv_t v^t​分别表示修正后的一阶和二阶矩， α \\alpha α表示初始学习率， ϵ \\epsilon ϵ是一个非常小的常数，用于防止分母为0。
Adam方法的优点在于它不仅可以动态地调整学习率，还可以适应不同的数据分布和参数更新，从而在训练过程中更加稳定和高效。但是Adam方法也有一些缺点，比如需要手动设置一些超参数，例如衰减率和初始学习率等。
三、学习率预热
学习率预热是一种常见的训练技巧，它可以在训练初期使用一个较小的学习率，从而避免模型在训练初期过度更新参数，导致模型不稳定。具体而言，学习率预热的方法是在训练前先使用一个较小的学习率进行一些预热操作，例如在训练初期进行一些预热的epoch，然后再逐步地增加学习率，从而使得模型更加稳定和高效。
学习率预热的方法可以有效地避免模型在训练初期过度更新参数，导致模型不稳定，同时也可以加速模型的收敛速度，提高训练效率和泛化性能。

3. 代码实现

下面是使用PyTorch实现常见的学习率衰减方法和自适应学习率方法的代码示例：

3.1 Step Decay

import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.1
一文详解深度学习中的Normalization




一、 深度学习中的 Internal Covariate Shift（ICS）


深度学习的训练过程可以看成很多层的叠加，而每一层的参数更新会导致下一层输入数据的分布发生变化，通过层层累加，高层的输入分布变化会非常剧烈导致上层的数据需要不断去变化以适应底层参数的更新。因此学习率，初始化权重等超参数的设置对模型的收敛非常重要，从而导致训练困难。总结下来，每个神经元的输入数据不再是独立同分布的，这样会造成：


    

  1. 

    上层参数需要不断适应新的输入数据分布，降低学习速度
    

    2. 

  2. 

    下层输入的变化可能趋向于变大或者变小，导致上层落入饱和区，使学习过早停止
    

    3. 

  3. 

    每层的更新都会影响到其他层
    

    4. 



这种现象被称为深度学习中的 (Internal Covariate Shift, ICS) 。因此，在数据喂给机器学习模型之前，需要进行白化处理，去除特征之间的相关且保证所有的特征具有相同的均值和方差。


二、Normalization 的通用框架


以一个神经元为例，接收一组输入向量 \\(x = (x_{1},x_{2},...x_{n})\\)，输出一个标量 \\(y\\)，即：


\\[y = f(x)
\\]
由于ICS问题的存在，输入向量  \\(x\\) 的元素之间的差别极大，因此需要对每一层的输入数据都进行白化，保证 \\(x\\) 之间独立同分布。然而标准的白化操作代价很大。因此随着Google在2015年首先提出的Batch Normalization操作，很多Normalization操作也都被设计出来。基本思想是在将 \\(x\\) 送给神经元之前，先做平移和伸缩变换，将其分布规范在固定区间的标准分布：


\\[h = f(g\\times \\dfrac{x-u}{\\sigma}+b)
\\]
首先将输入向量 \\(x\\) 归一化为 \\((0，1)\\) 的标准分布，讲道理来说这一步已经做了白化操作，然而为了保证模型的表达能力不因为规范化而下降，继续通过再缩放参数  \\(g\\) 和再平移参数 \\(b\\) 进一步得到符合 \\((b, g^{2})\\) 的分布。因为如果不进行再平移和再缩放，无论下层神经元学到了什么，在输入上层神经元之前都被调整为这一固定范围。因此定义可学习参数 \\((b, g^{2})\\) 来保证网络 的学习能力。


那么通过先白化再变换之后，引入了两个新参数 \\((b, g^{2})\\) ，导致新的输入向量的均值只跟可学习的参数有关，从而去除了与下层计算的相关性。


三、主流的Normalization框架








    

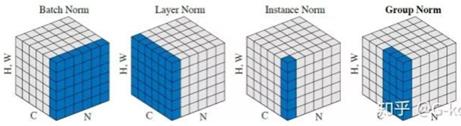
  1. Batch Norm是在 batch 上对 \\([B, H, W]\\) 做归一化，而保留通道 \\(C\\) 的维度。可以看成一共 \\(B\\) 张图，每张图有 \\(C\\) 个通道，每个通道有 \\([H, W]\\) 个像素，因此BN的均值和方差可以看成第1张图的第1个通道上所有像素与第2张图的第1个通道的所有像素相加，除以像素总数 \\(2\\times H \\times W\\) 就得到了均值 \\(u \\in R^{1\\times C \\times 1 \\times 1}\\)，即不同图片对应的相同通道上所有像素全部加起来，再除以像素总数 \\(B\\times H \\times W\\)。BN 独立地规范所有batch size的不同维度的所有数据，这就要求每一个batch之间以及batch与整体数据之间应该是近似同分布的，如果分布差距较大，那么不同batch的数据将会进行不一样的数据变化，同样增加了模型训练的难度。因此BN适用于每个mini-batch比较大，数据比较接近的场景，如CNN。然而而Batch Size过大又会占用过多的显存，一种折中的办法就是梯度累积来实现大Batch Size 的效果。
    2. 

  2. Layer Norm针对 BN 不适用深度固定不变的网络的问题，在通道方向上，对 \\([C, H, W]\\) 做归一化，相当于把每张图片的所有像素加起来，再除以该图片的像素总数 \\(C\\times H \\times W\\)，得到的均值 \\(u \\in R^{B \\times 1 \\times1 \\times 1}\\)，主要适用于 RNN。
    3. 

  3. Instance Norm在图像像素上对 H, W做归一化，相当于把每个通道的所有像素加起来，再除以该通道的像素综述 H*W, 得到的均值 \\(u \\in R^{B \\times C \\times1 \\times 1}\\)，主要用在图像的风格迁移。因为在图像风格化中，生成结果主要依赖于某个图像实例，feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格。所以对整个batch归一化不适合图像风格化中，因而对H、W做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。
    4. 

  4. Group Norm相当于将通道进行分组，对每一组的数据进行 Layer Norm。为了解决BN对较小的mini-batch size效果差的问题。GN 适用于占用显存比较大的任务，例如图像分割。对这类任务，可能 batch size 只能是个位数，再大显存就不够用了。而当 batch size 是个位数时，BN 的表现很差，因为没办法通过几个样本的数据量，来近似总体的均值和标准差。就像在显存不够的情况下，计算n个mini batch的梯度值后再进行梯度更新，实现小batch size更准确的梯度值。
    5. 



四、Normalization 有效性的分析


    

  1. 权重伸缩不变性：当权重 \\(W\\) 按照常量 \\(\\lambda\\) 进行伸缩时，得到的规范化后的值保持不变，即：
    2. 



\\[Norm(\\lambda Wx) = Norm(g\\dfrac{\\lambda WX-\\lambda u}{\\lambda \\sigma}+b) = Norm(Wx)
\\]
因此权重伸缩变化对反向传播没有影响。


2）数据伸缩不变性：当数据 \\(x\\) 按照常量 \\(\\lambda\\) 进行伸缩时，得到的规范化后的值保持不变，即：


\\[Norm(W \\lambda x) = Norm(Wx)
\\]
数据伸缩不变性仅仅对BN，LN成立， 因为这两者在对数据进行规范化时，数据进行伸缩其均值和方差也会变化，分子分母相互抵消。



以上是关于深度学习中的学习率设置技巧与实现详解的主要内容，如果未能解决你的问题，请参考以下文章
 

 一文详解深度学习中的Normalization


 [人工智能-深度学习-16]：神经网络基础 - 模型训练超参数 - 学习率（learning rate）


 14 深度学习-卷积


 14 深度学习-卷积


 机器学习概述


 14深度学习-卷积