代码分享：面波数据快速成图

Posted 2023-04-05 mica fish

代码分享：面波数据快速成图

前言

目前，物探数据主要用surfer软件成图，surfer软件具有强大的插值和绘图功能，成图比较美观。但是，生产过程中大量的物探数据，依靠excel和surfer来成图耗费人力时间成本。本博文在MATLAB平台上开发了一套用于面波数据快速成图的小程序，仅供大家借鉴。

文章目录

• 代码分享：面波数据快速成图
• • • • • 前言
  • 1、成图效果展示
  • • • 1.1 原始图像
      • 1.2 高程转换
      • 1.3 里程换算
      • 1.4 图像加工
  • 2、数据读取与图像保存
  • • • 2.1 读取面波视横波速度数据
      • 2.2 数据与图像保存
  • 3、自编函数
  • • • 3.1 dealMBdata函数
      • 3.2 cellcell2mat函数
      • 3.3 sInterp函数
      • 3.4 sLcLabel函数
  • 4、完整代码
  • • • 代码运行过程中如果出现bug，请依据实际工程修改。

1、成图效果展示

1.1 原始图像

对面波数据采用geogiga软件反演，导出视横波数据，在matlab中编辑克里金插值算法的代码，输出图像。

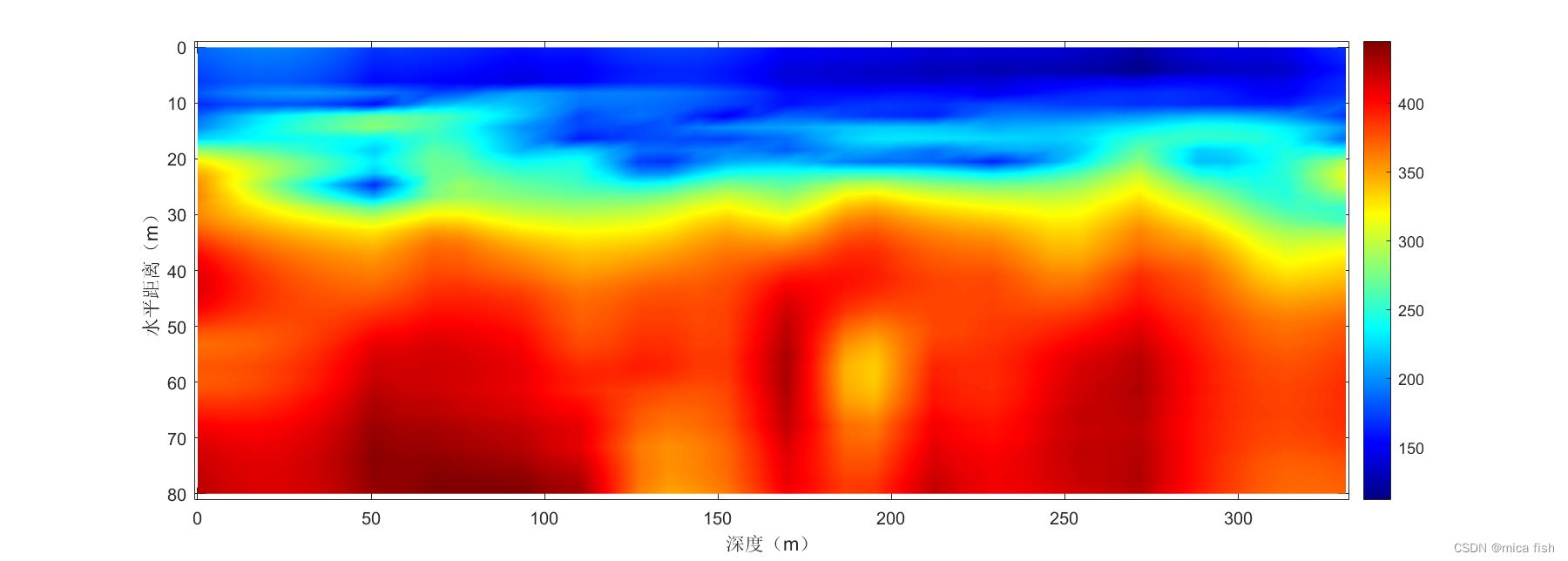
1.2 高程转换

将地表GPS测量的高程，与面波探测的深度进行转换，得到真实的高程。

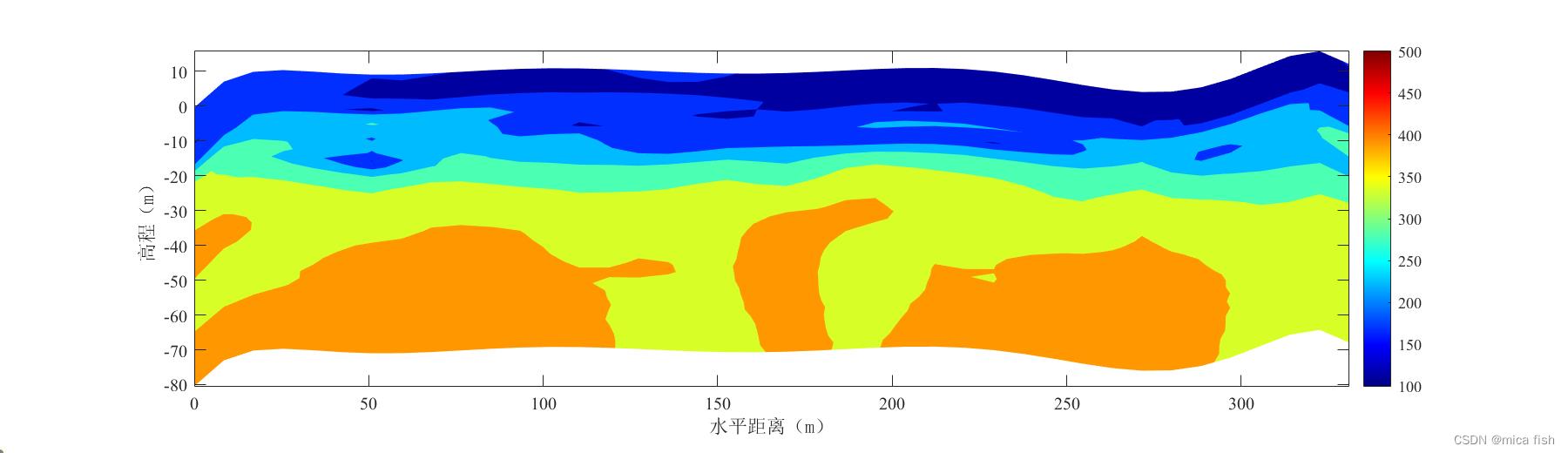
1.3 里程换算

将地表GPS测量的里程与高程，与面波探测的深度和水平距离进行换算，由于面波测点在地表不等距分布，因此里程也是不等间距分布，换算之后得到真实的高程与里程。

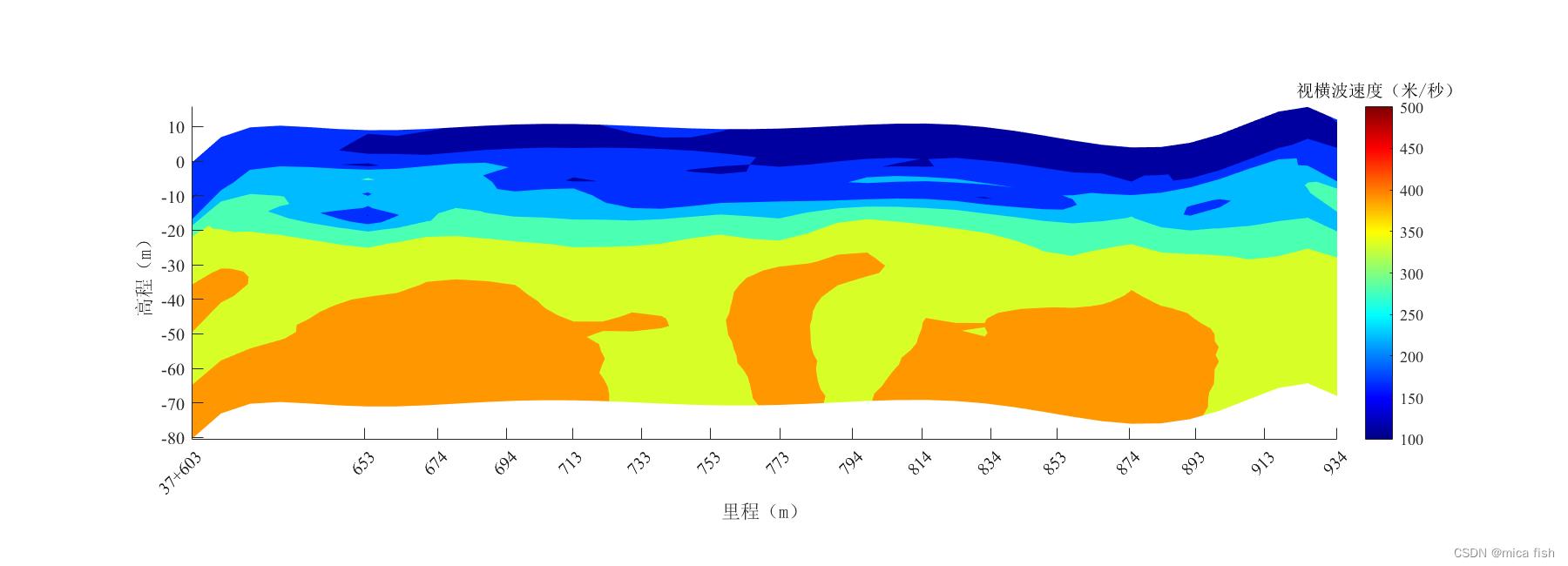
1.4 图像加工

为了得到比较美观的图像，在MATLAB中对图像进行加工。

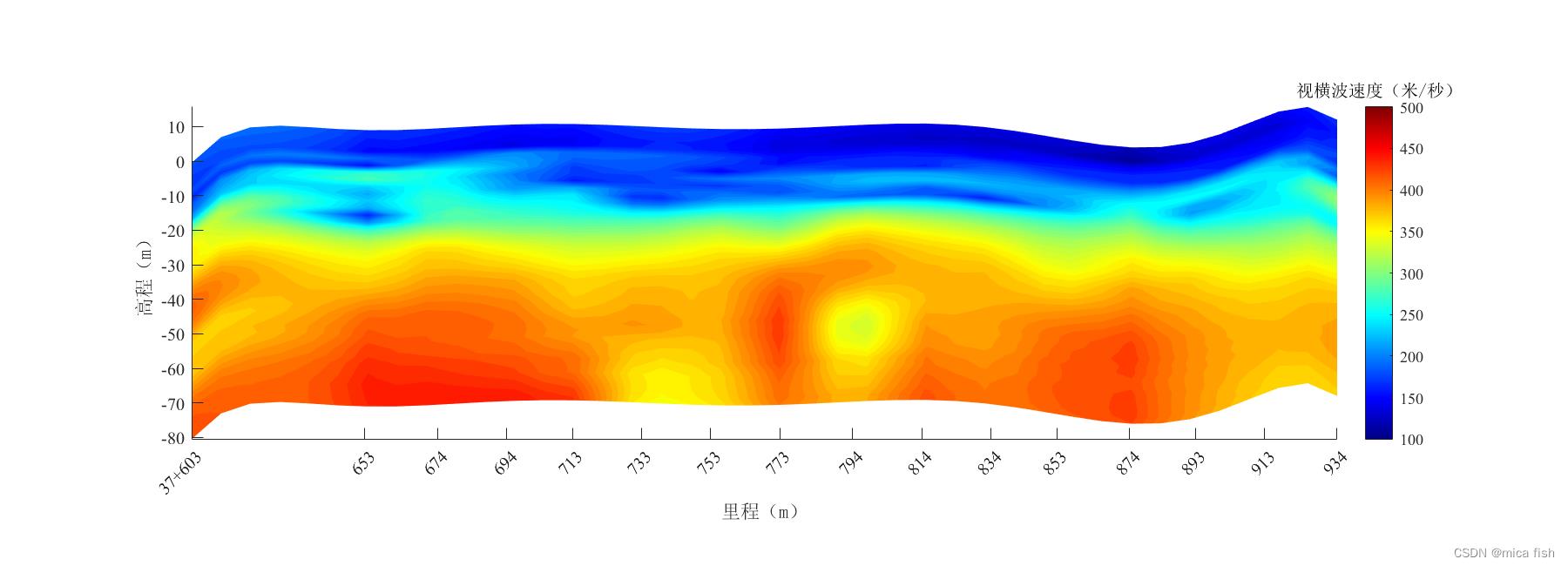
2、数据读取与图像保存

2.1 读取面波视横波速度数据

选择数据文件夹。

% 读取面波数据
[FileName,PathName] = uigetfile('*.txt','请选择视横波速度文件',...
    'MultiSelect','on');
filename = strcat(PathName,FileName);
data = importdata(filename);
fprintf('\\n读取视横波速度完成!\\n请按任意键继续...\\n');

提取数据，自编函数dealMBdata。

% 初始参数设置
% 最大深度
depth_max = 80;
% 插值点数
num_points = 40;

% 面波数据预处理
[points,vs_value,xlocation] = dealMBdata(data);

2.2 数据与图像保存

% 保存数据
clear xx yy zz
xx = X1(:);
yy = Y1_new(:);
zz = YX(:);
C = [xx,yy,zz];
dlmwrite(strcat(PathName,'mianbo.dat'),C);
clear yy
yy = Y1_new(1,:);
high = [xa',yy'];
dlmwrite(strcat(PathName,'gaocheng.dat'),high);

3、自编函数

3.1 dealMBdata函数

function [points,vs_value,xlocation] = dealMBdata(data)
% 此程序为整理面波数据，为克里金插值做准备；
% 输入为读取的面波数据；
% 输出为面波数据点坐标和视横波速度值。
data_sh = data.textdata;  
k = strfind(data_sh,'Location:');
nlie = length(cell2mat(k));
data_sh_length = length(data_sh);

% 数据解译，读出每个频散曲线的起点与长度
%  初始化矩阵
list_begin = ones(1,nlie);
xlocation = ones(1,nlie);
n = 1;
for i = 1:data_sh_length
    if ki
        begin = i+1;
        while kbegin
            begin = begin+1;
        end
        list_begin(n) = begin;
        xlocation(n) = str2double(data_shi,2);
        n = n+1;
    end
end

% 创建克里金插值矩阵
points_length = data_sh_length - nlie - 1;
points = zeros(points_length,2);
vs_value = zeros(points_length,1);
nn = 1;
for i = 1:nlie-1
    A = data_sh(list_begin(i):...
        list_begin(i+1)-2,:);
    A = cellcell2mat(A);
    for j = 1:length(A)
        points(nn,1) = xlocation(i);
        points(nn,2) = A(j,1);
        vs_value(nn) = A(j,2);
        nn = nn + 1;
    end
end
clear A
A = data_sh(list_begin(nlie):...
    end,:);
A = cellcell2mat(A);
points(nn:end,1) = xlocation(nlie);
points(nn:end,2) = A(:,1);
vs_value(nn:end) = A(:,2);

3.2 cellcell2mat函数

function C = cellcell2mat(A)
% 此程序为将嵌套元胞数据转为矩阵
[row,col] = size(A);
C = ones(row,col);
for i = 1:col
    for j = 1:row
        a = cell2mat(A(j,i));
        b = str2double(a);
        C(j,i) = b;
    end
end

3.3 sInterp函数

function [xa,ya] = sInterp(xlocation,data_gc,interp_num,num_points)
a = polyfit(xlocation,data_gc,interp_num);
warning('off');
xa = linspace(min(xlocation),max(xlocation),num_points);
ya = polyval(a,xa);

3.4 sLcLabel函数

function data_lclabel = sLcLabel(data_lc)
n = length(data_lc);
data_lclab = num2str(data_lc);
data_lclabel = cell(n,1);
ak1 = data_lclab(1,:);
data_lclabel1 = strcat(ak1(1:end-3),'+',ak1(end-2:end));
clear ak1 ak2
for i = 2:n
    ak1 = data_lclab(i-1,:);
    ak2 = data_lclab(i,:);
    if strcmp(ak1(1:end-3),ak2(1:end-3))
        data_lclabeli = ak2(end-2:end);
    else
        data_lclabeli = strcat(ak2(1:end-3),...
        '+',ak2(end-2:end));
    end
end

4、完整代码

close all
clear 
clc

% 此程序功能是面波数据快速出图
% 作者：shangxiang
% 时间：2023年2月23日

% 读取面波数据
[FileName,PathName] = uigetfile('*.txt','请选择视横波速度文件',...
    'MultiSelect','on');
filename = strcat(PathName,FileName);
data = importdata(filename);
fprintf('\\n读取视横波速度完成!\\n请按任意键继续...\\n');

% pause;
% 读取GPS测量高程数据
clear FileName PathName
[FileName,PathName] = uigetfile('*.txt','请选择GPS高程文件',...
    'MultiSelect','on');
filename_gc = strcat(PathName,FileName);
data_gc = load(filename_gc);
fprintf('\\n读取高程数据完成!\\n请按任意键继续...\\n');

% 读取GPS测量里程数据
clear FileName PathName
[FileName,PathName] = uigetfile('*.txt','请选择GPS里程文件',...
    'MultiSelect','on');
filename_lc = strcat(PathName,FileName);
data_lc = load(filename_lc);
fprintf('\\n读取里程数据完成!\\n');

% 初始参数设置
% 最大深度
depth_max = 80;
% 插值点数
num_points = 40;

% 面波数据预处理
[points,vs_value,xlocation] = dealMBdata(data);

% 开始克里金插值
% 克里金插值预设参数
theta = [1 1];
lob = [0.1 0.1];
upb = [2 2];
[points_new,vs_value_new] = dsmerge(points,vs_value);
[dmodel,perf] = dacefit(points_new,vs_value_new,@regpoly0,...
    @correxp,theta,lob,upb);
% [dmodel,perf] = dacefit(points,vs_value,@regpoly0,@correxp,theta,lob,upb);
xmin = min(points(:,1));
xmax = max(points(:,1));
XX = gridsamp([xmin 0;xmax depth_max],num_points);
[YX,MSE] = predictor(XX,dmodel);
X1 = reshape(XX(:,1),num_points,num_points);
Y1 = reshape(XX(:,2),num_points,num_points);
YX = reshape(YX,size(X1));

% 对地形数据进行插值，默认插值点数为9，可更改；
interp_num = 9;
[xa,ya] = sInterp(xlocation,data_gc,interp_num,num_points);
Y1_new = -Y1 + ya;

% 对图形进行处理，补充图像下部
% ynew = max(Y1_new(end,:));
% Y1_new = Y1_new(Y1_new > ynew);
% X1 = X1(Y1_new > ynew);
% YX = YX(Y1_new > ynew);
% 处理里程数据
% 获取横坐标位置
data_lcx = data_lc - min(data_lc);
% 获取横坐标刻度
data_lclabel = sLcLabel(data_lc);

% 画图
figure(1);
clear k
k = (depth_max+max(ya))/max(X1(1,:));
set(gcf,'position',[50 150 1200 1500*k]);
% pcolor(X1,Y1_new,YX);
contourf(X1,Y1_new,YX,50,'linecolor','none');
set(gca,'xtick',data_lcx,'xticklabel',...
    data_lclabel,'xticklabelrotation',45);
caxis([100 500]);
colormap(jet);
h = colorbar;
set(get(h,'title'),'string','\\fontname宋体视横波速度（米/秒）',...
    'FontSize',10);
clear a b
axis equal;
box off;
% axis off
shading flat
set(gca,'fontname','times new roman','fontsize',...
    10,'fontweight','normal');
xlabel('\\fontname宋体里程（m）');
ylabel('\\fontname宋体高程（m）');


% 保存数据
clear xx yy zz
xx = X1(:);
yy = Y1_new(:);
zz = YX(:);
C = [xx,yy,zz];
dlmwrite(strcat(PathName,'mianbo.dat'),C);
clear yy
yy = Y1_new(1,:);
high = [xa',yy'];
dlmwrite(strcat(PathName,'gaocheng.dat'),high);

代码运行过程中如果出现bug，请依据实际工程修改。

DFT 平面波方法

DFT 平面波方法

文章目录

• • DFT 平面波方法
  • • 变分法
    • DFT 平面波方法
    • DFT 平面波迭代解法
    • abacus 源码阅读

变分法

考虑薛定谔方程，
$$\hat{H}\psi =E\psi$$
这里的波函数我们一般不能精确得到，所以我们一般找一个数学上可以处理的函数去逼近，
$$\varphi \approx \psi$$
特征值理论告诉我们，极小化能量泛函
$$\tilde{E}=\frac{⟨\varphi |\hat{H}|\varphi ⟩}{⟨\varphi \mid \varphi ⟩}$$
便可以得到最小的特征值 $E_0$（基态能量），此时的 $\varphi$ 也就是对应的特征函数。

如果我们把逼近波函数 $\varphi$ 找一组基底展开，
$$\varphi (\vec{x})=\sum _{i=1}^N{c}_i{\chi }_i(\vec{x})$$
在毕竟波函数单位化约束 $⟨\varphi \mid \varphi ⟩=1$ 的条件下，我们使用拉格朗日乘子法，可以得到广义代数特征值问题，
$$\mathbf{H}\cdot \mathbf{C}=\lambda \cdot \mathbf{S}\cdot \mathbf{C}$$
其中，
$$\begin{array}{rl}{H}_{nm}& =⟨{\chi }_n|\hat{H}|{\chi }_m⟩\\ S_{nm}& =⟨{\chi }_n\mid {\chi }_m⟩\end{array}$$
类比有限元方法，其中的 $S_{nm}$ 是质量矩阵，$H_{nm}$ 可以看成是瑞利泛函意义下的“刚度”矩阵。

DFT 平面波方法

求解 KS 方程
$$\left[{\hat{T}}_s+V_{eff}\right]{\varphi }_i={ϵ}_i{\varphi }_i$$
对波函数进行平面波展开，并对有效势做傅里叶展开，和有限元方法类似，使用平面波基底做测试函数进行变分，忽略一堆推导，最后可以得到一个代数特征值问题，
$$\sum _m{H}_{m^{\prime }m}(\vec{k})c_{i,m}(\vec{k})={ϵ}_i(\vec{k})c_{i,m^{\prime }}(\vec{k})$$
其中，
$$H_{m^{\prime }m}(\vec{k})=\frac{1}{2}{\left|\vec{k}+{\vec{G}}_m\right|}^2{\delta }_{m^{\prime }m}+V_{eff}\left({\vec{G}}_m-{\vec{G}}_{m^{\prime }}\right)$$
第一部分是动能项，比较好理解。第二部分可以进一步细化。略去推导，我们直接给出表达式。

• Hartree 势
  V H ( G ⃗ ) = 4 π n ( G ⃗ ) G 2 V_H(\\vecG)=4 \\pi \\fracn(\\vecG)G^2 以上是关于代码分享：面波数据快速成图的主要内容，如果未能解决你的问题，请参考以下文章

  求一段MATLAB图像批量处理和数据的存储的代码

  MATLAB中如何将一幅图像改为不同的亮度级？

  求一段MATLAB图像批量处理和数据的存储的代码

  在matlab中如何用mat数据作图

  DFT 平面波方法

  MATLAB绘制雷达图/蜘蛛图