TensorFlow的四种交叉熵

Posted 2023-04-05

参考技术A 一种信息化的描述方法，用来定义信息中不确定因素的多少。机器学习结果的好坏评判标准就是两类信息之间的熵最小，由此引发了评判结果好坏的标准。

交叉熵（Cross Entropy）是Loss函数的一种（也称为损失函数或代价函数），用于描述模型预测值与真实值的差距大小，常见的Loss函数就是均方平方差（Mean Squared Error），定义如下。

![][matrix]
[matrix]: http://latex.codecogs.com/png.latex?C= \frac(y-a)^22
​平方差表示预测值与真实值直接相减，为了避免得到负数取绝对值或者平方，再做平均就是均方平方差。注意这里预测值需要经过sigmoid激活函数，得到取值范围在0到1之间的预测值。
平方差可以表达预测值与真实值的差异，但在分类问题种效果并不如交叉熵好，原因可以参考 这篇博文 。
交叉熵的定义如下，
当神经元函数为![][fact]这里
[fact]: http://latex.codecogs.com/png.latex?a= \sigma(z)

01: ![][01]
02: ![][02]
03: ![][03]
04: ![][04]
05: ![][05]
06: ![][06]
07: ![][07]
[00]: http://latex.codecogs.com/png.latex ?\beginbmatrix1&x&x 2\1&y&y 2\1&z&z^2\\endbmatrix
[01]: http://latex.codecogs.com/png.latex?sh(x)= \frace x+e -x2
[02]: http://latex.codecogs.com/png.latex?C_n ^k=\fracn(n-1)\ldots(n-k+1)k!
[03]: http://latex.codecogs.com/svg.latex ?\beginalign\sqrt37&=\sqrt\frac73 2-112 2\&=\sqrt\frac73 212 2\cdot\frac73 2-173 2\&=\sqrt\frac73 212 2\sqrt\frac73 2-173 2\&=\frac7312\sqrt1-\frac173 2\&\approx\frac7312\left(1-\frac12\cdot73 2\right)\endalign
[04]: http://latex.codecogs.com/svg.latex ?\beginarrayc|lcrn&\textLeft&\textCenter&\textRight\\hline1&0.24&1&125\2&-1&189&-8\3&-20&2000&1+10i\\endarray
[05]: http://latex.codecogs.com/svg.latex ?\mathbbN,Z,Q,R,C
[06]: http://latex.codecogs.com/svg.latex ?\left\beginarraylla_1x+b_1y+c_1z&=d_1+e_1\a_2x+b_2y&=d_2\a_3x+b_3y+c_3z&=d_3\endarray\right.
[07]: http://latex.codecogs.com/svg.latex?f \left(\left[\frac1+\leftx,y\right\left(\fracxy+\fracyx\right)\left(u+1\right)+a\right]^3/2\right)

Tensorflow 损失函数及学习率的四种改变形式

Reference: https://blog.csdn.net/marsjhao/article/details/72630147

分类问题损失函数-交叉熵（crossentropy)

        交叉熵描述的是两个概率分布之间的距离，分类中广泛使用的损失函数，公式如下     

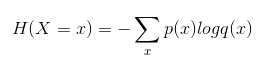
        在网络中可以通过Softmax回归将前向传播得到的结果变为交叉熵要求的概率分数值。Tensorflow中，Softmax回归的参数被去掉，通过一层将神经网络的输出变为一个概率分布。

代码实现

import tensorflow as tf
 
y_ = tf.constant([[1.0, 0, 0]]) # 正确标签
y1 = tf.constant([[0.9, 0.06, 0.04]]) # 预测结果1
y2 = tf.constant([[0.5, 0.3, 0.2]]) # 预测结果2
# 以下为未经过Softmax处理的类别得分
y3 = tf.constant([[10.0, 3.0, 2.0]])
y4 = tf.constant([[5.0, 3.0, 1.0]])
 
# 自定义交叉熵
cross_entropy1 = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y1, 1e-10, 1.0)))
#tf.clip_by_value 将一个tensor元素数值限制在指定范围内,防止一些错误，起到数值检查作用。
cross_entropy2 = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y2, 1e-10, 1.0)))
# TensorFlow提供的集成交叉熵
# 注：该操作应该施加在未经过Softmax处理的logits上，否则会产生错误结果
# labels为期望输出，且必须采用labels=y_, logits=y的形式将参数传入
cross_entropy_v2_1 = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y3)
cross_entropy_v2_2 = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y4)
 
sess = tf.InteractiveSession()
print(‘[[0.9, 0.06, 0.04]]:‘, cross_entropy1.eval())
print(‘[[0.5, 0.3, 0.2]]:‘, cross_entropy2.eval())
print(‘v2_1‘, cross_entropy_v2_1.eval())
print(‘v2_2‘,cross_entropy_v2_2.eval())
sess.close()
 
‘‘‘
[[0.9, 0.06, 0.04]]: 0.0351202
[[0.5, 0.3, 0.2]]: 0.231049
v2_1 [ 0.00124651]
v2_2 [ 0.1429317]
‘‘‘

回归问题损失函数-均方误差（MSE,mean squared error）

       均方误差也可以用于分类问题的损失函数，

           

 

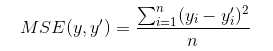
自定义损失函数

        对于如下自定义损失函数的Tensorflow实现

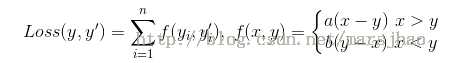
          loss= tf.reduce_sum(tf.where(tf.greater(y, y_), (y-y_)*loss_more,(y_-y)*loss_less))

           tf.greater(x,y),返回x>y判断结果的bool型tensor。 tf.where(condition,x=None,y=None,name=None)根据condition选择x或者y。

代码实现

import tensorflow as tf
from numpy.random import RandomState
 
batch_size = 8
x = tf.placeholder(tf.float32, shape=(None, 2), name=‘x-input‘)
y_ = tf.placeholder(tf.float32, shape=(None, 1), name=‘y-input‘)
 
w1 = tf.Variable(tf.random_normal([2,1], stddev=1, seed=1))
y = tf.matmul(x, w1)
 
# 根据实际情况自定义损失函数
loss_less = 10
loss_more = 1
# tf.select()在1.0以后版本中已删除，tf.where()替代
loss = tf.reduce_sum(tf.where(tf.greater(y, y_),
                               (y-y_)*loss_more, (y_-y)*loss_less))
train_step = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
 
rdm = RandomState(seed=1) # 定义一个随机数生成器并设定随机种子
dataset_size = 128
X = rdm.rand(dataset_size, 2)
Y = [[x1 + x2 +rdm.rand()/10.0 - 0.05] for (x1, x2) in X] # 增加一个-0.05~0.05的噪声
 
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
for i in range(5000):
    start = (i * batch_size) % dataset_size
    end = min(start+batch_size, dataset_size)
    train_step.run({x: X[start: end], y_: Y[start: end]})
    if i % 500 == 0:
        print(‘step%d:
‘ % i, w1.eval())
print(‘final w1:
‘, w1.eval())
sess.close()
 
‘‘‘
loss_less = 10
loss_more = 1
final w1:
 [[ 1.01934695]
 [ 1.04280889]]
loss_less = 1
loss_more = 10
final w1:
 [[ 0.95525807]
 [ 0.9813394 ]]
loss_less = 1
loss_more = 1
final w1:
 [[ 0.9846065 ]
 [ 1.01486754]]
‘‘‘

Tensorflow 的Cross_Entropy实现

      1. tf.nn.softmax_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None,dim=-1,name=Node)

          作用：自动计算logits(未经过Softmax)与labels 之间的cross_entropy交叉熵。logits 为神经网络最后一层的输出，有batch的话，大小为[batchsize,num_classes]，单样本的话就是num_classes。labels：为ground Truth大小同上。labels的每一行为one-hot表示。

     2.tf.nn.sparse_softmax_cross_entropy_with_logits()

         输入的logits是未经缩放的，函数内部对logits进行一个softmax操作。返回值为一个向量，求交叉熵做一步tf.reduce_sum操作，求loss，进一步做tf.reduce_mean，对向量求均值。

    3.tf.nn.sigmoid_cross_entropy_with_logits(_sentinel=None,labels=None,logits=None,name=None)

    4.tf.nn.weithted_cross_entropy_with_logits(targets,logits,pos_weith,name=None)

 

学习率的四种改变形式：

       1.fixed:learning rate 固定不变

       2.Step:在每次迭代stepsize次后，减少gmma倍。lr = lr x gamma

       3. polynomial: 呈多项式曲线下降，lr = base_lr x(t/T)^power

       4. Inv:随着迭代次数的增加而下降。LR = base_lr x(1+gmma x iter)^power