蓝桥杯冲刺并查集专题
Posted Jiong-952
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了蓝桥杯冲刺并查集专题相关的知识,希望对你有一定的参考价值。
并查集
作用:
- 将两个集合合并
- 快速判断两个元素是否在一个集合当中
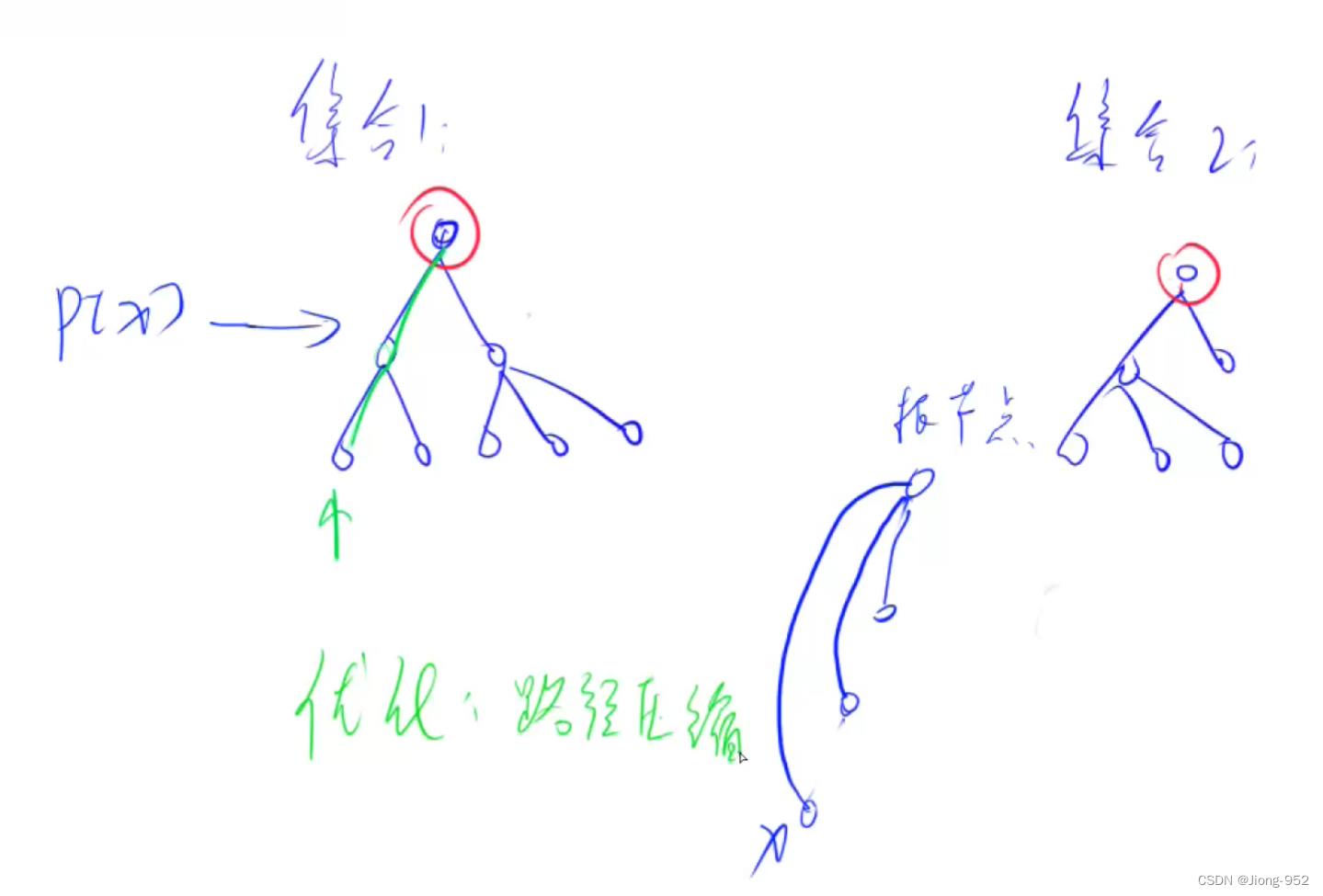
基本原理:每个集合用一个树来表示,树根的编号就是结点的编号,每个结点存储他的父节点,p[x]表示x的父节点
优化:路径压缩
当第一次找x的祖宗结点时发现p[x] != x那么就执行p[x] = find(p[x]) 这样下次找的时候p[x] == x
static int N = 100010;
static int[] p = new int[N], cnt = new int[N]; //p:根节点数组 cnt:记录连通块中结点数目
//并查集初始化
for (int i = 1; i <= n; i++)
p[i] = i;
cnt[i] = 1;
// 把集合x并入y
public static void union(int x, int y)
int px = find(x);
int py = find(y);
cnt[py] += cnt[px];
p[px] = py;
//寻找x的父节点+路径压缩
public static int find(int x)
if(p[x] != x) p[x] = find(p[x]);
return p[x];
// 获得连通块的数目
public static int get_connection()
int k = 0;
for(int i = 1; i <= 7; i++)
if(st[i] && p[i] == i) k++;
return k;
七段码
题目链接:https://www.lanqiao.cn/problems/595/learning/?page=1&first_category_id=1&sort=students_count&name=%E4%B8%83%E6%AE%B5%E7%A0%81
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝要用七段码数码管来表示一种特殊的文字。
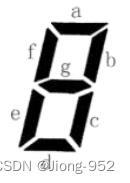
上图给出了七段码数码管的一个图示,数码管中一共有 77 段可以发光的二 极管,分别标记为 ,a,b,c,d,e,f,g。
小蓝要选择一部分二极管(至少要有一个)发光来表达字符。在设计字符 的表达时,要求所有发光的二极管是连成一片的。
例如:b 发光,其他二极管不发光可以用来表达一种字符。
例如 c 发光,其他二极管不发光可以用来表达一种字符。这种方案与上 一行的方案可以用来表示不同的字符,尽管看上去比较相似。
例如:,a,b,c,d,e 发光,,f,g 不发光可以用来表达一种字符。
例如:,b,f 发光,其他二极管不发光则不能用来表达一种字符,因为发光 的二极管没有连成一片。
请问,小蓝可以用七段码数码管表达多少种不同的字符?
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
思路
本题需要判断所有的发光二极管是否属于同一个连通块,因此可以使用并查集,判断是否只有一个连通块
其次,可以使用dfs来枚举每个灯管是否发光,枚举所有状态
具体代码
注意:建图部分要小心仔细
public class Main
static int N = 8,res = 0;
static boolean[] st = new boolean[N];
static int[] p = new int[N];
static boolean[][] e = new boolean[N][N];
public static int find(int x)
if(p[x] != x) p[x] = find(p[x]);
return p[x];
public static void union(int x, int y)
int px = find(x);
int py = find(y);
if(px != py) p[px] = py;
public static void initConnect()
//e[x][y]:表示x和y相联
//建图和初始化并查集
e[1][2] = e[1][6] = true;
e[2][1] = e[2][7] = e[2][3] = true;
e[3][2] = e[3][7] = e[3][4] = true;
e[4][3] = e[4][5] = true;
e[5][4] = e[5][7] = e[5][6] = true;
e[6][5] = e[6][7] = e[6][1] = true;
e[7][2] = e[7][3] = e[7][6] = e[7][5] = true;
public static void init()
for(int i = 1; i <= 7; i++) p[i] = i;
public static void dfs(int u)
if(u > 7)
// 每次都要更新并查集
init();
for(int i = 1; i <= 7; i++)
for(int j = i; j <= 7; j++)
if(st[i] && st[j] && e[i][j]) union(i, j);
if(isValid() == 1) res++;
return;
st[u] = false;
dfs(u+1);
st[u] = true;
dfs(u+1);
return;
// 判断是不是只有一个连通块
public static int isValid()
int k = 0;
for(int i = 1; i <= 7; i++)
if(st[i] && p[i] == i) k++;
return k;
public static void main(String[] args)
initConnect();
init();
dfs(1);
System.out.println(res);
蓝桥侦探
蓝桥:https://www.lanqiao.cn/problems/1136/learning/
对应LeetCode:https://leetcode.cn/problems/possible-bipartition/
题目描述
小明是蓝桥王国的侦探。
这天,他接收到一个任务,任务的名字叫分辨是非,具体如下:
蓝桥皇宫的国宝被人偷了,犯罪嫌疑人锁定在 NN 个大臣之中,他们的编号分别为 1\\sim N1∼N。
在案发时这 NN 个大臣要么在大厅11,要么在大厅22,但具体在哪个大厅他们也不记得了。
审讯完他们之后,小明把他们的提供的信息按顺序记了下来,一共 MM 条,形式如下:
x y,表示大臣 xx 提供的信息,信息内容为:案发时他和大臣 yy 不在一个大厅。
小明喜欢按顺序读信息,他会根据信息内容尽可能对案发时大臣的位置进行编排。
他推理得出第一个与先前信息产生矛盾的信息提出者就是偷窃者,但推理的过程已经耗费了他全部的脑力,他筋疲力尽的睡了过去。作为他的侦探助手,请你帮助他找出偷窃者!
输入描述
第 11 行包含两个正整数 N,MN,M,分别表示大臣的数量和口供的数量。
之后的第 2 \\sim M+12∼M+1 行每行输入两个整数 x , yx,y,表示口供的信息。
1\\leq N,M \\leq 5\\times10^51≤N,M≤5×105,1 \\leq x,y\\leq N1≤x,y≤N。
输出描述
输出仅一行,包含一个正整数,表示偷窃者的编号。
输入输出样例
示例 1
输入
4 5
1 2
1 3
2 3
3 4
1 4
输出
2
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
题解
思路:反向点 + 并查集

图源:LeetCode【宫水三叶】判定二分图模板题的题解
代码
import java.util.Scanner;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改
public class Main
static int[] father;
public static void main(String[] args) throws IOException
StreamTokenizer sc = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
//在此输入您的代码...
sc.nextToken();
int N = (int) sc.nval;
sc.nextToken();
int M = (int) sc.nval;
//并查集
father = new int[2 * N +1];
//初始化
for(int i = 0; i <= 2*N; i++)
father[i] = i;
while(M-- > 0)
sc.nextToken();
int x = (int) sc.nval;
sc.nextToken();
int y = (int) sc.nval;
if(find(x) == find(y))
System.out.println(x);
return;
union(x,y+N);
union(x+N,y);
//寻找根节点
public static int find(int i)
if(father[i] == i) return i;
father[i] = find(father[i]);
return father[i];
//合并集合
public static void union(int x, int y)
int fx = find(x);
int fy = find(y);
if(fx != fy) father[fx] = fy;
蓝桥杯 修改数组 python (并查集)
蓝桥杯 修改数组 python (并查集)
题目描述
给定一个长度为 N N N 的数组 A = [ A 1 , A 2 , ⋅ ⋅ ⋅ , A N A_1,A_2,··· ,A_N A1,A2,⋅⋅⋅,AN],数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A 2 , A 3 , ⋅ ⋅ ⋅ , A N A_2,A_3,··· ,A_N A2,A3,⋅⋅⋅,AN。
当修改 A i A_i Ai时,小明会检查$ A_i 是 否 在 是否在 是否在A_1 ∼ A_i−1$现过。如果出现过,则小明会给 A i A_i Ai加上 1 ;如果新的 A i A_i Ai仍在之前出现过,小明会持续给 A i A_i Ai加 1 ,直 到 A i A_i Ai没有在 A 1 ∼ A i − 1 A_1 ∼ A_i−1 A1∼Ai−1 中出现过。
当 A N A_N AN也经过上述修改之后,显然 A A A 数组中就没有重复的整数了。
现在给定初始的 A A A 数组,请你计算出最终的 A A A 数组。
输入描述
第一行包含一个整数 N N N。
第二行包含 N N N 个整数 A 1 , A 2 , ⋅ ⋅ ⋅ , A N A_1,A_2,··· ,A_N A1,A2,⋅⋅⋅,AN.
其中, 1 ≤ N ≤ 1 0 5 1 \\leq N \\leq 10^5 1≤N≤105, 1 ≤ A i ≤ 1 0 6 1 \\leq A_i \\leq 10^6 1≤Ai≤106。
输出描述
输出 N N N 个整数,依次是最终的 A 1 , A 2 , ⋅ ⋅ ⋅ , A N A_1,A_2,···,A_N A1,A2,⋅⋅⋅,AN。
输入输出样例
示例
输入
5
2 1 1 3 4
输出
2 1 3 4 5
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
思路
简单的思路可以利用哈希表,类似于bool数组,如果出现了,就进行了+1得到一个,如果发生矛盾了就需要遍历整个数组,在复杂的情况下,就需要n方的复杂度,对于很大的数据这就不太现实。
可以利用并查集,这样我们得到数据就只需要O(1)就解决了
首先设置一个father数组,这个数组所有的元素都指向自身,f[i]表示当你访问到 i 个数时应该把他换成什么
一开始都是f[ i ] 指向i ,也就说明都没访问过
当你访问了 i 以后,就需要进行更新,更新f[i] = f[i+1]
因为有时候有些数据是重复的,所以当我们再次访问到i的时候,i已经输出过了,这时候我们需要输出的i+1
但是这也涉及一个问题,i+1也有可能输出过了,所以说我们就输出的是f[i+1]
代码code
# https://www.lanqiao.cn/problems/185/learning/
import os
import sys
# 并查集 用于处理元素分组 寻找父亲
def find(x):
global fa
if fa[x] != x:
fa[x] = find(fa[x])
return fa[x]
N = int(input())
A = list(map(int,input().split()))
# 首先创建数组大小的并查集序列 自循环 全部指向自己
fa = [i for i in range(1000001)]
for i in range(N):
# 找到A[i]元素父亲
# 如果A[i]元素没有找到 则返回A[i]的值 同时将下一次查到A[i]值指向A[i]指向下一位
# 如果A[i]找到 则继续增加
# 2 1 1 3 4
# 首先2 的父亲是2 并同时把父亲数组中A[i]位置元素修改为3,也就是再遇到2的时候,换为3
# 其次为1 1的父亲是1 同时把父亲数组中1位置元素修改为2
# 获得1 1的父亲此时为3 输出3 并将3的父亲修改为4
# 获得3 3的父亲此时为4 输出4 并将此时3的父亲修改为5
# 获得4 4的父亲此时为5 输出5 并将此时5的父亲修改为6
A[i] = find(A[i])
fa[A[i]] = find(A[i] + 1) # 更新为下一个点指向的点
for i in range(N):
print(A[i], end=" ")
以上是关于蓝桥杯冲刺并查集专题的主要内容,如果未能解决你的问题,请参考以下文章