多尺度空间-光谱相互作用Transformer:Pan-Sharpening
Posted 小郭同学要努力
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了多尺度空间-光谱相互作用Transformer:Pan-Sharpening相关的知识,希望对你有一定的参考价值。
Multiscale Spatial–Spectral Interaction Transformer for Pan-Sharpening
(用于泛锐化的多尺度空间-光谱相互作用Transformer)
基于深度神经网络(DNN)的泛锐化方法已经产生了最先进的融合性能。然而,基于DNN的方法主要集中在利用卷积神经网络对低空间分辨率多光谱(LR MS)和全色(PAN)图像的局部特性进行建模。映像中的全局从属关系将被忽略。为了同时捕捉图像的局部和全局特性,我们提出了一种多尺度空间-光谱交互作用Transformer(MSIT) 用于全色锐化。具体地说,我们构造了包含卷积变换编码器的多尺度子网络,以分别从LR MS和PAN图像中提取不同尺度下的局部和全局特征。然后,设计空间-光谱交互作用注意模块(SIAM)来合并每个尺度上的特征。在SIAM中,交互注意力被用来有效地解耦空间和光谱信息,以增强所提取特征的互补性和减少冗余。来自不同尺度的特征被进一步集成到多尺度重建模块(MRM) 中以生成期望的高空间分辨率多光谱图像,其中空间和光谱信息被逐尺度地融合。在降维和全尺度数据集上的实验表明,与现有方法相比,该方法在可视化和数值分析方面具有更好的效果。
Introduction
高空间分辨率多光谱(HR-MS)图像包含丰富的空间和光谱信息,对于环境监测、土地调查等记录场景的判读具有重要意义。然而,由于成像技术的限制,遥感图像很难同时达到空间和光谱两种分辨率。大多数卫星,如QuickBird和GeoEye1,只捕获高空间分辨率全色(PAN)和低空间分辨率多光谱(LR MS)图像。因此,采用全色锐化技术整合PAN和MS图像中的空间和光谱信息,以生成HR MS图像。
二十多年来,提出了很多泛锐化的方法。根据它们的范式,这些方法可以分为四类:基于组件替换(CS)的方法、基于多分辨率分析(MRA)的方法、基于模型的方法和基于深度神经网络(DNN)的方法。对于第一类,使用一些线性变换将上采样的LRMS图像投影到一个新的空间,在该空间中LRMS图像被分解为空间和光谱分量。然后,用直方图匹配的PAN图像代替LR MS图像的空间分量。最后,对新分量进行逆变换,得到高分辨质谱图像。基于CS的方法通常考虑强度-色调-饱和度(IHS)、主成分分析(PCA)和Gram-Schmidt(GS)变换以用于LR MS图像的锐化。为了自适应估计LR MS图像的空间分量,提出了自适应GS(GSA),其中通过最小化均方误差来计算组合权重。为了有效地增强LR MS图像的不同波段中的空间细节,提出了一种波段相关空间细节(BDSD)模型,其中自适应地估计不同波段的组合权重。最近,Vivone等人开发了BDSD的鲁棒版本以获得更好的融合结果。此外,Choi等人提出了部分替换自适应CS(PRACS),其中LR MS图像的空间分量被PAN图像部分替换。对于第一种方法,其实现简单明了。然而,这些方法的融合结果普遍存在光谱失真。
对于基于MRA的方法,假设可以从对应的PAN图像中找到在LR MS图像中丢失的空间信息。因此,将多分辨率分解应用于PAN图像以提取空间细节。然后,将这些细节注入到上采样的LR MS图像中以产生泛锐化图像。在这一类别中,高通滤波器被设计用于提取空间信息,例如Indusion 和广义拉普拉斯金字塔(GLP)。通过集成调制传递函数(MTF),提出了MTF-GLP,用于更准确地提取空间细节。然后,通过结合高通调制(HPM)进一步扩展MTF-GLP。此外,还引入了一些先进的MRA工具来表示PAN和LR MS图像中的空间信息。例如,Shah等人利用非下采样轮廓波(NSCT)来增强LR MS图像中的空间细节。根据分解框架,构建了一些类似MRA的滤波器以推断更合理的空间信息。基于MRA的方法的融合图像在光谱信息方面表现出更好的保留,因为只有空间细节被注入到上采样的LR MS图像中。然而,它们的融合图像的空间性能高度依赖于在经验过程中设计的滤波器。滤波器的设计应考虑成像传感器的MTF。
基于模型的方法,假设LR MS图像是HR MS图像通过空间退化的结果。类似地,PAN图像被认为是HR MS图像的光谱退化结果。因此,源图像和HR MS图像之间的关系可以在空间和光谱退化模型中编码。然后,通过求解源图像和HR MS图像之间的空间和光谱退化模型来获得期望的HR MS图像。为了正则化空间和光谱退化模型的解空间,采用各种先验作为正则化。例如,作为一种流行的先验,稀疏性被广泛研究。Zhang等人设计了一个结构稀疏项,用于空间和光谱退化模型的正则化。Palsson等人将全变差(TV)正则化与上述模型相结合,以融合LR MS和PAN图像。此外,为了找到更有效的先验,Liu等人探索了图像梯度域中的Hessian先验。Ballester等人还提出了一种变分方法P + XS来融合LR MS和PAN图像。有效的先验将对空间和光谱模型的解空间具有强约束。在有效先验的帮助下,可以估计更准确的HR MS图像。然而,在复杂的场景中,这些方法中采用的先验可能是无效的,从而限制了它们的推广。此外,基于模型的方法通常通过迭代优化算法来求解。因此,其复杂性不容忽视。
近年来,DNN在许多领域引起了极大的关注,特别是在计算机视觉任务中,由于其强大的学习能力。对于泛锐化,基于DNN的方法也呈现出最先进的融合性能。Masi等人首先提出了一种泛锐化神经网络(PNN),其灵感来自中的超分辨率卷积神经网络(CNN)。然后,进一步提出了改进的PNN(APNN),以提高PNN的性能。作为一个有效的框架,残差学习用于描述MS图像中的空间结构。例如,Yang等人将残差网络(ResNet)学习的空间细节注入到上采样的LR MS图像中。Wei等人通过残差学习开发了一种深度卷积神经网络,以提高融合结果的准确性。考虑到真实的图像和虚假图像的分布之间的极小极大博弈,还考虑了生成对抗网络(GAN)来融合LR MS和PAN图像。Liu等人采用GAN合成HR MS图像,并建立了两个子网络从LRMS和PAN图像中提取特征。为了减轻对监督数据集的需求,Ma等人采用了两个鉴别器来区分融合图像中的空间和光谱信息。Diao等人提出了一种多尺度GAN框架来逐步生成融合图像,并通过相应的鉴别器对融合图像进行逐尺度鉴别。
尽管DNN在泛锐化方面取得了成功,但由于有限的感受野,基于DNN的方法仅关注图像的局部属性。因此,基于DNN的泛锐化方法难以有效地捕获图像之间的全局相似性,这使得这些方法无法对LR MS和PAN图像中的各种空间和光谱结构进行建模。为了学习图像中的全局信息,通过引入自注意机制开发了一种transformer。到目前为止,transformer在高层次和低层次的视觉任务中表现出巨大的潜力。例如,Yang等人采用变换器来学习低分辨率图像的超分辨率的相关纹理。Chen等人提出了一种预训练的transformer模型,该模型在超分辨率和去噪方面具有最先进的性能。此外,不同尺度下的图像的内容由不同的全局相似性反映。因此,应组合不同尺度下的全局相似性以重建HR MS图像。
为了利用在不同尺度的局部和全局属性,我们提出了一个多尺度的空间-光谱相互作用transformer(MSIT)整合的多尺度特征映射泛锐化。首先,分别从PAN和LR MS图像中提取基于卷积变换编码器的两个多尺度子网络的特征。为了有效地融合来自两个不同尺度的子网络的信息,我们设计了一个空间-光谱交互注意模块(SIAM)。通过空间和光谱注意力的交互作用,减少了两个子网络特征之间的冗余度,同时增强了它们之间的互补性。最后,一个多尺度重建模块(MRM)的构建,以产生融合图像。在该模块中,不同尺度的特征被从粗到细地融合,以恢复融合图像中的空间和光谱信息。在不同数据集上的实验结果表明,所提出的MSIT产生更好的融合结果的客观和主观评价相比,经典和国家的最先进的方法。据我们所知,这是第一个基于Transformer的泛锐化探索PAN和LR MS图像的空间光谱特征,通过相互作用的注意机制。
贡献
1)为了同时对局部和全局依赖关系进行建模,我们设计了多尺度卷积变换子网络。PAN和LR MS图像中的空间和光谱特征提取尺度由子网络的局部和全局相似性信息的描述。
2)我们提出了一个空间-光谱交互注意模块,以整合来自不同子网络的功能。在SIAM中,通过自注意机制提取PAN和LR MS图像的级联特征中的空间信息。以相同的方式,强调LR MS图像中的光谱信息。通过SIAM,减少冗余和增强这些特征之间的互补性。
3)为了有效地整合局部和全局信息的功能在不同的尺度上,我们构建了一个多尺度重建模块。在MRM中,不同尺度的特征内容被继承到融合图像中,以恢复细微的空间和光谱信息。
方法
提出的MSIT框架如图1所示。该网络由两个子网络、三个空间-光谱相互作用注意模块和一个多尺度重建模块组成。
首先,通过与多尺度变换器结构相同的子网络学习PAN图像P ∈
R
H
×
W
R^H×W
RH×W和LR MS图像L ∈
R
H
×
W
×
B
R^H×W×B
RH×W×B的空间和光谱特征。每个子网络由一个基本卷积块和三个卷积变换器(CT)编码器组成。基本卷积块被引入以根据LR MS和PAN图像中的谱带数目来调整差异。H和W分别是图像的高度和宽度。B是MS图像中的条带数。n表示过滤器的数量,经验上设定为32个。s = 2是卷积步长。对于不同子网中提取的特征,分别在空域和谱域对场景信息进行编码。然后,利用SIAM算法对来自不同子网络的空间和光谱信息进行有效融合。该模块利用交互注意力将空间-光谱特征进行组合,避免了特征间的冗余。最后,将不同尺度的SIAM的输出馈送到MRM中,用于重构融合图像H。
Multiscale Convolution–Transformer Encoder
在图1中,我们设计了两个用于特征提取的子网络。子网络由级联的CT编码器组成。LR MS和PAN图像首先被馈送到第一卷积层中以获得具有相同数量的通道的特征图。然后,空间和光谱特征通过CT编码器按比例学习。CT编码器的结构如图2a所示。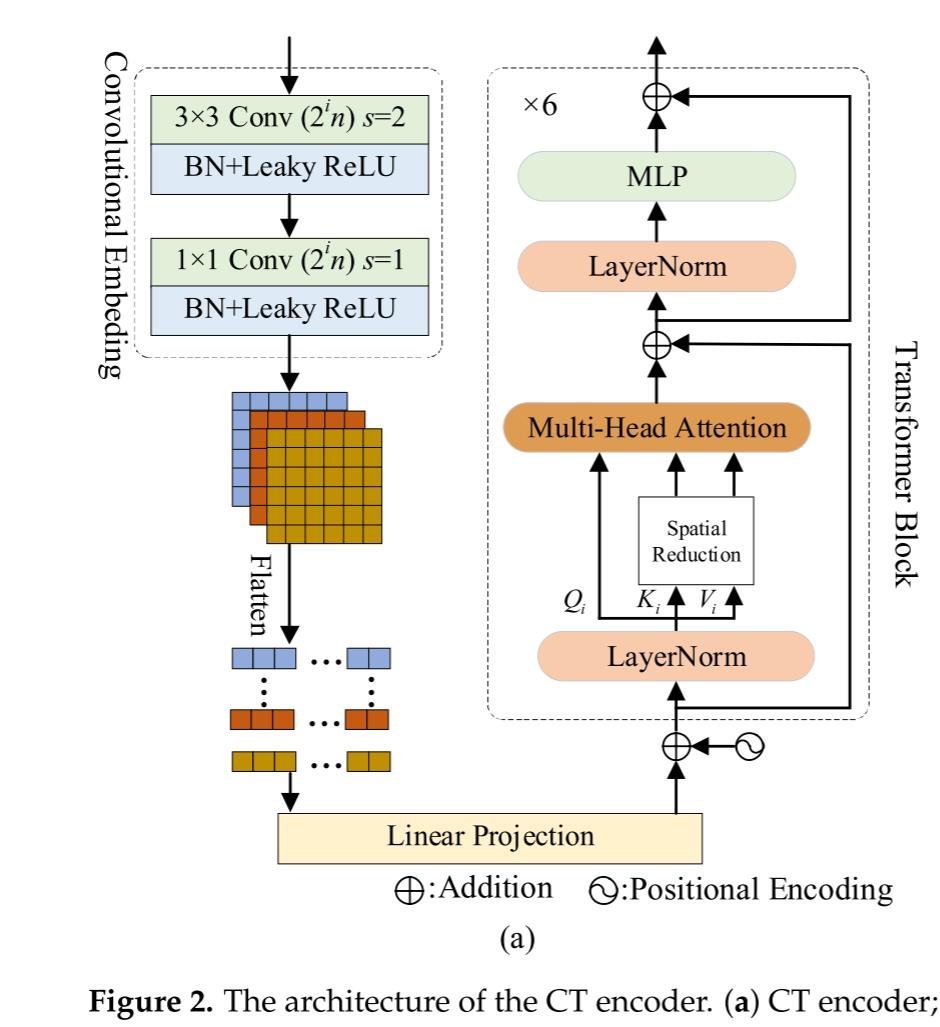
对于子网络中的第i个CT编码器,大小为H/
2
i
2^i
2i×H/
2
i
2^i
2i×
2
i
−
1
2^i-1
2i−1n首先被送入到一个卷积嵌入块。i是CT编码器的索引或者尺度。特别是,卷积嵌入块中的两个卷积层的步长分别是2和1。y.批量归一化(BN)也被引入到卷积嵌入块中。然后,将特征图嵌入到大小为H/
2
i
+
1
2^i+1
2i+1×H/
2
i
+
1
2^i+1
2i+1×
2
i
2^i
2in的粗尺度中。在子网络中,特征图的数量随着尺度数量的增加而增加,以更有效地学习空间和光谱特征。同时,卷积嵌入块捕获输入图像的局部特性。在卷积嵌入之后,如图2a所示的六个Transformer块用于学习图像中的全局依赖性。首先,来自卷积嵌入块的特征图被平坦化并投影为具有位置信息的嵌入特征。在Transformer块中,线性投影首先与位置信息相加,然后被馈送到层归一化(LayerNorm)。LayerNorm可以写为:
此外,为了降低具有大尺寸的特征图的计算成本,考虑了具有空间缩减的多头注意力(SRA)来对不同子空间中的LRMS和PAN图像的表示进行建模。Ki 和Vi首先被馈送到SRA中以减小它们的大小,具体地说是减小Ki和Vi中的行数。然后,Qi和SRA的输出被视为多个头部注意模块的输入,以计算它们之间的注意力。因此,SRA被引入到图2a中以减少计算成本,并且SRA算子在图2b中示出。

通过第i个CT编码器的SR,我们经由SR S(·)算子缩减 Key Ki和Value Vi的大小:
对于子网络中的三个级联CT编码器,我们将下采样比率ri设置为4、2和1。通过设置,不同比例尺的特征图大小将相同。
当我们获得Ki和Vi的简化版本时,根据Wang等人提出的注意力机制的计算,第i个CT编码器中的SRA可以通过下式计算:

最后,这些特征流入多层感知(MLP)。在CT编码器中,可以有效地描述LR MS和PAN图像中的局部和全局信息,这有助于融合图像的空间和光谱保持。
Spatial–Spectral Interaction Attention Module
在MSIT中,通过子网络从PAN和LR MS图像中提取特征图。对于现有的基于DNN的方法,没有明确的注意机制来保证子网络之间的交互。因此,这将导致这些特征之间的一些冗余信息。为了有效地融合空间和光谱特征,我们设计了一个新的注意力模块SIAM,如图3所示。
在SIAM中,首先展开子网络的第i个尺度上的特征图
F
i
F^i
FiP和
F
i
F^i
FiL。在前两个CT编码器中,展开算子的核大小为4 × 4,步长为4。对于最后一个CT编码器,我们将展开算子的内核大小设置为1×1。然后,通过线性投影和层归一化获得它们对应的Key
K
i
K^i
KiP和
F
i
F^i
FiP的Value
V
i
V^i
ViP: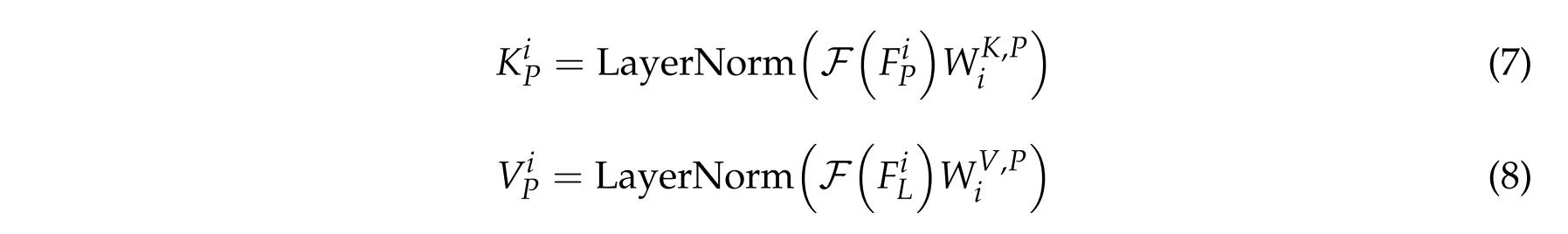
其中F(·)表示展开算子。
K
i
K^i
KiP和
V
i
V^i
ViP分别是
W
K
,
P
W^K,P
WK,Pi和
W
V
,
P
W^V,P
WV,Pi的线性投影后的相应结果。类似地,通过线性投影矩阵
W
K
,
L
W^K,L
WK,Li和
W
V
,
L
W^V,L
WV,Li。我们从LR MS图像的子网络产生
K
i
K^i
KiL的Key
K
i
K^i
KiL和Value
V
i
V^i
ViL。对于Query
Q
i
Q^i
QiC,通过下式从
F
i
F^i
FiP和
K
i
K^i
KiL的级联估计:
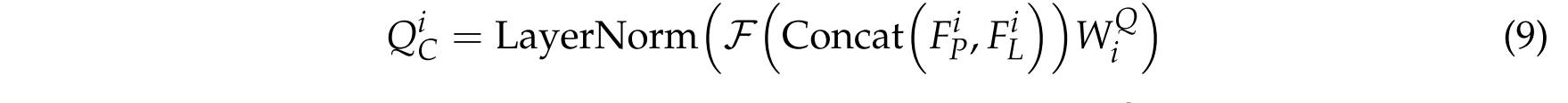
其中级联操作由Concat(·)表示。
W
Q
W^Q
WQi是Concat(
F
i
F^i
FiP,
K
i
K^i
KiL)的线性投影矩阵。然后,子网络之间的空间-频谱交互通过以下方式实现:
以相同的方式,光谱信息由等式(11)进一步突出显示。经过
Q
i
Q^i
QiC的注意力估计,这些特征的冗余度降低,互补性进一步增强。最后,与交互注意的功能折叠和连接在一起的融合图像的生成。
Multiscale Reconstruction Module
当空间和光谱特征融合SIAM在不同的尺度,我们提出了一个MRM从这些功能生成所需的HR MS图像。MRM的架构如图4所示。
在MRM中,粗尺度的特征图通过由卷积和像素混洗组成的块逐步上采样。在该块中,像素混洗用于特征图的上采样,并且上采样率是2或4,这由尺度索引决定。MRM中使用的激活函数为LeakyReLU: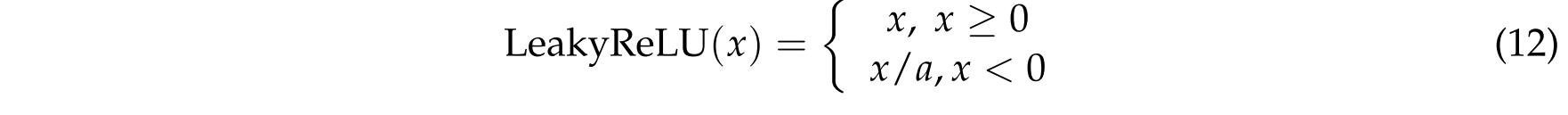
其中x是特征图中的元素,α是预设参数。在特征图被馈送到像素混洗算子之前,特征图中的通道的数量通过先前的卷积层来改进,以增强空间和光谱信息。与传统的上采样方法相比,像素混洗在分辨率提高任务中具有更好的重建性能。然后,将上采样的特征图与精细尺度下的特征图组合以恢复HR MS图像中的空间和光谱细节。通过按尺度融合,精细尺度的特征图被连接以产生HR MS图像。
Optimization
最后,通过最小化损失来学习所提出的MSIT:

其中LFusion代表损失函数。Rm和Fm分别是参考图像和融合图像。M表示训练图像的数量。具体而言,所提出的MSIT在PyTorch框架上进行训练。此外,我们使用Adam优化器来最小化等式(13)中的损失。批次大小设置为4。学习率和历元数分别设置为0.0001和2000。当所提出的MSIT被训练时,LR MS和PAN图像被馈送到模型中以产生泛锐化MS图像。
总结
在本文中,我们提出了一种新的泛锐化方法的基础上的多尺度空间光谱相互作用变换(MSIT)。为了捕获PAN和LR MS图像中的局部和全局属性,子网络由一系列用于特征提取的多尺度CT编码器构建。然后,SIAM被设计成集成来自子网络的特征。在SIAM中,不同子网络的特征之间通过注意机制实现交互,增强了空间和光谱特征之间的互补性,减少了冗余。最后,在不同尺度的空间和光谱特征被送入MRM的融合图像的重建。在MRM中,粗尺度的特征图被逐渐上采样以与细尺度的对应物相联合收割机。通过MRM的体系结构,可以有效地融合不同尺度的空间和光谱信息。从GeoEye-1和QuickBird卫星减少和全尺寸数据集的实验表明,所提出的MSIT的有效性,在客观和主观评价。该网络采用的多尺度变换器可以很容易地用于其他相关任务的特征提取,如遥感图像超分辨率。对于未来的工作,transformer更有效的结构将被探索,以减少所提出的方法的训练和测试时间。此外,所提出的方法不能有效地保留光谱信息,在一些地区包含丰富的颜色信息,这可能是造成的信息损失MRM。因此,我们还将研究更有效的重建模块,以整合特征图中的空间和光谱信息。
图像融合基于matlab粒子群优化自适应多光谱图像融合含Matlab源码 004期
一、图像融合简介
1 图像融合的具体步骤
(1)对全色图像和多光谱图像进行图像预处理,包括图像滤波、重采样、图像配准。
(2)将预处理后的多光谱图像fmul进行IHS变换,分别得到fmul-i(亮度)、fmul-h(色调)、fmul-s(饱和度)3个分量。
(3)对全色图像fpan和多光谱图像亮度分量fmul-i进行J层Contourlet变换,得到以下分量:
其中,AJ表示低频分量;Djk表示各尺度上各方向的高频分量;j=1,…,J,表示分解层次;k=1,…,2lj,表示第j层的各个方向。
(4)对Contourlet变换分解后的低频系数和高频系数分别进行融合,对低频系数采用基于粒子群优化的自适应加权融合规则,对高频系数采用基于粒子群优化的区域结构相似度融合规则,得到满足融合要求的低频和高频分量。
(5)通过Contourlet逆变换得到新的亮度分量fmul-i′,最后对新的亮度分量fmul-i′以及多光谱图像分量fmul-h与fmul-s进行IHS逆变换得到融合图像。
2 低频系数融合规则
Contourlet变换分解后的低频系数反映了源图像的近似信息,它包含了源图像的平均特征、光谱信息和绝大多数的能量信息,决定了融合图像的近似轮廓。低频系数融合的目的是在有效保持多光谱图像的光谱能量信息的基础上适当地融入全色图像的特征信息。目前较为常用的低频系数融合规则有加权平均法、绝对值取大(小)法以及标准差取大法,这些方法直观、简单且速度快,但是未能准确地在多光谱图像的光谱信息和全色图像的空间信息中进行优化选择。因此,本文提出了一种结合粒子群优化算法的低频系数融合规则,以线性加权值作为需要优化的决策变量,以信息熵和相对偏差之间的差值作为目标适应度函数,通过粒子群优化算法的进化迭代自适应地寻找最优加权融合系数。具体融合规则如下:
其中,AJfnew-i表示融合后的低频分量;w1,w2表示加权系数;AJfpan表示全色图像fpan的低频分量;AJfmul-i表示多光谱图像亮度分量fmul-i的低频分量。
基于粒子群优化算法的低频系数融合,以信息熵和相对偏差之间的差值作为目标适应度函数,通过粒子群优化算法迭代寻找信息熵与相对偏差的差值最大时的最优加权系数w1和w2。目标适应度函数=信息熵(E)-相对偏差(RD),其中信息熵为融合图像的信息熵,是基于信息量的评价;相对偏差为融合图像与原多光谱图像之间的相对偏差,是基于光谱性能的评价。为搜索最优的加权系数,粒子群优化算法的参数设置如下:c1为0.01,c2为0.02,惯性权重ω为0.02,种群大小为20,最大迭代次数为600。
3 高频系数融合规则
高频系数反映源图像的细节信息,主要包含边缘、纹理、亮线和区域等特征信息,而单一的图像像元不能很好地表征这些特征信息,因此需要结合多源图像对应像元之间的关系进行综合考虑与分析,通过这一区域特征的多个像元来进行表征和体现。高频系数融合的目的是在保持较优的光谱特性的基础上更多地保留原全色图像的空间细节信息。本文参考文献[19] 对高频系数采用基于区域结构相似度的融合规则进行融合的思想,在此基础上利用粒子群优化算法的全局寻优能力寻找出区域结构相似度的最优阈值p来进行高频系数的融合,融合规则如下。
(1)利用粒子群优化算法寻找高频系数间结构相似度的最优阈值p,以确定高频系数融合的方式。在本文提出的算法中,以融合图像和全色图像之间的结构相似度(SS)作为目标适应度函数,通过粒子群优化算法迭代寻找结构相似度最大时的阈值p,再采用基于区域结构相似度的融合规则进行融合。粒子群优化算法的参数设置如下:c1为0.01,c2为0.02,惯性权重ω为0.6,种群大小为20,最大迭代次数为300。
(2)对高频方向子带进行窗口运算,计算它们对应区域的结构相似度,并记录相似度的值。
(3)若相似度小于p,则采用标准差最大原则进行融合,公式为:
若相似度大于p,采用以下加权融合规则,公式为:
其中,std表示邻域窗口内系数标准差;j表示分解层次,j=1,…,J;k表示第j层的各个方向,k=1,…,2lj;SSIMjk(fpan,fmul-i)为fpan和fmul-i对应区域的结构相似度;E1jk和E2jk分别为fpan、fmul对应区域的权值。
当两幅源图像对应区域的结构相似度小于最优阈值p时,说明图像相关性较小,采用区域方差最大的融合方式可以尽可能多地增加融合图像的细节信息;当两幅源图像的对应区域的结构相似度大于阈值最优p时,说明两幅图像相关性较大且比较相似,采用加权平均融合方式可以更多地保留源图像所共有的区域结构特征。两幅图像X、Y的结构相似度定义如下:
其中,mX和mY分别表示图像X、Y的均值;σX2和σY2分别表示图像X、Y的方差;βXY表示图像X、Y的协方差;L(X,Y)、C(X,Y)和S(X,Y)分别表示图像X、Y的亮度、对比度、结构比较;C1、C2、C3为小的常数,以避免式中分母为零时出现不稳定现象。
二、部分源代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
clear;
close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 加载图像和预处理步骤
addpath QuickBird_Data %% 数据集路径
load PAN; %% 加载 PAN 图像
load MS; %% 加载 MS 图像
%% 使 PAN 和 MS 数据准备好进行处理
MSWV_db = double(MS);
PANWV_db = double(PAN);
MS_ORG = double(MS);
%% 调整大小,将 MS 数据上采样到 PAN 的大小
MSWV_US = imresize(MSWV_db, 1/4, 'bicubic');
MSWV_US = imresize(MSWV_US, 4, 'bicubic');
MSWV_DG = MSWV_US;
PANWV_DS = imresize(PANWV_db, 1/4, 'bicubic');
PANWV_US = imresize(PANWV_DS, 4, 'bicubic');
%% 分离光谱带
R = MSWV_US(:,:,1);
G = MSWV_US(:,:,2);
B = MSWV_US(:,:,3);
NIR = MSWV_US(:,:,4);
%%数据规范化
for i=1:size(MSWV_US,3)
bandCoeffs(i) = max(max(MSWV_US(:,:,i)));
MSWV_US(:,:,i) = MSWV_US(:,:,i)/bandCoeffs(i);
end
P = PANWV_DS;
panCoeff = max(max(P));
P = P/panCoeff;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 问题定义
CostFunction=@(x) ERGAS_Index(x); % 成本函数
nVar = 4; % 决策变量的数量
VarSize = [1 nVar]; % 决策变量矩阵的大小
VarMin = 0; % 变量的下界
VarMax = 1; % 变量的上限
三、运行结果



四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社,2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社,2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社,2015.
[5]谷志鹏,贺新光.Contourlet变换与粒子群优化相耦合的遥感图像融合方法[J].计算机科学. 2016,43(S2)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
以上是关于多尺度空间-光谱相互作用Transformer:Pan-Sharpening的主要内容,如果未能解决你的问题,请参考以下文章