数据结构之Go实现遍历二叉树
Posted 韜の道
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构之Go实现遍历二叉树相关的知识,希望对你有一定的参考价值。
文章目录
二叉树的基础知识
(1)二叉树的定义
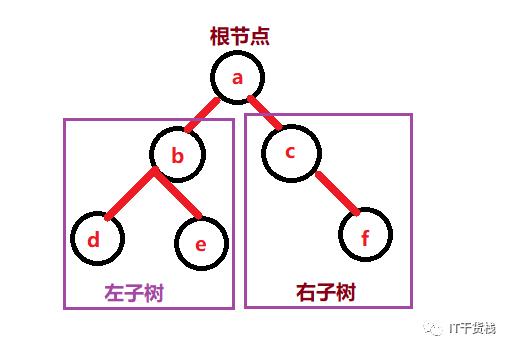
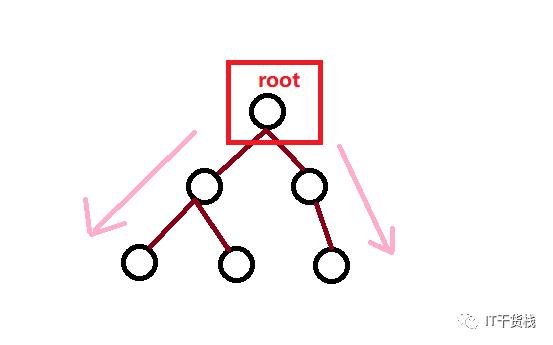
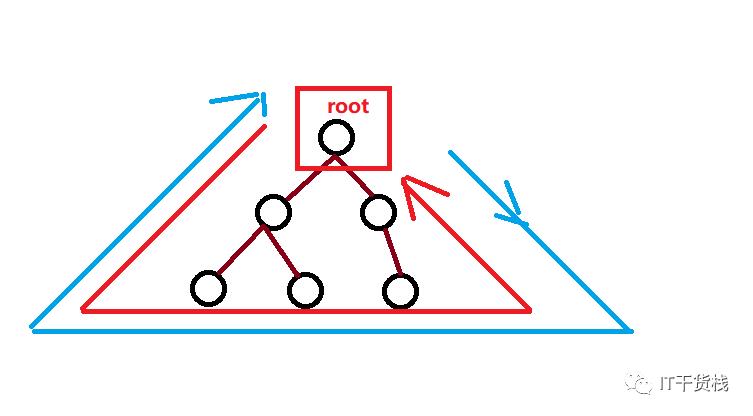
二叉树是 n 个有限元素的集合,该集合或者为空、或者由一个称为根( root )的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树,在二叉树中,一个元素也称作一个节点 。
二叉树是将一般的树加上以下的两个限制条件:
-
每个结点最多只有两棵子树,即二叉树中结点的度只能为 0、1、2;
-
子树有左右顺序之分,不能颠倒。
根据二叉树的定义可知,二叉树共有 5 种基本形态:空二叉树、只有根结点、只有左子树,右子树为空、只有右子树,左子树为空、既有左子树,又有右子树。
(2)特殊类型
-
满二叉树:如果一棵二叉树只有度为 0 的节点和度为 2 的节点,并且度为 0 的节点在同一层上,则这棵二叉树为满二叉树。
-
完全二叉树:深度为 k ,有 n 个节点的二叉树当且仅当其每一个节点都与深度为 k 的满二叉树中编号从 1 到 n 的节点一一对应时,称为完全二叉树。
(3)二叉树的性质
-
性质① :二叉树的第 i 层上至多有 2i-1( i≥1 )个节点。
-
性质② :深度为 h 的二叉树中至多含有 2h-1 个节点。
-
性质③ :若在任意一棵二叉树中,有 n0 个叶子节点,有 n2 个度为 2 的节点,则必有 n0 = n2 + 1 。
-
性质④ :具有 n 个节点的满二叉树深为 log2n+1 。
-
性质⑤ :若对一棵有 n 个节点的完全二叉树进行顺序编号( 1≤i≤n ),那么,对于编号为 i( i≥1 )的节点: 当 i=1 时,该节点为根,它无双亲节点;当 i>1 时,该节点的双亲节点的编号为 i/2 ;若2i≤n ,则有编号为 2i 的左节点,否则没有左节点;若 2i+1≤n ,则有编号为 2i+1 的右节点,否则没有右节点。
二叉树的遍历
递归遍历
(1)先序遍历
先访问根节点,然后遍历左子树,最后遍历右子树。
(2)中序遍历
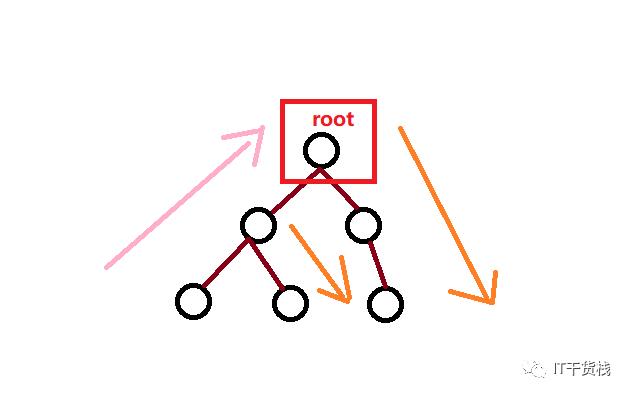
先遍历左子树,访问根结点,遍历右子树。
(3)后序遍历
先遍历左子树,再遍历右子树,最后访问根结点。
非递归遍历
(1)先序遍历
非递归方式遍历二叉树,需要引入额外的数据结构栈,其基本流程如下:
-
初始化一个栈,将根节点入栈。
-
当栈不为空时:
-
- 弹出栈顶元素 node ,将该节点值加入结果数组中;
-
- 若 node 的右子树不为空,右子树入栈;
-
- 若 node 的左子树不为空,左子树入栈。
(2)中序遍历
-
初始化一个空栈。
-
当根结点不为空或栈不为空时,从根节点开始:
-
- 若当前节点有左子树,一直遍历左子树,每次将当前节点压入栈中;
-
- 若当前节点无左子树,从栈中弹出该节点,尝试访问该节点的右子树。
(3)后序遍历
-
初始化一个空栈。
-
当根节点不为空或栈不为空时,从根节点开始:
-
- 每次将当前节点压入栈中,如果当前节点右左子树,就往左子树遍历,没有左子树就往右子树遍历。
-
- 若当前节点无左子树也无右子树,从栈中弹出该节点,如果当前节点是上一个节点(即弹出该结点后的栈顶元素)的左节点,尝试访问上个节点的右子树,如果不是,那当前栈的栈顶元素继续弹出。
层次遍历
二叉树的层次遍历,是指从二叉树的第一层(根结点开始)自上而下逐层遍历,同层内按照从左至右的顺序逐个节点访问。
-
首先根节点入队,当队列非空时,重复如下两步操作。
-
- 对头节点出队,并访问出对结点;
-
- 出队节点的左、右孩子依次入队。
遍历的实现
递归遍历的实现
(1)在任意目录下创建项目,编写一个名为 recursion.go 的程序实现二叉树的递归遍历,该程序的具体代码如下所示。
package Recursion
import (
"fmt"
)
type BinaryTreeNode struct
Value interface
Lchild *BinaryTreeNode
Rchild *BinaryTreeNode
func NewBinaryTreeNode(v interface) *BinaryTreeNode
return &BinaryTreeNodeValue: v
type Operate interface
// 打印结点的值
PrintValue()
// 递归先序遍历
PreOrder()
// 递归中序遍历
InOrder()
// 递归后序遍历
PostOrder()
func (b *BinaryTreeNode) PrintValue()
fmt.Printf(" %d ", b.Value)
func (b *BinaryTreeNode) PreOrder()
if b == nil
return
else
// 递归访问根节点
b.PrintValue()
// 递归访问左子树
b.Lchild.PreOrder()
// 递归访问右子树
b.Rchild.PreOrder()
func (b *BinaryTreeNode) InOrder()
if b == nil
return
else
// 递归访问左子树
b.Lchild.InOrder()
// 递归访问根节点
b.PrintValue()
// 递归访问右子树
b.Rchild.InOrder()
func (b *BinaryTreeNode) PostOrder()
if b == nil
return
else
// 递归访问左子树
b.Lchild.PostOrder()
// 递归访问右子树
b.Rchild.PostOrder()
// 递归访问根节点
b.PrintValue()
(2)在项目目录下编写一个名为 recursion_test.go 的程序测试以上遍历逻辑是否正确,该程序的具体代码如下所示。
package Recursion
import (
"fmt"
"testing"
)
func TestRangeBinaryTree(t *testing.T)
var bt Operate
root := NewBinaryTreeNode(5)
root.Lchild = NewBinaryTreeNode(3)
root.Rchild = NewBinaryTreeNode(1)
root.Lchild.Lchild = NewBinaryTreeNode(9)
root.Rchild.Rchild = NewBinaryTreeNode(6)
bt = root
fmt.Println("二叉树递归先序遍历:")
bt.PreOrder()
fmt.Println()
fmt.Println("二叉树递归中序遍历:")
bt.InOrder()
fmt.Println()
fmt.Println("二叉树递归后序遍历:")
bt.PostOrder()
fmt.Println()
(3)在该项目目录下执行 go test 命令,程序运行的结果如下所示。
二叉树递归先序遍历:
5 3 9 1 6
二叉树递归中序遍历:
9 3 5 1 6
二叉树递归后序遍历:
9 3 6 1 5
PASS
ok
非递归遍历的实现
(1)在任意目录下创建项目,编写一个名为 notrecursion.go 的程序实现二叉树的递归遍历,该程序的具体代码如下所示。
package NotRecursion
import (
"fmt"
)
type BinaryTreeNode struct
Value interface
Lchild *BinaryTreeNode
Rchild *BinaryTreeNode
func NewBinaryTreeNode(v interface) *BinaryTreeNode
return &BinaryTreeNodeValue: v
type Operate interface
// 打印结点的值
PrintValue()
// 非递归先序遍历
ReCallPreOrder()
// 非递归中序遍历
ReCallInOrder()
// 非递归后序遍历
ReCallPostOrder()
func (b *BinaryTreeNode) PrintValue()
fmt.Printf(" %d ", b.Value)
func (b *BinaryTreeNode) ReCallPreOrder()
St := make([]*BinaryTreeNode, 20)
top := -1
// 根结点非空,根节点进栈
if b != nil
top++
St[top] = b
// 栈非空时循环
for top > -1
// 退栈并访问该节点
p := St[top]
top--
fmt.Printf(" %d ", p.Value)
// 存在右孩子,将其进栈
if p.Rchild != nil
top++
St[top] = p.Rchild
// 存在左孩子,将其进栈
if p.Lchild != nil
top++
St[top] = p.Lchild
fmt.Println()
func (b *BinaryTreeNode) ReCallInOrder()
St := make([]*BinaryTreeNode, 20)
top := -1
if b != nil
p := b
// 根结点非空或栈非空时循环
for top > -1 || p != nil
// 扫描节点 p 的所有左下节点并进栈
for p != nil
top++
St[top] = p
p = p.Lchild
if top > -1
// 出栈节点 p 并访问
p = St[top]
top--
fmt.Printf(" %d ", p.Value)
p = p.Rchild
fmt.Println()
func (b *BinaryTreeNode) ReCallPostOrder()
St := make([]*BinaryTreeNode, 20)
top := -1
p := new(BinaryTreeNode)
var flag bool
// 根结点非空时循环
if b != nil
for
for b != nil
// 将 b 结点的所有左下结点进栈
top++
St[top] = b
b = b.Lchild
// p 指向当前节点的前一个已经访问过的节点
p = nil
// flag 为 true 时,表示正在处理栈顶节点
flag = true
for top != -1 && flag
// 取出当前的栈顶元素
b = St[top]
// 若右子树不存在或已被访问,访问 b 节点
if b.Rchild == p
fmt.Printf(" %d ", b.Value)
top--
// p 指向被访问的节点
p = b
else
// b 指向右子树
b = b.Rchild
// flag 为 false 时,表明当前不是处理的栈顶节点
flag = false
if top == -1
break
fmt.Println()
(2)在项目目录下编写一个名为 notrecursion_test.go 的程序测试以上遍历逻辑是否正确,该程序的具体代码如下所示。
package NotRecursion
import (
"fmt"
"testing"
)
func TestRangeBinaryTree(t *testing.T)
var bt Operate
root := NewBinaryTreeNode(5)
root.Lchild = NewBinaryTreeNode(3)
root.Rchild = NewBinaryTreeNode(1)
root.Lchild.Lchild = NewBinaryTreeNode(9)
root.Rchild.Rchild = NewBinaryTreeNode(6)
bt = root
fmt.Println("二叉树非递归先序遍历:")
bt.ReCallPreOrder()
fmt.Println("二叉树非递归中序遍历:")
bt.ReCallInOrder()
fmt.Println("二叉树非递归后序遍历:")
bt.ReCallPostOrder()
(3)在该项目目录下执行 go test 命令,程序运行的结果如下所示。
二叉树非递归先序遍历:
5 3 9 1 6
二叉树非递归中序遍历:
9 3 5 1 6
二叉树非递归后序遍历:
9 3 6 1 5
PASS
ok
层次遍历的实现
(1)在任意目录下创建项目,编写一个名为 travlevel.go 的程序实现二叉树的递归遍历,该程序的具体代码如下所示。
package TravLevel
import (
"fmt"
)
type BinaryTreeNode struct
Value interface
Lchild *BinaryTreeNode
Rchild *BinaryTreeNode
func NewBinaryTreeNode(v interface) *BinaryTreeNode
return &BinaryTreeNodeValue: v
type Operate interface
PrintValue()
TravLevel()
func (b *BinaryTreeNode) PrintValue()
fmt.Printf(" %d ", b.Value)
func (b *BinaryTreeNode) TravLevel()
// 定义环形队列
const MaxSize = 20
var Queue [MaxSize]*BinaryTreeNode
// 定义对首和队尾指针并置队列为空
front, rear := 0, 0
if b != nil
fmt.Printf(" %d ", b.Value)
// 根节点不为空进队
rear++
Queue[rear] = b
// 队列不为空时循环
for front != rear
// 出队节点 b
front = (front + 1) % MaxSize
b = Queue[front]
if b.Lchild != nil
// 输出左孩子并进队
fmt.Printf(" %d ", b.Lchild.Value)
rear = (rear + 1) % MaxSize
Queue[rear] = b.Lchild
if b.Rchild != nil
// 输出右孩子并进队
fmt.Printf(" %d ", b.Rchild.Value)
rear = (rear + 1) % MaxSize
Queue[rear] = b.Rchild
fmt.Println()
(2)在项目目录下编写一个名为 travlevel_test.go 的程序测试以上遍历逻辑是否正确,该程序的具体代码如下所示。
package TravLevel
import (
"fmt"
"testing"
)
func TestRangeBinaryTree(t *testing.T)
var bt Operate
root := NewBinaryTreeNode(5)
root.Lchild = NewBinaryTreeNode(3)
root.Rchild = NewBinaryTreeNode(1)
root.Lchild.Lchild = NewBinaryTreeNode(9)
root.Rchild.Rchild = NewBinaryTreeNode(6)
bt = root
fmt.Println("二叉树层次遍历:")
bt.TravLevel()
(3)在该项目目录下执行 go test 命令,程序运行的结果如下所示。
二叉树递归先序遍历:
5 3 9 1 6
二叉树递归中序遍历:
9 3 5 1 6
二叉树递归后序遍历:
9 3 6 1 5
PASS
ok
-
参考书籍:《数据结构教程 第6版》(李春葆 主编)
-
参考书籍:《数据结构 C语言版》(严蔚敏、李冬梅、吴伟民著)
go语言浅析二叉树

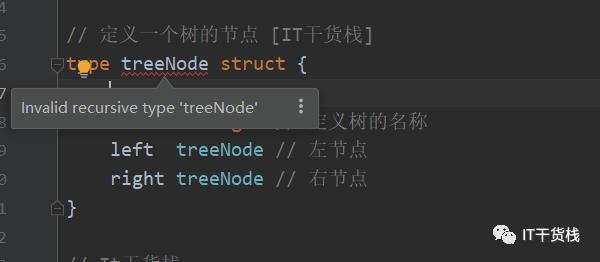
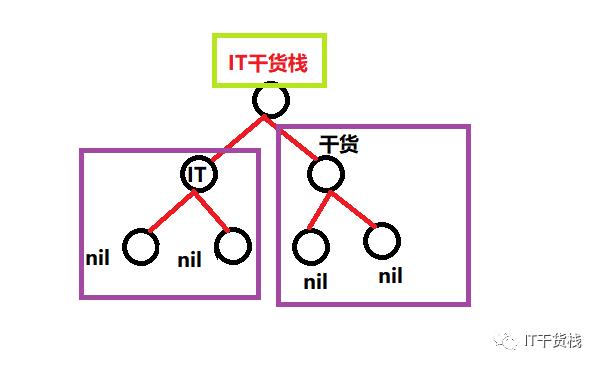
// 定义一个树的节点 [IT干货栈]type treeNode struct {name string // 定义树的名称left *treeNode // 左节点right *treeNode // 右节点}// It干货栈func main() {var node = treeNode{name: "It干货栈",left: &treeNode{name: "It",left: nil},right: &treeNode{name: "干货"}}addLeftNode(&node, 2)addLeftNode(node.left, 3)addLeftNode(node.left.left, 4)addLeftNode(node.left.left.left, 5)node.addRightNode(2)node.right.addRightNode(3)node.right.right.addRightNode(4)node.right.right.right.addRightNode(5)fmt.Println(node)}// 增加二叉树左节点func addLeftNode(node *treeNode, value int) {children := treeNode{name: fmt.Sprintf("子节点%s%d", "It干货栈", value)}node.left = &children} // 增加二叉树右节点func (node *treeNode)addRightNode(value int) {children := treeNode{name: fmt.Sprint("关注公众号", value),left: nil,right: nil,}node.right = &children}
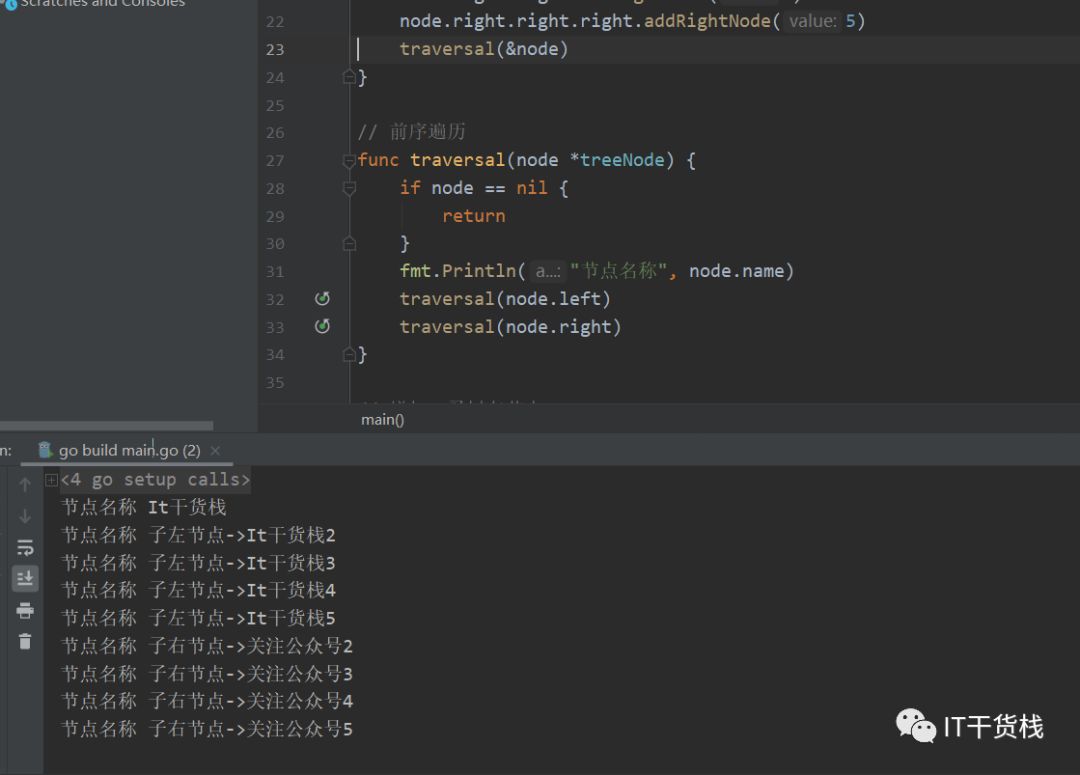
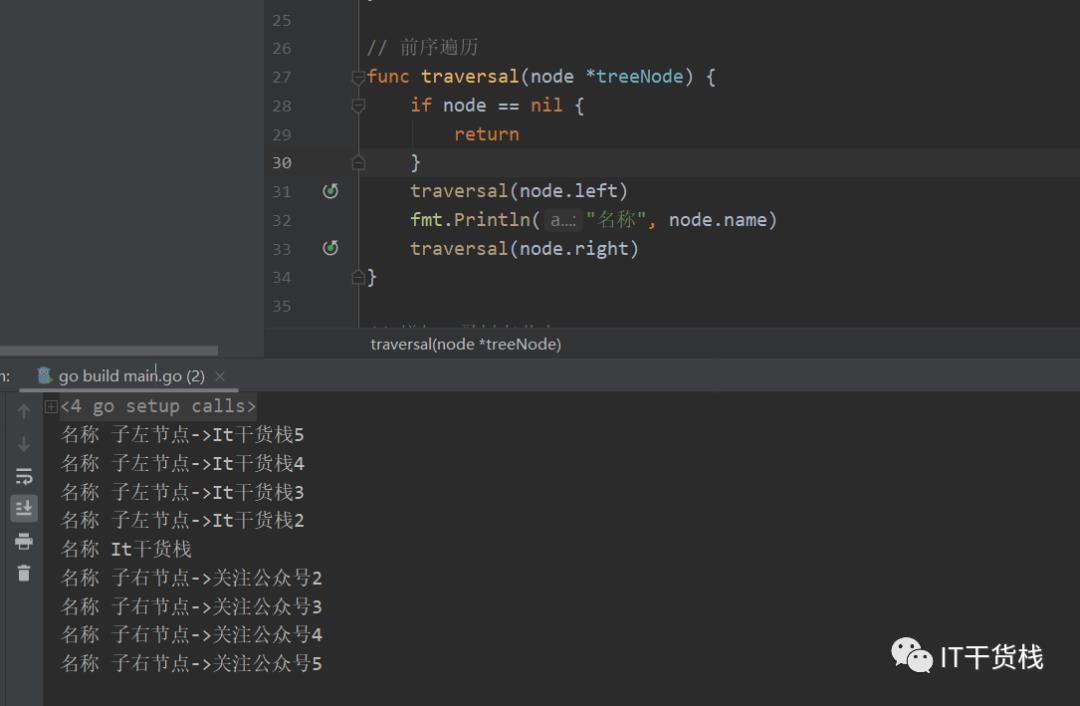
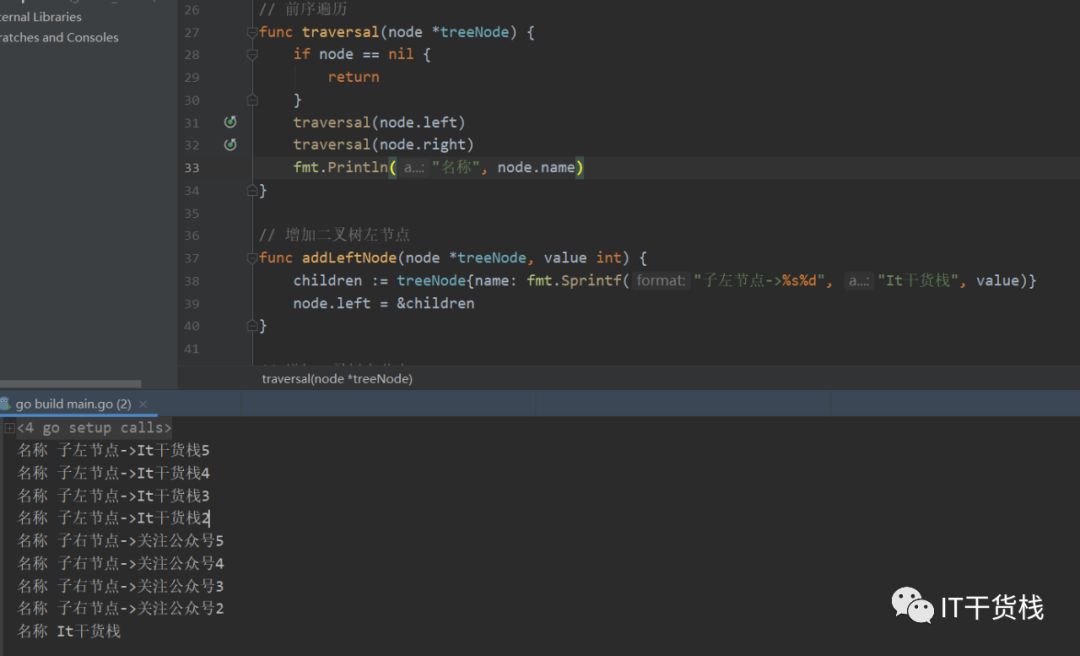
// 定义一个树的节点 [IT干货栈]type treeNode struct {name string // 定义树的名称left *treeNode // 左节点right *treeNode // 右节点}// It干货栈func main() {var node = treeNode{name: "It干货栈", left: &treeNode{name: "It", left: nil}, right: &treeNode{name: "干货"}}addLeftNode(&node, 2)addLeftNode(node.left, 3)addLeftNode(node.left.left, 4)addLeftNode(node.left.left.left, 5)node.addRightNode(2)node.right.addRightNode(3)node.right.right.addRightNode(4)node.right.right.right.addRightNode(5)traversal(&node)}// 遍历func traversal(node *treeNode) {if node == nil {return}traversal(node.left)traversal(node.right)fmt.Println("名称", node.name)}// 增加二叉树左节点func addLeftNode(node *treeNode, value int) {children := treeNode{name: fmt.Sprintf("子左节点->%s%d", "It干货栈", value)}node.left = &children}// 增加二叉树右节点func (node *treeNode) addRightNode(value int) {children := treeNode{name: fmt.Sprint("子右节点->关注公众号", value),left: nil,right: nil,}node.right = &children}
好了,今天的分享就到这啦,如果你喜欢我的分享,麻烦你点击一个好看或赞,我是小栈君,不定期分享IT干货,包括但不限于区块链、大数据、Python、go、等系列专题。原创不易,更新较慢,多多包涵。希望与你共同成长。我们下期再见啦,拜了个拜~
以上是关于数据结构之Go实现遍历二叉树的主要内容,如果未能解决你的问题,请参考以下文章