量化择时——SVM机器学习量化择时(第1部分—因子测算)
Posted 呆萌的代Ma
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了量化择时——SVM机器学习量化择时(第1部分—因子测算)相关的知识,希望对你有一定的参考价值。
文章目录
最近ChatGPT比较火,NLP的同学们感触肯定会更深。NLP的应用为人所知并积极部署是一件好事,但是应用层面上的每个应用场景都是过去的领域内SOTA模型不断攻克的任务。但是可惜的是,近年来,解决单一任务在算法层面的突破明显减速,应用层面却在加速推广。
ps:目前资讯里还没有见到提到“天网”这个词,hhhhhhh,当年VR,AR啥啥都没有的时候,漫山遍野的提“天网”要来啦,不知道这次的爆点又是什么
这里我们使用一个较为简单且常用的机器学习模型SVM,对择时提供帮助,以获得超额回报

机器学习在量化模型上的应用
机器学习量化应用场景
博主总结的机器学习应用与量化策略有以下三种场景:
- 构造胜率大于50的量化策略,无论模型是否可解释,通过增加交易次数,使综合收益向均线附近偏移,获取预期超额回报
- 在一个可能获取超额回报的逻辑框架上,使用机器学习模型优化细节,使预期收益均值在模型的加持下,向更高的回报偏移
- 以定价模型为基础,赚取修正市场的超额收益
而每一种场景都对应了不同的量化思路,同时也对应了不同的研究人员的知识体系:
- 第一种适合专业度足够高的工科背景,难点在于“历史不会重演”的前提下,论证模型可以获取超额回报,且获取超额回报也是大概率事件,以高频交易为主
- 第二种适合有编程能力的金融人员,难点在于论证可以取得超额回报的逻辑链条
- 第三种适合有编程能力,且富有经验的金融人员,难点在于识别并排除市场的噪声信息,或是对定价模型的修正与优化
量化模型有效性的思考
目前的共识是:投资任务的复杂性远远超出了机器学习能够处理的范围,因此通常需要在人为的框定一个逻辑框架内,用机器学习的模型来优化。
学习到现在,看了很多量化方面的书籍与策略,博主有些思考想和大家分享一下:
- 其实有很多同学和博主一样是计算机大类转到金融的,所以“量化”是我们一个不错的切入点,越偏向数据分析,也越是我们的舒适圈。但是人与算法相比:
- 人的优点是:剥离噪声,总结归纳,能把书越读越少
- 机器的优点是:统计、推理,能把书越读越厚
发展了半个多世纪的计量经济学模型已经说明金融、定价这些“结果数据”,它们的信息构成是混沌且带有随机性的,因此,在出策略的时候,最好不要让机器“替代自己思考”,算法的结果最多只能给与一些启发,远达不到辅助思考的程度。同时也不要“特征多多益善”,垃圾特征就是噪声源,而机器是无法自己筛选的,所以首先要“人”是懂金融有逻辑的,然后“人”去构造算法。
- 除了调参外,提升机器学习模型的效果一般有两种:
- 人为构造经得起逻辑推敲的特征序列
- 不要预先按照数据分析的固有规则剔除特征
经验哈,比如博主常用的随机森林模型,在不做调参的情况下,想要只通过调整特征与数据提升效果时,首先,不要根据有偏分布什么的,把这个特征剔除。因为每一个特征都是一个视角,有的视角比较准确,但是有的视角思路清奇。但是每个视角都是有价值的,这时我们需要人为的参与,构造一些合适的视角来配合这些特征,对特征做再次的加工。越是没有重要性的特征,越是灵感的来源,提升的空间也越大!而预先剔除掉就亏大了。
- 专业知识的不同会让我们看待世界的视角也不一样,正所谓“凡有所学,皆成性格”。金融专业的同学会把“风险管理”放在首要位置,同时对“幸存者偏差”事件有着近乎本能的辨识度,非常厉害!但据我观察很多量化策略为了追求“理论的均值”,会唯数据论,放纵模型发挥,这一点需要格外注意。
这篇博客只使用SVM模型测算,更多机器学习模型请参考:https://blog.csdn.net/weixin_35757704/article/details/89280669
机器学习模型在量化择时中的应用
训练与预测流程
使用机器学习通常有以下几个步骤:
- 数据清洗
- 切分训练集、测试集
- 使用训练集,交叉验证模型的稳定性
- 测试集判断模型的有效性
- 应用模型测算、回测
因此我们将时间切分成以下两个部分:
- 训练、测试数据时间:2015-01-01到2020-01-01
- 应用模型测算、回测时间:2020-01-01到2023-01-01
训练数据特征构造
这里我们构造的特征简单一些,以方便大家复现:
- 过去5日换手率均值
- 过去10日换手率均值
- 过去5日涨跌幅
- 过去10日涨跌幅
- MACD指标DIF值
- MACD指标DEA值
- MACD值
- 阿隆指标(一种动量指标)DOWN值
- 阿隆指标UP值
SVM模型与测算
SVM训练与预测
通常,拿到数据后,以最终收益为目标的模型,主要有以下几种训练目标:
- 直接预测未来一段时间的收益率
- 预测未来一段时间的收益所处的区间
机器学习模型由于性能有限,通常以收益率为最终目标时,会选择“预测未来一段时间的收益所处的区间”
因此我们按照以下规则进行训练、预测:
- 70%的数据做训练集,30%的数据做测试集
- 将【未来5日涨跌幅】作为预测目标,同时将数据分箱,分为:
- 收益率区间:[负无穷,-1]
- 收益率区间:[-1,1]
- 收益率区间:[1,正无穷]
- 训练集中,做10次交叉验证
- 测试集计算混淆矩阵,并可视化
上面的“交叉验证”是为了判断过拟合与欠拟合的问题的,很多文章容易把效果差的锅甩给“过拟合”,但明显是有问题的。关于过拟合与欠拟合请参考:https://blog.csdn.net/weixin_35757704/article/details/123931046
效果测算
测算的流程如下:
- 收集每一个非ST的股票在2015-01-01到2020-01-01的时间
- 然后根据个股的股价走势,构造成上面9个特征
- 按照70%的数据做训练集,30%的数据做测试集
- 对训练集做10份交叉验证
按照如上规则进行训练与预测,得到如下模型结果:
-
按照上述测算流程进行测算,在测试集上的准确率为 0.4751
-
归一化后的混淆矩阵如下:
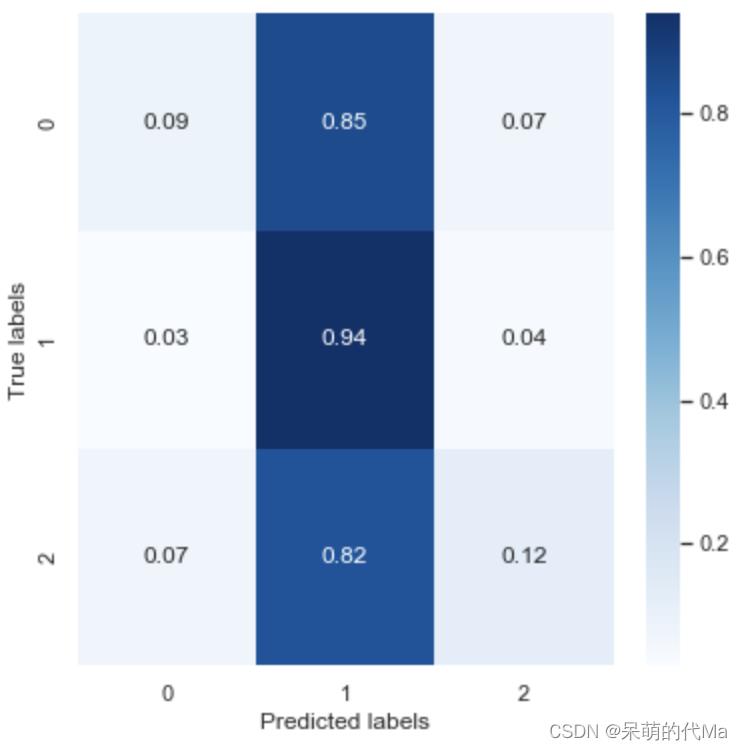
-
使用10份交叉验证的结果如下:
| 准确率效果 | 0.492502 | 0.488092 | 0.478529 | 0.473529 | 0.485882 | 0.477647 | 0.477059 | 0.484118 | 0.480882 | 0.486176 |
|---|
在实际使用时,我们会根据模型的逻辑效果来判断:如果模型预测为正收益,则买入;如果预测为负收益,则卖出;
效果分析
- 交叉验证的效果与测试集的预测效果差不多,说明SVM模型表现较为稳定
- SVM将0,1,2等类别几乎无差别的预测为了类别1,抛开本身类别为1的,单单计算0与2的准确率只有10%
这个效果算中规中矩,因为没有优化、调整、或者主观构造特征,裸模型的效果也就差不多这个效果…
Matlab量化投资支持向量机择时策略
推出【Matlab量化投资系列】
机器学习
所谓机器学习,其实就是根据样本数据寻找规律,然后再利用这些规律来预测未来的数据(结果)。
但是,直到今天,机器学习也没有一种被大家广泛认同的理论框架产生,这个也是机器学习被大家诟病的原因之一:它是没有理论基础的。
目前机器学习的方法大概可以分为以下几种:
1、经典的参数统计估计方法:基于传统统计学,需要已知的样本分布形式,局限性比较大。
2、经验非线性方法:利用已知样本建立非线性模型(如人工神经网络),克服了传统参数估计方法的困难,但缺乏统一的数学理论。
3、统计学习理论(SLT):专门研究小样本情况下机器学习规律的理论,核心概念是VC维概念,解决了神经网络结构选择、局部极小点等问题。支持向量机(SVM)就是基于这一理论产生的。
SVM支持向量机择时策略
支持向量机
支持向量机是用来解决分类问题的。
先考虑最简单的情况,豌豆和米粒,用晒子很快可以分开,小颗粒漏下去,大颗粒保留。用一个函数来表示就是当直径d大于某个值D,就判定为豌豆,小于某个值就是米粒。
d>D, 豌豆;d<D, 米粒
在数轴上表现为d左边就是米粒,右边就是绿豆,这是一维的情况。
但是实际问题没这么简单,考虑的问题不单单是尺寸。
一个花的两个品种,怎么分类?
假设决定他们分类的有两个属性,花瓣尺寸和颜色。单独用一个属性来分类,像刚才分米粒那样,就不行了。这个时候我们设置两个值:尺寸x和颜色y。
我们把所有的数据都丢到x-y平面上作为点,按道理如果只有这两个属性决定了两个品种,数据肯定会按两类聚集在这个二维平面上。
我们只要找到一条直线,把这两类划分开来,分类就很容易了,以后遇到一个数据,就丢进这个平面,看在直线的哪一边,就是哪一类。
例如:x+y-2=0这条直线,我们把数据(x,y)代入,只要认为x+y-2>0的就是A类,x+y-2<0的就是B类。
以此类推,还有三维的,四维的,N维的属性的分类,这样构造的也许就不是直线,而是平面,超平面。
例如:一个三维的函数分类 :x+y+z-2=0,这就是个分类的平面了。
有时候,分类的那条线不一定是直线,还有可能是曲线,我们通过某些函数来转换,就可以转化成刚才的那种多维的分类问题,这个就是核函数的思想。
例如:分类的函数是个圆形x^2+y^2-4=0。这个时候令x^2=a; y^2=b,还不就变成了a+b-4=0 这种直线问题了。
这就是支持向量机的思想。
机的意思就是算法,机器学习领域里面常常用“机”这个字表示算法。
支持向量意思就是数据集种的某些点,位置比较特殊,比如刚才提到的x+y-2=0这条直线,直线上面区域x+y-2>0的全是A类,下面的x+y-2<0的全是B类,我们找这条直线的时候,一般就看聚集在一起的两类数据,他们各自的最边缘位置的点,也就是最靠近划分直线的那几个点,而其他点对这条直线的最终位置的确定起不了作用,所以我姑且叫这些点叫“支持点”(意思就是有用的点),但是在数学上,没这种说法,数学里的点,又可以叫向量,比如二维点(x,y)就是二维向量,三维度的就是三维向量(x,y,z)。所以 “支持点”改叫“支持向量”,听起来比较专业,NB。
所以就是”支持向量机了。
当然了,SVM的实际理论要复杂的多,如果大家有兴趣,就自行去搜索一下参考资料来看啦,由于篇幅关系,这边就不赘述了。
核函数分类
目前应用最多的四类核函数分别为:线性核函数、多项式核函数、高斯核函数和Sigmoid核函数。
选择不同的核函数和参数,SVM的性能会有很大的差异,因此核函数及其参数的选择是SVM理论和应用研究中的一个重要课题。
SVM看上去是比较复杂,但是在实际应用当中还是比较简单的,因为Matlab本身就已经提供了SVM的工具箱(函数),我们直接调用就可以了,当然,大家也可以自行去安装一些其他SVM的工具箱来实现。
那下面我们就开始编写策略啦~
小编所使用的数据、策略回测、交易等等都是来自于国泰安量化终端Quantrader。而小编使用的策略编写语言是Matlab,实现策略不要太简单。
策略简介
订阅中证800指数和相应的成分股,使用了日频最高价、最低价、收益率、成交金额、营业收入增长率和次日停牌因子等数据。
策略流程图如下:
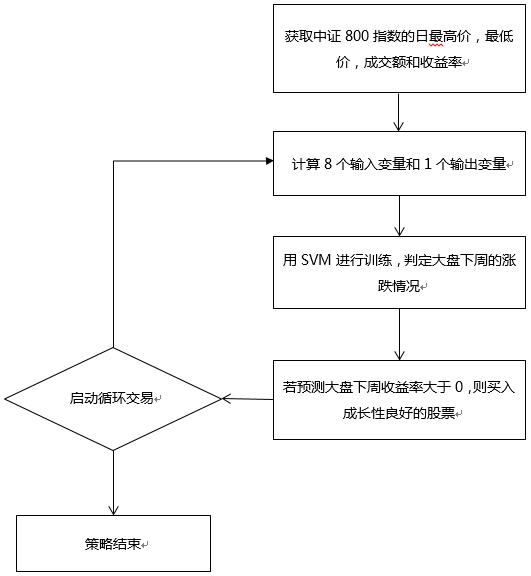
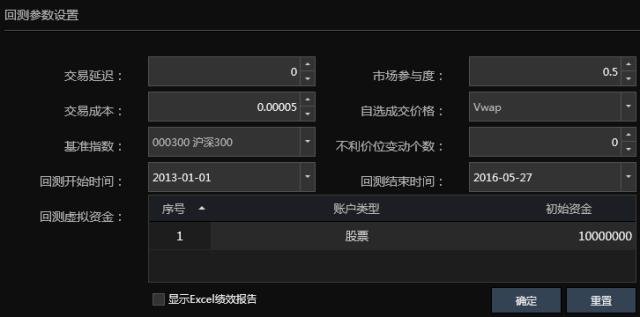
策略参数配置
根据之前提到的订阅的交易代码和数据,使用Quantrader可以直接配置如下:
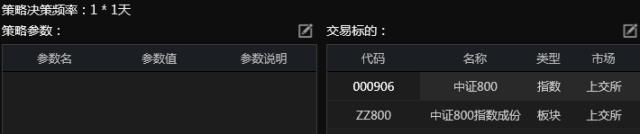
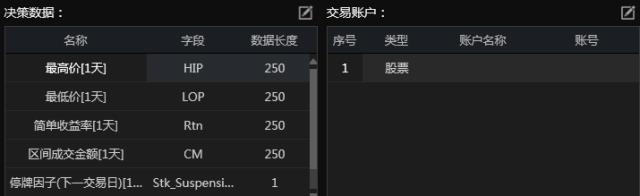
策略主程序
数据准备好了之后,我们就可以开始码代码啦。
1、训练分类器:

2、预测:

3、交易下单:

策略回测
策略写完了当然要用历史数据回测看看绩效。同样的,使用Quantrader,完成回测。
从过去3年半的绩效来看,这个策略年化收益约50%左右,夏普达到了2。
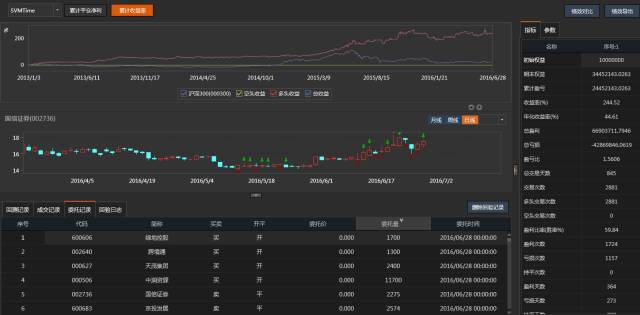
完整版源代码请点击阅读原文
关注者
从1到10000+
每天我们都在进步
阅读量前10文章
No.01
No.02
No.03
No.04
No.05
No.06
No.07
No.08
No.09
No.10
以上是关于量化择时——SVM机器学习量化择时(第1部分—因子测算)的主要内容,如果未能解决你的问题,请参考以下文章