动态规划-Python实现-四种规划全包括

Posted 2023-04-03 Mooan

题记

动态规划是蓝桥杯常考的题型，同时也是建模常考的规划。但是我翻了一些博客，我发现很少有用Python实现。所以，参照几篇博客进行总结和归纳后，我整理出来了全面的动态规划使用场景+代码。

动态规划是什么？

看一遍就理解：动态规划详解 - 云+社区 - 腾讯云 (tencent.com)

这位大佬写的真的通俗易懂，方便大家理解。文中涉及的代码转换成Python代码如下：

 线性规划的分类及代表问题

线性动规：拦截导弹，合唱队形，挖地雷，建学校，剑客决斗等；

区域动规：石子合并，加分二叉树，统计单词个数，炮兵布阵等；

树形动规：贪吃的九头龙，二分查找书，聚会的欢乐，数字三角形等；

背包问题：01背包问题，完全背包问题，分组背包问题，二维背包，装箱问题，挤牛奶等；

应用实例：最短路径问题，项目管理，网络流优化等。

 一、线性动归

 1.青蛙跳阶

青蛙跳阶-递归

def numWays(n):
    if n==1:
        return 1
    elif n==2:
        return 2
    else:
        return numWays(n-1)+numWays(n-2)
n=eval(input())
print(numWays(n)%1000000007)

青蛙跳阶-带备忘录的递归

lt=[1,2]
for i in range(2,n):
    lt.append(lt[i-1]+lt[i-2])
n=eval(input())
print(lt[n-1]%1000000007)

青蛙跳阶-自底向上的动态规划

a,b=1,2
n=eval(input())
for i in range(2,n):
    a,b=b,(a+b)%1000000007
print(b)

2.穷举分析

s=input()#输入格式x1,x2,x3,...
ls=list(map(int,s.split(',')))
n=len(ls)
dp=[1 for i in range(n)]
maxlen=1
for i in range(n):
    for j in range(0,i):
        if ls[i]>ls[j]:
            dp[i]=max(dp[i],dp[j]+1)
    maxlen=max(maxlen,dp[i])
print(maxlen)
print(dp)

结果： （和博客中分析结果一致）

 分析：这道题看起来真的挺难的，但是如果正确分析，就会发现其实这道题的代码很简单。所以这个题的解决思路要重点关注。

3.钢条切割

题目和分析见这篇博客的[动态规划小试牛刀]

算法-动态规划 Dynamic Programming--从菜鸟到老鸟_HankingHu的博客-CSDN博客_动态规划

钢条切割-递归

value=[0,1,5,8,9,10,17,17,20,24,30]
length=list(range(0,11))#定义价格和长度
def cutmax(n):
    if n<=0:
        return 0
    elif n==1:
        return 1
    else:
        q=value[n]
        for i in range(1,n):
            q=max(q,cutmax(i)+cutmax(n-i))
        return q
x=eval(input())
print(cutmax(x))

钢条切割-备忘录

这道题的备忘录方法没什么意思，备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。过程：定义函数-->循环调用函数+保存结果，代码太长太冗余了，直接学习动态规划方法吧。

钢条切割-自底向上的动态规划

value=[0,1,5,8,9,10,17,17,20,24,30]
x=eval(input())
valuemax=value.copy()
if x>10:
    valuemax+=[0]*(x-10)
for i in range(1,x+1):
    for j in range(1,i):
        valuemax[i]=max(valuemax[i],valuemax[j]+valuemax[i-j])
print(valuemax[x])

4.合唱队形问题

动态规划——合唱队 - Achilles_Heel - 博客园 (cnblogs.com)

这个博客也是用Python写的，我改进了一下。

问题补充：（我一开始的疑问）

问题分析中有这样的描述：（第i位同学被重复计算了一次），但是同样存在第i位同学不被重复计算的情况（如下图），这时-1就使合唱人数变小。但是我发现这时的升序人数+降序人数一定小于i取i-1或者i+1时：i=i+1时，升序=4，降序=3；i=i时，升序=3，降序=3。所以虽然当等于i时计算结果有误，但是不会影响最大值的选取。

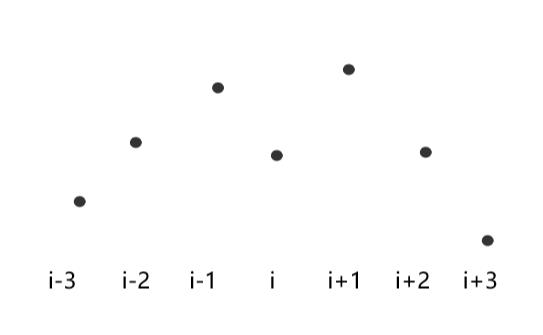
 在3.穷举分析的代码基础上写代码（对照答案结果一样）

s=input()#输入格式x1,x2,x3,...
ls=list(map(int,s.split(',')))
n=len(ls)
up=[1 for i in range(n)]
down=[1 for i in range(n)]
for i in range(n):
    for j in range(0,i):
        if ls[i]>ls[j]:
            up[i]=max(up[i],up[j]+1)
        if ls[n-i-1]>ls[n-j-1]:
            down[n-i-1]=max(down[n-i-1],down[n-j-1]+1)
maxlen=[]
for k in range(n):
    maxlen.append(n-(up[k]+down[k])+1)
print(min(maxlen))
print(up)
print(down)
print(maxlen)

 二、区域动归

1.石子合并

动态规划之合并石子_Zekary的博客-CSDN博客_石子合并问题c语言

解法非常清晰，代码转成Python代码如下。

目标方程：minCost [ i ] [ i + k - 1] = min(minCost[ i ][ j ] + minCost[j + 1][ i + k - 1] + theCost)来源【算法笔记】区域型动态规划_石子并归_小宋今天要早睡的博客-CSDN博客_区域动态规划

s=input() #输入格式x1,x2,x3,...
ls=list(map(int,s.split(',')))
n=len(ls)
summ=[]
for i in range(n):
    t=[]
    for j in range(n):
        if j<i:
            t.append(0)
        elif j==i:
            t.append(ls[i])
        else:
            t.append(t[j-1]+ls[j])
    summ.append(t)

dp=[[0 for i in range(n)] for j in range(n)]
for i in range(n):
    if i<n-1:
        dp[i][i+1]=ls[i]+ls[i+1]

for t in range(2,n+1):
    for i in range(n-t):
        a=dp[i][i+t-1]+summ[i][i+t]
        b=dp[i+1][i+t]+summ[i][i+t]
        for j in range(1,t-1):
            b=min(b,dp[i][i+j]+dp[i+j+1][i+t]+summ[i][i+t])
        dp[i][t+i]=min(a,b)
print(dp[0][n-1])

 2.加分二叉树

自从计算机二级开始我就对二叉树充满畏惧感，一开始碰到这道题也是完全不想看的状态，但是这种题还挺多的，之前碰到什么左孩子右兄弟也是完全不会做。。。所以这道题我要克服恐惧！

【题解】加分二叉树_Fool-Fish的博客-CSDN博客

这篇博客就是我的学习内容，内容很清晰，而且排版令人很舒服。

def p(L,r):
    if L>r:
        return
    print(root[L][r],end=' ')
    if L==r:
        return
    p(L,root[L][r]-1)
    p(root[L][r]+1,r)   #输出根节点函数
    
n=eval(input())
s=input()
a=[0]+list(map(int,s.split()))

dp=[[0 for i in range(n+1)] for j in range(n+1)]    #用来保存节点的得分
root=[[0 for i in range(n+1)] for j in range(n+1)]  #用来保存i,j的共同的根节点

for i in range(1,n+1):
    dp[i][i]=a[i]
    dp[i][i-1]=1
    root[i][i]=i  #构造初始的数据

for len in range(1,n):
    for L in range(1,n-len+1):
        r=L+len
        dp[L][r]=dp[L+1][r]+a[L]
        root[L][r]=L
        #print('len,L,r=',len,L,r)
        for k in range(L+1,r):
            if dp[L][r]<dp[L][k-1]*dp[k+1][r]+a[k]:
                dp[L][r]=dp[L][k-1]*dp[k+1][r]+a[k]  #取最大得分
                root[L][r]=k 

print(dp[1][n])
p(1,n)

结果：

 从图中可以看出来计算分数一步一步的过程，结果相同。代码在题库中测试，百分百通过。

 三、树形动态规划

1.贪吃的九头龙

【NOI2002】贪吃的九头龙_SSLGZ_yyc的博客-CSDN博客

【这里看起来比较难，待补充】【最近要期中考试了，之后再补】

四、背包问题

1. 01背包

01背包问题详解（浅显易懂）_Iseno_V的博客-CSDN博客_01背包问题详解

背包问题的小试牛刀，这个比较容易，讲的也很详细，懂了这个之后复杂的背包问题就比较容易懂了。

n=eval(input())
V=eval(input())
s1=input()  #w1,w2,w3,...
w=[0]+list(map(int,s1.split(',')))
s2=input()  #v1,v2,v3,...
v=[0]+list(map(int,s2.split(',')))

f=[0 for i in range(V+1)]
for i in range(1,n+1):
    for j in range(V,w[i]-1,-1):
        f[j]=max(f[j],f[j-w[i]]+v[i])

print(f[V])

2.背包九讲

dd大牛的《背包九讲》 - 知乎 (zhihu.com)

这个比较完整，讲解也比较详细易懂，也比较长，但是没有题目和代码。

背包九讲----整理+例题_smiling~的博客-CSDN博客_背包九讲

这个讲解不那么详细，但是最重要的dp方程都给出来了。如果前面的代码都跟着我一起学习过一遍了，思路也不需要讲的那么详细其实也可以明白了。所以这个也推荐看，但是代码是C++，后续陆续补充其中代码。【两个博客可以对照学习，代码可以来参照我的代码】

我直接用acwing的题库测试代码，通过的代码会放在这里。

注意一下，acwing网站里的Python编译器是Python2.x版本的，所以有些地方会莫名其妙报错，所以有些函数要稍微改一下。比如：input-->raw_input 

 1.01背包：acwing02 2. 01背包问题 - AcWing题库

n,V=map(int,raw_input().split(' '))
w=[0];v=[0]
for i in range(n):
    t1,t2=map(int,raw_input().split(' '))
    w.append(t1)
    v.append(t2)

f=[0 for i in range(V+1)]
for i in range(1,n+1):
    for j in range(V,w[i]-1,-1):
        f[j]=max(f[j],f[j-w[i]]+v[i])
    #print('i=',i,'\\t','f=',f)

print(f[V])

 

 输出一下结果可以清晰的看到往背包里加入物品的过程。

2. 完全背包：acwing03 3. 完全背包问题 - AcWing题库

n,V=map(int,raw_input().split())
w=[0];v=[0]
for i in range(n):
    t1,t2=map(int,raw_input().split())
    w.append(t1)
    v.append(t2)

f=[0 for i in range(V+1)]
for i in range(1,n+1):
    for j in range(w[i],V+1):
        f[j]=max(f[j],f[j-w[i]]+v[i])
    #print('i=',i,'\\t','f=',f)

print(f[V])

3.多重背包：

【先写到这，待补充】

动态规划算法入门练习 (python实现)

动态规划（英语：Dynamic programming，简称DP）是一种在数学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。在生物信息领域，比如在序列比对的时候，就用到了动态规划的思想。在隐马尔科夫模型中的维特比 (Viterbi) 算法也使用了动态规划算法。

  1.  爬楼梯 

【题目】有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。求出一共有多少种走法。

【思路】这个问题仔细想想其实与斐波那契数列很像，同样可用递归求解。

假如最后我们已经爬上了10层，那么最后一个步骤走了要么一步， 要么两步。也就是说，我们到10层的走法，其实就是我们走到八层和九层的方法的和。即F(n) = F(n-2) + F(n-1)。

【解法1】递归

def climb(n):
    if n == 1:
        return 1
    elif n == 2:
        return 2
    else:
        return climb(n - 1) + climb(n - 2)

climb(10)

【解法2】动态规划

def climb(n):
    way = [0] * n
    way[0] = 1
    way[1] = 2
    for i in range(2, n):
        way[i] = way[i - 1] + way[i - 2]
    return way[n - 1]

# 或者
def climb=(n):
    if n <= 2:
        return n
    else:
        a, b = 1, 2
        for i in range(n - 2):
            a, b = b, a + b
        return b

climb(10)

 2.  打家劫舍 

【题目】你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

【例子】

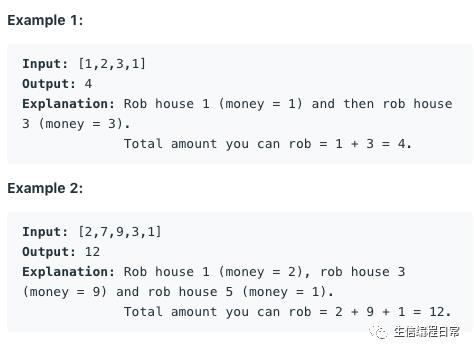
【思路】当我们偷窃到第i家的时候，所能偷到的就是一直到第i - 1家所偷到的与第i - 2家和第i家偷到的钱的和的最大值，即dp[i] = max(nums[i] + dp[i -2], dp[i-1])。 

【解法1】

def rob(nums):
    size = len(nums)
    
    if size == 1:
        return nums[0]
    elif size == 2:
        return max(nums[0], nums[1])
    elif size == 0:
        return 0     
    else:
        dp = [0] * size
        dp[0], dp[1] = nums[0], max(nums[0], nums[1])

        for i in range(2, size):
            dp[i] = max(nums[i] + dp[i - 2], dp[i - 1])

        return dp[-1]

【解法2】优化 只用到了dp[i-2]与dp[i-1]的值，不需要列表

def rob(nums):
    now = last = 0
    for i in range(len(nums)):
        now, last = max(last + nums[i], now), now
    return now

3.  除数博弈

【题目】爱丽丝和鲍勃一起玩游戏，他们轮流行动。爱丽丝先手开局。

最初，黑板上有一个数字 N 。在每个玩家的回合，玩家需要执行以下操作：

选出任一 x，满足 0 < x < N 且 N % x == 0 。

用 N - x 替换黑板上的数字 N 。

如果玩家无法执行这些操作，就会输掉游戏。

只有在爱丽丝在游戏中取得胜利时才返回 True，否则返回 false。假设两个玩家都以最佳状态参与游戏。

【例子】

【思路1】动态规划

可以分析一步步地先分析一下，找一下其中规律：

当N = 1时，Alice没有选择，输；

当N = 2时，Alice选1，Bob没有选择， 赢。

当N = 3时，Alice选1，Bob选的时候N=2，根据上一个结果，先手赢，所以Bob赢，Alice输。

当N = 4时，Alice选1，Bob选的时候N=3，根据上一个结果，先手输，Bob会输，Alice赢。

……

以此类推，可以看出，假如alice选的k，那么N%k==0和当N-k的时候必须输（即Bob的时候必输）这两个条件必须满足。

【解法1】

def divisorgame(N):
    if N <= 1:
        return False
    else:
        dp = [False] * N
        dp[0] = False
        dp[1] = True

        for i in range(3, N + 1): # N的实际取值
            for j in range(1, i // 2 + 1):
                if i % j == 0 and dp[i-1-j] == False:
                    dp[i-1] = True
                    break
        return dp[-1]

【思路2】数学归纳

上面的动态归纳法需要两层循环，效率较低，仔细分析一下这个题，还有额外的解法。看一下结果，可以发现，当N为奇数时，Alice（先手）必输；当N为偶数时，Alice必赢。因为：

• 最后一步中，拿到2的一定会赢，拿到1的会输。

• 当N为奇数时，其约数一定是奇数，所以Bob拿到的一定会是偶数，Bob拿1，这样Alice拿到的还是奇数，这样一直到Bob拿到2，Alice就会输掉。

• 当N为偶数时，偶数的约数可奇可偶，Alice可以选1或者一个奇数，Bob拿到的就是一个奇数，从上面可知奇数必输。Alice则会赢。

所以此题就会转化为一个数学问题。

【解法2】

def divisorgame(N):
    return N % 2 == 0