AtCoder Beginner Contest 296 G.Polygon and Points(计算几何/凸包上二分)

Posted 2023-04-02 Code92007

题目

给一个n(n<=2e5)个点的凸包（显然无三点共线），点序按逆时针序给出

q(q<=2e5)个询问，第i次询问点(xi,yi)是否在凸包内/外/上，

在凸包上输出ON，在凸包内输出IN，在凸包外输出OUT

对于所有点(x,y)，每一维在[-1e9,1e9]之间

思路来源

https://www.cnblogs.com/Felix-F/p/3249568.html

SGU 253 log（n）判点在凸包内 二分_9974的博客-CSDN博客

题解

十年前的老题sgu253了，被abc296又翻出来了

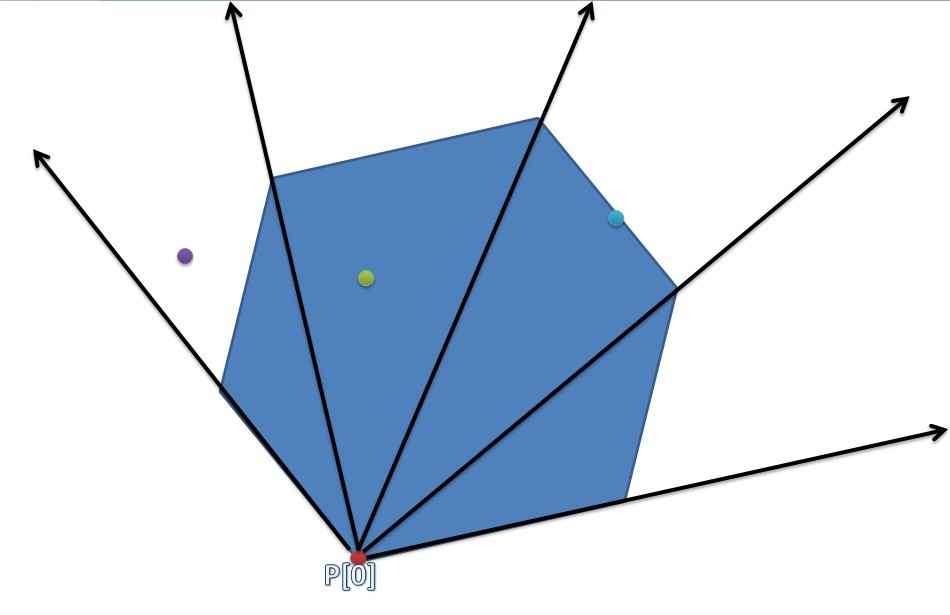
如图，逆时针序，p[0]和每个点连一条射线，将凸包划分为若干个三角形

二分询问点是否在其中某个三角形内，具体来说，

将逆时针每个点依次标号0到n-1，

初始令l=0，r=n-1（实际不会取到r），二分到m时，

计p[0]p[m]为右射线，p[0]p[m+1]为左射线，p[m]p[m+1]为上射线，

在某个三角形内部或在三角形上，当且仅当：

①点tp，即向量p[0]tp，在右射线逆时针方向

②点tp，即向量p[0]tp，在左射线顺时针方向

③点tp，即向量p[m]tp，在上射线逆时针方向

分别叉积判断即可，

若①满足，说明在逆时针方向，往l更大二分，

否则，往r更小二分

IN的情形，对应在三角形内部；

ON的情形，只可能是在上射线上，或者p[0]p[1]上，或者p[0]p[n-1]上

其余都是OUT的情形

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
struct Point
    int x,y;
p[N];
int n,m;
ll cross(Point o,Point a,Point b)
    return 1ll*(a.x-o.x)*(b.y-o.y)-1ll*(a.y-o.y)*(b.x-o.x);

int binary(Point *p,Point &tp)
    //条件：p点集必须是顺时针或者逆时针
    //（注意3点共线下的点也必须满足这个条件）
    //（如果有3点共线极角序不能完成该条件）
    int l=0,r=n-1;
    while(l<r)
        int m=(l+r)>>1;
        ll c1=cross(p[0],p[m],tp);
        ll c2=cross(p[0],p[(m+1)%n],tp);
        ll c3=cross(p[m],p[(m+1)%n],tp);
        if(c1>=0 && c2<=0 && c3>=0)
            if(!c3 || (m==1 && !c1) || (m==n-2 && !c2))return 0;
            return 1;
        
        if(c1>=0)l=m+1;
        else r=m;
    
    return -1;

int main()
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    
    scanf("%d",&m);
    p[n]=p[0];
    while(m--)
        Point tp;
        scanf("%d%d",&tp.x,&tp.y);
        int v=binary(p,tp);
        if(v==1)puts("IN");
        else if(v==0)puts("ON");
        else puts("OUT");
    
    return 0;

Atcoder Beginner Contest 251 D——题解

纯文本提交，居然还能AC？

纯文本提交，居然还能AC？