python进行敏感性分析（SALib库)

Posted 2023-04-02 bujbujbiu

什么是敏感性分析

敏感性分析（sensitivity analysis）是指从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。每个输入的灵敏度用某个数值表示即敏感性指数（sensitivity index）
敏感性指数包括以下几种：

• 一阶指数：度量单个模型输入对输出方差的贡献
• 二阶指数：度量两个模型输入的相互作用对输出方差的贡献
• 总阶指数：度量模型输入对输出方差的贡献，包括一阶及更高阶

什么是SALib

SALib是一个基于python进行敏感性分析的开源库，SALib提供一个解耦的工作流，意味着它不直接与数学或计算模型交互，SALib 负责使用其中一个采样函数（sample functions）生成模型输入，并使用其中一个分析函数（analyze functions）计算模型输出的灵敏度指数。使用 SALib 进行敏感性分析遵循四个步骤：

• 确定模型输入（参数）及采样范围
• 运行采样函数生成模型输入
• 使用生成的输入评估模型，保存模型输出
• 基于模型输出运行分析函数计算敏感性指数
  SALib提供了几种灵敏度分析函数，如Sobol，Morris和FAST。有许多因素决定了哪种方法适用于特定应用。但是无论选择哪种方法，都只需要用到两种函数：sample，analyze

案例1

对Ishigami function进行Sobol敏感性分析，因为Ishigami函数表现出很强的非线性和非单调性，所以常用来测试不确定性和敏感性分析方法

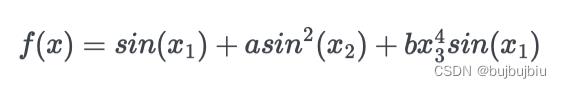
1.导入库

SALib的采样和分析存储在不同的模块中，例如导入saltelli采样函数和sobol分析函数，使用Ishigami作为测试函数，numpy用于存储模型输入和输出

from SALib.sample import saltelli
from SALib.analyze import sobol
from SALib.test_functions import Ishigami
import numpy as np

2.定义模型输入

Ishigami函数有三个输入：$x_1$,$x_2$,$x_3$。每个变量取值[$\pi$,$-\pi$]。定义一个参数的字典包括输入数量，输入名称，每个输入的边界

problem = 
    'num_vars':3,
    'names':['x1','x2','x3'],
    'bounds':[[-3.14159265359, 3.14159265359],
              [-3.14159265359, 3.14159265359],
              [-3.14159265359, 3.14159265359]]

3.生成样本

使用saltelli生成样本

param_values = saltelli.sample(problem,1024)

param_values是一个numpy矩阵，其大小为(8192, 3)，saltelli会生成N*(2D+2)个样本，其中N=1024（传入参数），D=3（模型输入数量）。参数calc_second_order=False表示不包括二阶指数，采样数变为N*(D+2)

param_values

array([[-3.13238877, -0.77619428, -0.32827189],
       [-0.08283496, -0.77619428, -0.32827189],
       [-3.13238877,  0.3589515 , -0.32827189],
       ...,
       [-0.93572828,  0.80073797,  0.99095159],
       [-0.93572828,  0.81914574,  2.70901007],
       [-0.93572828,  0.81914574,  0.99095159]])

param_values.shape

(8192, 3)

4.运行模型

SALib不直接参与数学或计算模型的评估，如果模型是用python书写，可以直接循环遍历每个样本输入和评估模型

Y = np.zeros([param_values.shape[0]])
for i,X in enumerate(param_values):
    Y[i] = evaluate_model(X)

如果模型不是python书写，可以保存模型的输入输出

np.savetext('param_values.txt',param_values)
Y = np.loadtxt('outputs.txt',float)

本例中使用Ishigami函数评估样本数据

Y = Ishigami.evaluate(param_values)
Y

array([ 3.426362  ,  3.3527401 ,  0.85463176, ...,  2.72470174,
       -1.40463805,  2.85339365])

5.分析

在得到模型的输出后可以计算敏感性指数。本例中使用sobol.analyze，会计算一阶，二阶和总阶指数

Si = sobol.analyze(problem,Y,print_to_console=True)

          ST   ST_conf
x1  0.555860  0.080045
x2  0.441898  0.034177
x3  0.244675  0.025569
          S1   S1_conf
x1  0.316832  0.068707
x2  0.443763  0.046636
x3  0.012203  0.064176
                S2   S2_con
(x1, x2)  0.009254  0.093058
(x1, x3)  0.238172  0.111655
(x2, x3) -0.004888  0.066105

Si是一个字典，关键词有"S1", “S2”, “ST”, “S1_conf”, “S2_conf”, and “ST_conf”。_conf存储相应的置信区间，置信水平在95%。可以使用print_to_console=True 打印所有的指数，或者直接取键值。

Si

'S1': array([0.31683154, 0.44376306, 0.01220312]),
 'S1_conf': array([0.06314249, 0.05230396, 0.05764901]),
 'ST': array([0.55586009, 0.44189807, 0.24467539]),
 'ST_conf': array([0.08582851, 0.04184123, 0.02424759]),
 'S2': array([[        nan,  0.00925429,  0.23817211],
        [        nan,         nan, -0.0048877 ],
        [        nan,         nan,         nan]]),
 'S2_conf': array([[       nan, 0.08325501, 0.10813299],
        [       nan,        nan, 0.06117807],
        [       nan,        nan,        nan]])

print(Si['S1'])

[0.31683154 0.44376306 0.01220312]

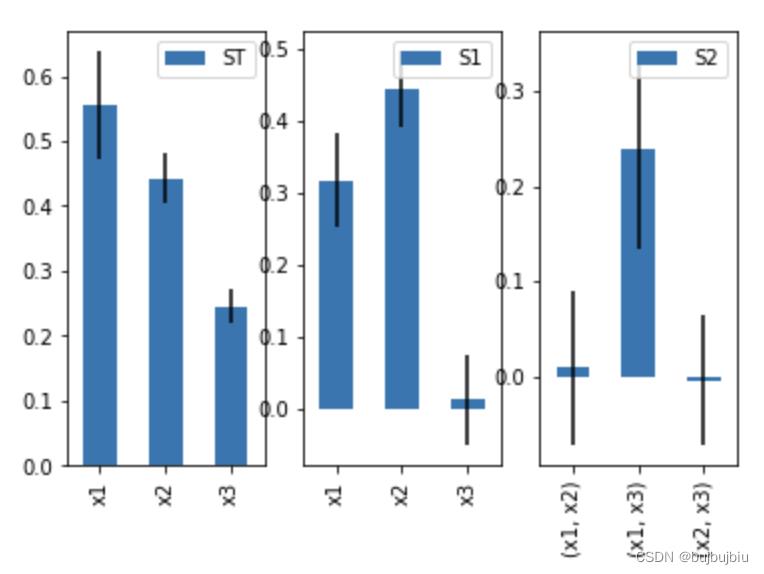
可以看出x1和x2表现出了一阶灵敏性，但是x3没有一阶效应

如果总阶指数基本上比一阶指数大，则可能发生了高阶交互作用，可以查看二阶指数

print('x1-x2:',Si['S2'][0,1])
print('x1-x3:',Si['S2'][0,2])
print('x2-x3:',Si['S2'][1,2])

x1-x2: 0.00925429303490799
x1-x3: 0.2381721095685646
x2-x3: -0.004887704633467273

x1和x3之间有较强的交互，有时也会出现计算误差，如x2-x3指数为负，随着样本的增加，这些误差会缩小。
输出也可以变成Pandas DataFrame从而进行其它分析

total_si,first_si,second_si = Si.to_df()
second_si

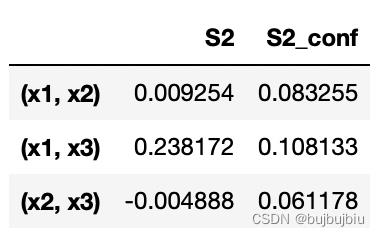
6.绘图

为了方便起见，SALib提供了基本的绘图功能

Si.plot()

案例2

当你想要分析的模型依赖于不是敏感性分析的参数（如位置和时间），则可以单独对每个时间/位置进行分析。以抛物线函数为例

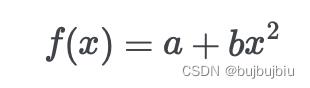
参数a，b将接受敏感性分析，但是x不会
首先导入需要的库

import numpy as np
import matplotlib.pyplot as plt

from SALib.sample import saltelli
from SALib.analyze import sobol

定义抛物线函数

def parabola(x,a,b):
    return a + b*x**2

字典描述只包含a，b的问题

problem = 
    'num_vars':2,
    'names':['a','b'],
    'bounds':[[0,1]]*2

采样，评估，分析。此例中选举100个x的取值，针对需要进行敏感性分析的a,b的每个样本（共384个）计算y值，因此y的大小为(384, 100)

param_values = saltelli.sample(problem,2**6)
print(param_values.shape)

(384, 2)

x = np.linspace(-1,1,100)
y = np.array([parabola(x,*params) for params in param_values])

print(x.shape)
print(y.shape)

(100,)
(384, 100)

print(y)

[[0.421875   0.40593913 0.39032847 ... 0.39032847 0.40593913 0.421875  ]
 [1.21875    1.20281413 1.18720347 ... 1.18720347 1.20281413 1.21875   ]
 [0.859375   0.82594091 0.79318915 ... 0.79318915 0.82594091 0.859375  ]
 ...
 [0.640625   0.61531508 0.59052169 ... 0.59052169 0.61531508 0.640625  ]
 [1.21875    1.19219021 1.16617246 ... 1.16617246 1.19219021 1.21875   ]
 [1.1875     1.16219008 1.13739669 ... 1.13739669 1.16219008 1.1875    ]]

此例中的敏感性指数是一个长度为100的列表，每个元素是一个如上例中的字典

sobol_indices = [sobol.analyze(problem,Y) for Y in y.T]
sobol_indices[0]

'S1': array([0.49526584, 0.49526584]),
 'S1_conf': array([0.17061222, 0.21853518]),
 'ST': array([0.49745084, 0.49672251]),
 'ST_conf': array([0.15376801, 0.16325137]),
 'S2': array([[       nan, 0.00436999],
        [       nan,        nan]]),
 'S2_conf': array([[       nan, 0.39998034],
        [       nan,        nan]])

len(sobol_indices)

100

接下来单独分析每个x对应的指数，提取一阶指数绘图

# 提取100个a,b一阶指数
S1s = np.array([s['S1'] for s in sobol_indices])

fig = plt.figure(figsize=(10,6),constrained_layout = True)
gs = fig.add_gridspec(2,2)

ax0 = fig.add_subplot(gs[:,0])
ax1 = fig.add_subplot(gs[0,1])
ax2 = fig.add_subplot(gs[1,1])

for i,ax in enumerate([ax1,ax2]):
    ax.plot(x,S1s[:,i],
           label=r'S1$_\\mathregular$'.format(problem["names"][i]),
           color = 'black')
    ax.set_xlabel('x')
    ax.set_ylabel('First-order Sobol index')
    ax.set_ylim(0,1.04)
    ax.yaxis.set_label_position("right")
    ax.yaxis.tick_right()
    ax.legend(loc='upper right')
    
ax0.plot(x,np.mean(y,axis=0),label="Mean", color='black')
prediction_interval = 95
ax0.fill_between(x,
                 np.percentile(y, 50 - prediction_interval/2., axis=0),
                 np.percentile(y, 50 + prediction_interval/2., axis=0),
                 alpha=0.5, color='black',
                 label=f"prediction_interval % prediction interval")
ax0.set_xlabel("x")
ax0.set_ylabel("y")
ax0.legend(title=r"$y=a+b\\cdot x^2$",
           loc='upper center')._legend_box.align = "left"

plt.show()

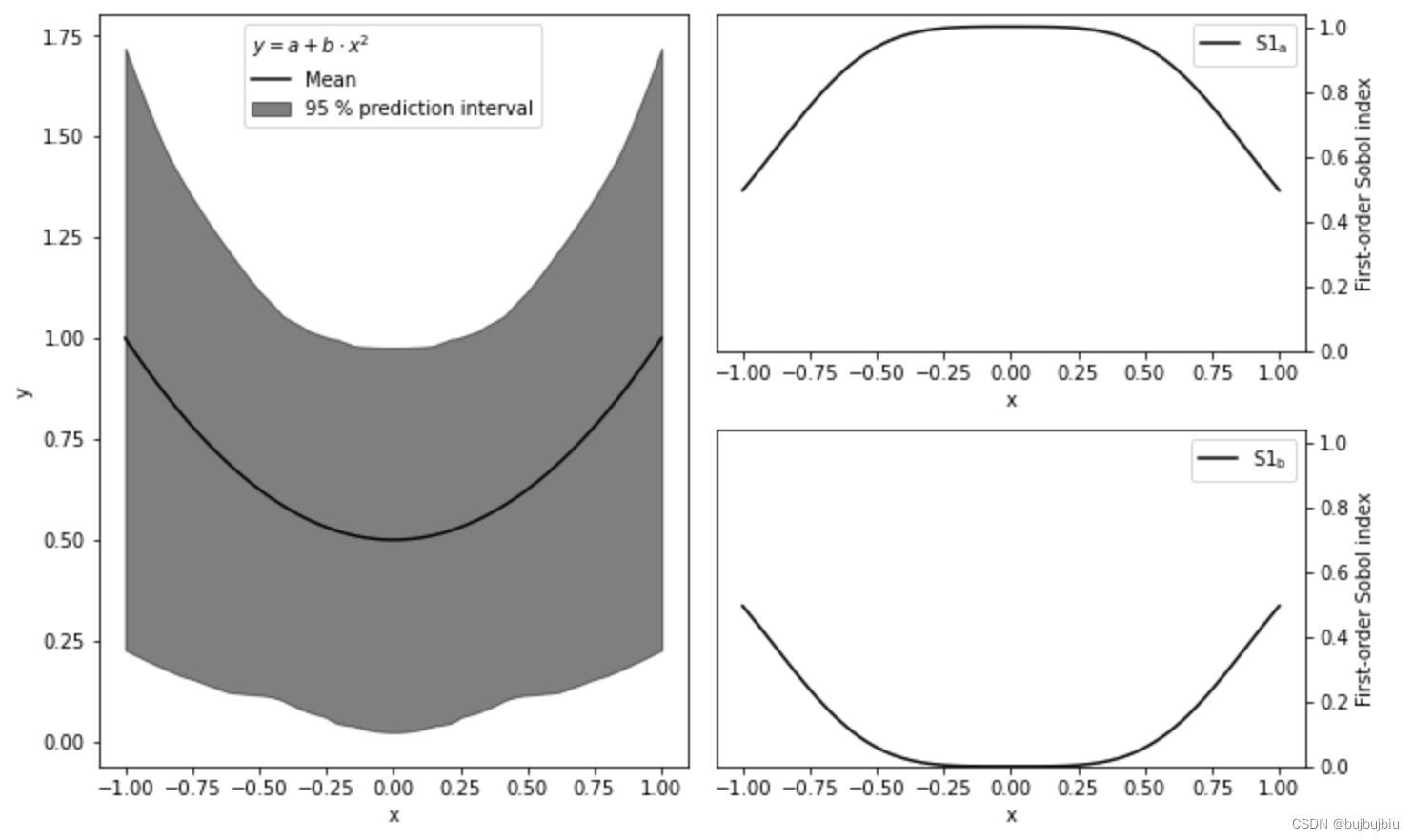
左图为每个x对应不同a,b取值下y的均值以及95%置信区间，右图为参数a,b的一阶指数。由图可知，在x=0时，y完全由参数a决定，参数b由于x而消失，x的绝对值越大，参数b对变化贡献越大，参数a相应越小

SAlib（灵敏度分析）包是否仅支持一个列（向量）输入？

我想用作SAlib分析（SOBOL）参数的模型输出数组的形状不符合sobol需要的数组形状。

1. 我有一个参数数组，其形状为（28,13），由SAlib包的saltelli函数生成。
2. 另一方面，我的模型在许多时间点计算解决方案，比如200.所以最后我有一个输出数组（28,200）
3. 我必须使用此输出数组作为SAlib的Sobol函数的参数。
4. 但据我所知，从SAlib的doc中的例子来看，Sobol的输入参数必须有一个列数组，如（28，）

我想学习的是，我是否从SAlib的文档中推断出正确的结论，因为SAlib的Sobol函数只需要一个列数组？或者我可以用（28,200）数组喂它吗？

PS：实际上我试过（28,200）并且遇到了一些错误。但我不确定SAlib是否支持（28,200）的数组形状或者我的代码是否有错误。

from SALib.sample import saltelli
from SALib.analyze import sobol,morris
from SALib.test_functions import Ishigami  

input_dict = {}
problem = {'num_vars':13,'names': 
['Rp1','Ra','Rv','Rp2','Cla','Csa','Clv','Csv','Emin','Emax','R1','R2','C1'],\
       'bounds':[[1.0,2.0],[0.1,0.5],[0.01,0.1],[11.0,15.0],[0.1,1.5],[0.05,0.55],[30.0,50.0],[2.0,6.0],\
                 [0.001,0.45],[0.2,3.2],[25.0,42.0],[2.0,8.0],[15.0,19.0]]}

param_values = saltelli.sample(problem,1)
for count, param in enumerate(param_values):
    input_dict[count] = param

kwargs = {}
kwargs['newly_defined_parameters']= input_dict

sol_dict = main(**kwargs) # main function solves the model and returns a solution dictionary

我的模型产生8个输出。但我想只对1个输出进行灵敏度分析。所以我把输出数据加载到my_sol数组中。

my_sol = np.zeros((28,200))
for ps in range(28):         #ps ---> parameter set
    for tp in range(200):    #tp ---> time point
        my_sol[ps][tp]=sol_dict[ps][1][tp] 

my_sol.shape
(28, 200)

现在分析部分：

Si = sobol.analyze(problem,my_sol)

现在错误部分：

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-39-ab30c1d4df01> in <module>
----> 1 Si = sobol.analyze(problem,my_sol)

C:\ProgramData\Anaconda3\lib\site-packages\SALib\analyze\sobol.py in analyze(problem, Y, calc_second_order, num_resamples, conf_level, print_to_console, parallel, n_processors, seed)
    101 
    102         for j in range(D):
--> 103             S['S1'][j] = first_order(A, AB[:, j], B)
    104             S['S1_conf'][j] = Z * first_order(A[r], AB[r, j], B[r]).std(ddof=1)
105             S['ST'][j] = total_order(A, AB[:, j], B)

ValueError: setting an array element with a sequence.

答案

使用SAlib，我无法对我的模型的时间序列输出进行灵敏度分析，该模型是（28,200）的数组。相反，我试过两种不同的方式。

1st：我为evey时间点制作了SA，因此我能够在模型运行时绘制参数的灵敏度变化。而且我通过这种方式计算了灵敏度指数的平均值，我得到了最终的SA指数。

第二：我计算了每个时间序列的平均值，并为这些最终平均值做了SA。

（第一个选项以更合理的解决方案结束）

https://github.com/SALib/SALib/issues/233