Pytorch深度学习实战3-5：详解计算图与自动微分机(附实例)

Posted 2023-04-02 Mr.Winter`

目录

• 1 计算图原理
• 2 基于计算图的传播
• 3 神经网络计算图
• 4 自动微分机
• 5 Pytorch中的自动微分
• • 5.1 梯度缓存
  • 5.2 参数冻结

1 计算图原理

计算图(Computational Graph)是机器学习领域中推导神经网络和其他模型算法，以及软件编程实现的有效工具。

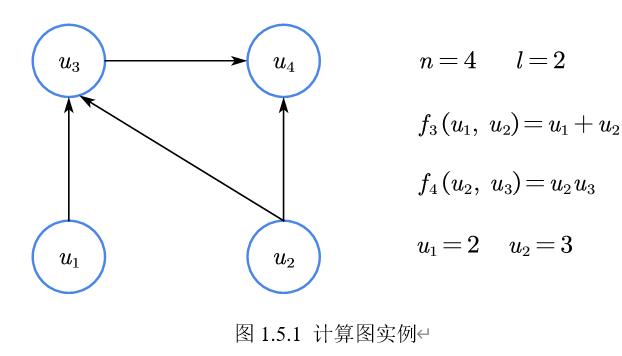
计算图的核心是将模型表示成一张拓扑有序(Topologically Ordered)的有向无环图(Directed Acyclic Graph)，其中每个节点$u_i$包含数值信息(可以是标量、向量、矩阵或张量)和算子信息$f_i$。拓扑有序指当前节点仅在全体指向它的节点被计算后才进行计算。

计算图的优点在于：

• 可以通过基本初等映射 的拓扑联结，形成复合的复杂模型，大多数神经网络模型都可以被计算图表示；
• 便于实现自动微分机(Automatic Differentiation Machine)，对给定计算图可基于链式法则由节点局部梯度进行反向传播。

计算图的基本概念如表所示，基于计算图的基本前向传播和反向传播算法如表

符号	含义
$n$	计算图的节点数
$l$	计算图的叶节点数
$L$	计算图的叶节点索引集
$C$	计算图的非叶节点索引集
$E$	计算图的有向边集合
$u_i$	计算图中的第$i$节点或其值
$d_i$	$u_i$ 的维度
$f_i$	$u_i$的算子
${\alpha }_i$	$u_i$的全体关联输入
${\mathbf{J}}_{j\to i}$	节点$u_i$关于节点$u_j$的雅克比矩阵
${\mathbf{P}}_i$	输出节点关于输入节点的雅克比矩阵

2 基于计算图的传播

基于计算图的前向传播算法如下

基于计算图的反向传播算法如下

以第一节的图为例，可知$E=\left(1,3\right),\left(2,3\right),\left(2,4\right),\left(3,4\right)$。首先进行前向传播：

$$\begin{array}{l}{u}_3=u_1+u_2=5\\ u_4=u_2{u}_3=15\end{array}$$

$$\{\begin{array}{l}{\mathbf{J}}_{1\to 3}=\partial u_3/\partial u_1=1\\ {\mathbf{J}}_{2\to 3}=\partial u_3/\partial u_2=1\\ {\mathbf{J}}_{2\to 4}=\partial u_4/\partial u_2=u_3=5\\ {\mathbf{J}}_{3\to 4}=\partial u_4/\partial u_3=u_2=3\end{array}$$

接着进行反向传播：

$$\{\begin{array}{l}{\mathbf{P}}_4=1\\ {\mathbf{P}}_3={\mathbf{P}}_4{\mathbf{J}}_{3\to 4}=3\\ {\mathbf{P}}_2={\mathbf{P}}_4{\mathbf{J}}_{2\to 4}+{\mathbf{P}}_3{\mathbf{J}}_{2\to 3}=8\\ {\mathbf{P}}_1={\mathbf{P}}_3{\mathbf{J}}_{1\to 3}=3\end{array}$$

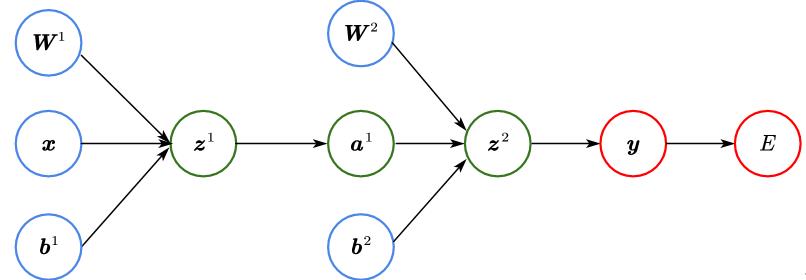
3 神经网络计算图

一个神经网络的计算图实例如下，所有参数都可以用之前的模型表示

L u 1 = W 1 ∈ R n 1 × n 0 u 2 = b 1 ∈ R n 1

参考《深度学习之PyTorch实战计算机视觉》PDF

计算机视觉、自然语言处理和语音识别是目前深度学习领域很热门的三大应用方向。

计算机视觉学习，推荐阅读《深度学习之PyTorch实战计算机视觉》。学到人工智能的基础概念及Python 编程技能，掌握PyTorch 的使用方法，学到深度学习相关的理论知识，比如卷积神经网络、循环神经网络、自动编码器，等等。在掌握深度学习理论和编程技能之后，还会学到如何基于PyTorch 深度学习框架实战计算机视觉。《深度学习之PyTorch实战计算机视觉》中的大量实例在循序渐进地学习的同时，不断地获得成就感。

学习参考：

《深度学习之PyTorch实战计算机视觉》

两个版本的高清PDF，287页，带书签目录，文字可以复制。

网盘下载：http://106.13.73.98

以上是关于Pytorch深度学习实战3-5：详解计算图与自动微分机(附实例)的主要内容，如果未能解决你的问题，请参考以下文章

深度学习-PyTorch框架实战系列

《深度学习与计算机视觉算法原理框架应用》PDF+《深度学习之PyTorch实战计算机视觉》PDF

深度学习-Pytorch张量tensor详解（线性回归实战）

深度之眼PyTorch训练营第二期 ---3计算图与动态图机制

Pytorch深度学习实战3-7：详解数据加载DataLoader与模型处理

[十九]深度学习Pytorch-可视化工具TensorBoard