Python数学建模—线性规划
Posted 猿童学
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python数学建模—线性规划相关的知识，希望对你有一定的参考价值。
我是猿童学，本文是根据司守奎老师《数学建模算法与程序》的书本内容编写，使用其书中案例，书中的编程语言是MATLAB、Lingo，我将使用Python来解决问题。接下来的一个月我将学习使用Python来解决数学建模问题。将记录下学习中的笔记和部分案例。
1、线性规划
1.1 线性规划的实例与定义
例 1 某机床厂生产甲、乙两种机床每台销售后的利润分别为 4000 元与3000元。 生产甲机床需用 A、B 机器加工，加工时间分别为每台 2 小时和1小时生产乙机床需用 A、B、C 三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为 A 机器 10 小时、B 机器 8 小时和C 机器 7 小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？
上述问题的数学模型：设该厂生产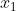 
台甲机床和
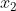乙机床时总利润最大，则
应满足：
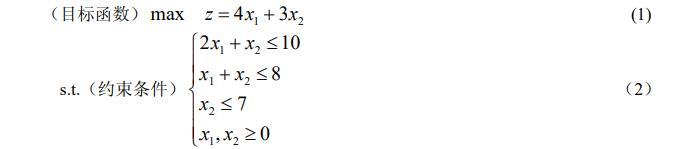
这里变量 称之为决策变量，（1）式被称为问题的目标函数，（2）中的几个不等式 是问题的约束条件，记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性 函数，故被称为线性规划问题。总之，线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最 小的问题。
1.2 使用Python中的scipy库求解列 1 线性规划问题：
线性规划的标准型为
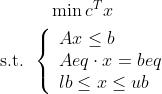（3）
其中，c是价值向量；A和b对应线性不等式约束；Aeq和beq对应线性等式约束；bounds对应公式中的lb和ub，决策向量的下界和上界。
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simplex', callback=None, options=None)
输入参数解析：
- c：线性目标函数的系数
- A_ub（可选参数）：不等式约束矩阵，
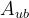的每一行指定x上的线性不等式约束的系数 - b_ub（可选参数）：不等式约束向量，每个元素代表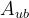x的上限
- A_eq（可选参数）：等式约束矩阵，
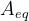的每一行指定x xx上的线性等式约束的系数 - b_eq（可选参数）：等式约束向量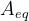，的每个元素必须等于
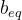的对应元素 - bounds（可选参数）：定义决策变量x的最小值和最大值
- 数据类型： (min, max)序列对
- None：使用None表示没有界限，默认情况下，界限为（0，None）（所有决策变量均为非负数）
- 如果提供一个元组(min, max)，则最小值和最大值将用作所有决策变量的界限。
输出参数解析：
- x：在满足约束的情况下将目标函数最小化的决策变量的值
- fun：目标函数的最优值（
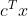） - slack：不等式约束的松弛值（名义上为正值）
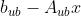
- con：等式约束的残差（名义上为零）
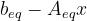
- success：当算法成功找到最佳解决方案时为 True
- status：表示算法退出状态的整数
- 0 : 优化成功终止
- 1 : 达到了迭代限制
- 2 : 问题似乎不可行
- 3 : 问题似乎是不收敛
- 4 : 遇到数值困难
- nit：在所有阶段中执行的迭代总数
- message：算法退出状态的字符串描述符
使用scipy库来解决例1：
from scipy.optimize import linprog
c = [-4, -3] #目标函数的系数
A= [[2, 1], [1, 1],[0,1]] #<=不等式左侧未知数系数矩阵
b = [10,8,7] # <=不等式右侧常数矩阵
#A_eq = [[]] #等式左侧未知数系数矩阵
#B_eq = [] #等式右侧常数矩阵
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
res =linprog(c, A, b, bounds=(x1, x2))#默认求解最小值，求解最大值使用-c并取结果相反数
print(res)
输出结果：
con: array([], dtype=float64)
fun: -25.999999999841208
message: 'Optimization terminated successfully.'
nit: 5
slack: array([8.02629074e-11, 3.92663679e-11, 1.00000000e+00])
status: 0
success: True
x: array([2., 6.])fun为目标函数的最优值，slack为松弛变量，status表示优化结果状态，x为最优解。
此模型的求解结果为：当x1=2，x2=6时，函数取得最优值25.999999999841208。
例 2 求解下列线性规划问题：
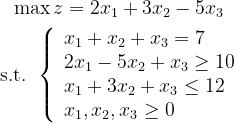
注意要先标准化！
这里使用另一种比较规范的写法：
from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
x3 = [0, None] #未知数取值范围
res = optimize.linprog(-c,A,B,Aeq,Beq,bounds=(x1, x2, x3))
print(res)输出结果：
con: array([1.80713489e-09])
fun: -14.571428565645054
message: 'Optimization terminated successfully.'
nit: 5
slack: array([-2.24579466e-10, 3.85714286e+00])
status: 0
success: True
x: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])此模型的求解结果为：当x1=6.4，x2=5.7，x3=2.3时，函数取得最优值14.571428565645054
例3 求解线性规划问题：
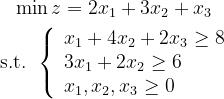
使用Python编写：
from scipy import optimize
import numpy as np
c = np.array([2,3,1])
A = np.array([[1,4,2],[3,2,0]])
B = np.array([8,6])
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
x3 = [0, None] #未知数取值范围
res = optimize.linprog(c,-A,-B,bounds=(x1, x2, x3))
print(res)
输出结果：
con: array([], dtype=float64)
fun: 6.999999994872993
message: 'Optimization terminated successfully.'
nit: 3
slack: array([ 3.85261245e-09, -1.41066261e-08])
status: 0
success: True
x: array([1.17949641, 1.23075538, 0.94874104])此模型的求解结果为：当x1=1.1，x2=1.2，x3=0.9时，函数取得最优值6.999999994872993
2、运输问题
2.1产销平衡的数学建模过程：
例 6 某商品有
个产地、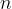
个销地，各产地的产量分别为
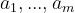，各销地的需求量分别为
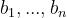。若该商品由 
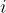产地运到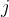 
销地的单位运价为
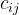，问应该如何调运才能使总运费最省？
解：引入变量 
，其取值为由 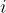产地运往 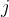销地的该商品数量，数学模型为
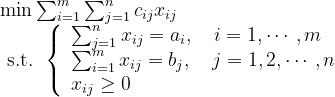
显然是一个线性规划问题，当然可以用单纯形法求解。
对产销平衡的运输问题，由于有以下关系式存在：
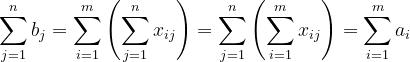
其约束条件的系数矩阵相当特殊，可用比较简单的计算方法，习惯上称为表上作业法（由 康托洛维奇和希奇柯克两人独立地提出，简称康—希表上作业法），下面使用例子来讲解。
2.2 产销平衡的运输问题
1.问题描述
某公司下属有甲、乙、丙三个工厂，分别向A、B、C、D四个销地提供产品，产量、需求量及工厂到销售地的运价（单位：元/吨）如下表所示，求使费用最少的最佳运输方案。
| 工厂 \\ 销地 | A | B | C | D | 产量（吨） |
| 甲 | 8 | 6 | 10 | 9 | 18 |
| 乙 | 9 | 12 | 13 | 1 | 18 |
| 丙 | 14 | 12 | 16 | 5 | 19 |
| 销量（吨） | 16 | 15 | 7 | 17 | 55 |
2.问题解析
总产量=18+18+19=55
总销量=16+15+7+17=55
产量等于销量，即这是产销平衡的运输问题。直接采用表上作业法进行求解。
3.使用python求解：
# 运输问题求解：使用Vogel逼近法寻找初始基本可行解
import numpy as np
import copy
import pandas as pd
def main():
# mat = pd.read_csv('表上作业法求解运输问题.csv', header=None).values
# mat = pd.read_excel('表上作业法求解运输问题.xlsx', header=None).values
a = np.array([18, 18, 19]) # 产量
b = np.array([16, 15, 7, 17]) # 销量
c = np.array([[8, 6, 10, 9], [9, 12, 13, 7], [14, 12, 16, 5]])
# [c, x] = TP_vogel(mat)
[c,x]=TP_vogel([c,a,b])
def TP_split_matrix(mat): # 运输分割矩阵
c = mat[:-1, :-1]
a = mat[:-1, -1]
b = mat[-1, :-1]
return (c, a, b)
def TP_vogel(var): # Vogel法代码，变量var可以是以numpy.ndarray保存的运输表，或以tuple或list保存的(成本矩阵,供给向量,需求向量)
import numpy
typevar1 = type(var) == numpy.ndarray
typevar2 = type(var) == tuple
typevar3 = type(var) == list
if typevar1 == False and typevar2 == False and typevar3 == False:
print('>>>非法变量<<<')
(cost, x) = (None, None)
else:
if typevar1 == True:
[c, a, b] = TP_split_matrix(var)
elif typevar2 == True or typevar3 == True:
[c, a, b] = var
cost = copy.deepcopy(c)
x = np.zeros(c.shape)
M = pow(10, 9)
for factor in c.reshape(1, -1)[0]:
p = 1
while int(factor) != M:
if np.all(c == M):
break
else:
print('第1次迭代！')
print('c:\\n', c)
# 获取行/列最小值数组
row_mini1 = []
row_mini2 = []
for row in range(c.shape[0]):
Row = list(c[row, :])
row_min = min(Row)
row_mini1.append(row_min)
Row.remove(row_min)
row_2nd_min = min(Row)
row_mini2.append(row_2nd_min)
# print(row_mini1,'\\n',row_mini2)
r_pun = [row_mini2[i] - row_mini1[i] for i in range(len(row_mini1))]
print('行罚数：', r_pun)
# 计算列罚数
col_mini1 = []
col_mini2 = []
for col in range(c.shape[1]):
Col = list(c[:, col])
col_min = min(Col)
col_mini1.append(col_min)
Col.remove(col_min)
col_2nd_min = min(Col)
col_mini2.append(col_2nd_min)
c_pun = [col_mini2[i] - col_mini1[i] for i in range(len(col_mini1))]
print('列罚数：', c_pun)
pun = copy.deepcopy(r_pun)
pun.extend(c_pun)
print('罚数向量：', pun)
max_pun = max(pun)
max_pun_index = pun.index(max(pun))
max_pun_num = max_pun_index + 1
print('最大罚数：', max_pun, '元素序号：', max_pun_num)
if max_pun_num <= len(r_pun):
row_num = max_pun_num
print('对第', row_num, '行进行操作：')
row_index = row_num - 1
catch_row = c[row_index, :]
print(catch_row)
min_cost_colindex = int(np.argwhere(catch_row == min(catch_row)))
print('最小成本所在列索引：', min_cost_colindex)
if a[row_index] <= b[min_cost_colindex]:
x[row_index, min_cost_colindex] = a[row_index]
c1 = copy.deepcopy(c)
c1[row_index, :] = [M] * c1.shape[1]
b[min_cost_colindex] -= a[row_index]
a[row_index] -= a[row_index]
else:
x[row_index, min_cost_colindex] = b[min_cost_colindex]
c1 = copy.deepcopy(c)
c1[:, min_cost_colindex] = [M] * c1.shape[0]
a[row_index] -= b[min_cost_colindex]
b[min_cost_colindex] -= b[min_cost_colindex]
else:
col_num = max_pun_num - len(r_pun)
col_index = col_num - 1
print('对第', col_num, '列进行操作：')
catch_col = c[:, col_index]
print(catch_col)
# 寻找最大罚数所在行/列的最小成本系数
min_cost_rowindex = int(np.argwhere(catch_col == min(catch_col)))
print('最小成本所在行索引：', min_cost_rowindex)
# 计算将该位置应填入x矩阵的数值（a,b中较小值）
if a[min_cost_rowindex] <= b[col_index]:
x[min_cost_rowindex, col_index] = a[min_cost_rowindex]
c1 = copy.deepcopy(c)
c1[min_cost_rowindex, :] = [M] * c1.shape[1]
b[col_index] -= a[min_cost_rowindex]
a[min_cost_rowindex] -= a[min_cost_rowindex]
else:
x[min_cost_rowindex, col_index] = b[col_index]
# 填入后删除已满足/耗尽资源系数的行/列，得到剩余的成本矩阵，并改写资源系数
c1 = copy.deepcopy(c)
c1[:, col_index] = [M] * c1.shape[0]
a[min_cost_rowindex] -= b[col_index]
b[col_index] -= b[col_index]
c = c1
print('本次迭代后的x矩阵：\\n', x)
print('a:', a)
print('b:', b)
print('c:\\n', c)
if np.all(c == M):
print('【迭代完成】')
print('-' * 60)
else:
print('【迭代未完成】')
print('-' * 60)
p += 1
print(f"第p次迭代！")
total_cost = np.sum(np.multiply(x, cost))
if np.all(a == 0):
if np.all(b == 0):
print('>>>供求平衡<<<')
else:
print('>>>供不应求，需求方有余量<<<')
elif np.all(b == 0):
print('>>>供大于求，供给方有余量<<<')
else:
print('>>>无法找到初始基可行解<<<')
print('>>>初始基本可行解x*：\\n', x)
print('>>>当前总成本：', total_cost)
[m, n] = x.shape
varnum = np.array(np.nonzero(x)).shape[1]
if varnum != m + n - 1:
print('【注意：问题含有退化解】')
return (cost, x)
if __name__ == '__main__':
main()输出结果：
D:\\Anaconda\\python.exe D:/PyCharm/数学建模/线性规划/www.py
第1次迭代！
c:
[[ 8 6 10 9]
[ 9 12 13 7]
[14 12 16 5]]
行罚数： [2, 2, 7]
列罚数： [1, 6, 3, 2]
罚数向量： [2, 2, 7, 1, 6, 3, 2]
最大罚数： 7 元素序号： 3
对第 3 行进行操作：
[14 12 16 5]
最小成本所在列索引： 3
本次迭代后的x矩阵：
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [18 18 2]
b: [16 15 7 0]
c:
[[ 8 6 10 1000000000]
[ 9 12 13 1000000000]
[ 14 12 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第2次迭代！
第1次迭代！
c:
[[ 8 6 10 1000000000]
[ 9 12 13 1000000000]
[ 14 12 16 1000000000]]
行罚数： [2, 3, 2]
列罚数： [1, 6, 3, 0]
罚数向量： [2, 3, 2, 1, 6, 3, 0]
最大罚数： 6 元素序号： 5
对第 2 列进行操作：
[ 6 12 12]
最小成本所在行索引： 0
本次迭代后的x矩阵：
[[ 0. 15. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [ 3 18 2]
b: [16 0 7 0]
c:
[[ 8 1000000000 10 1000000000]
[ 9 1000000000 13 1000000000]
[ 14 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第3次迭代！
第1次迭代！
c:
[[ 8 1000000000 10 1000000000]
[ 9 1000000000 13 1000000000]
[ 14 1000000000 16 1000000000]]
行罚数： [2, 4, 2]
列罚数： [1, 0, 3, 0]
罚数向量： [2, 4, 2, 1, 0, 3, 0]
最大罚数： 4 元素序号： 2
对第 2 行进行操作：
[ 9 1000000000 13 1000000000]
最小成本所在列索引： 0
本次迭代后的x矩阵：
[[ 0. 15. 0. 0.]
[16. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [3 2 2]
b: [0 0 7 0]
c:
[[1000000000 1000000000 10 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第4次迭代！
第1次迭代！
c:
[[1000000000 1000000000 10 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数： [999999990, 999999987, 999999984]
列罚数： [0, 0, 3, 0]
罚数向量： [999999990, 999999987, 999999984, 0, 0, 3, 0]
最大罚数： 999999990 元素序号： 1
对第 1 行进行操作：
[1000000000 1000000000 10 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
[[ 0. 15. 3. 0.]
[16. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [0 2 2]
b: [0 0 4 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第5次迭代！
第1次迭代！
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数： [0, 999999987, 999999984]
列罚数： [0, 0, 3, 0]
罚数向量： [0, 999999987, 999999984, 0, 0, 3, 0]
最大罚数： 999999987 元素序号： 2
对第 2 行进行操作：
[1000000000 1000000000 13 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 0. 17.]]
a: [0 0 2]
b: [0 0 2 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第6次迭代！
第1次迭代！
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数： [0, 0, 999999984]
列罚数： [0, 0, 999999984, 0]
罚数向量： [0, 0, 999999984, 0, 0, 999999984, 0]
最大罚数： 999999984 元素序号： 3
对第 3 行进行操作：
[1000000000 1000000000 16 1000000000]
最小成本所在列索引： 2
本次迭代后的x矩阵：
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 2. 17.]]
a: [0 0 0]
b: [0 0 0 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]]
【迭代完成】
------------------------------------------------------------
>>>供求平衡<<<
>>>初始基本可行解x*：
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 2. 17.]]
>>>当前总成本： 407.0
进程已结束，退出代码为 0
上面使用的方法是表上作业法，属下所示：
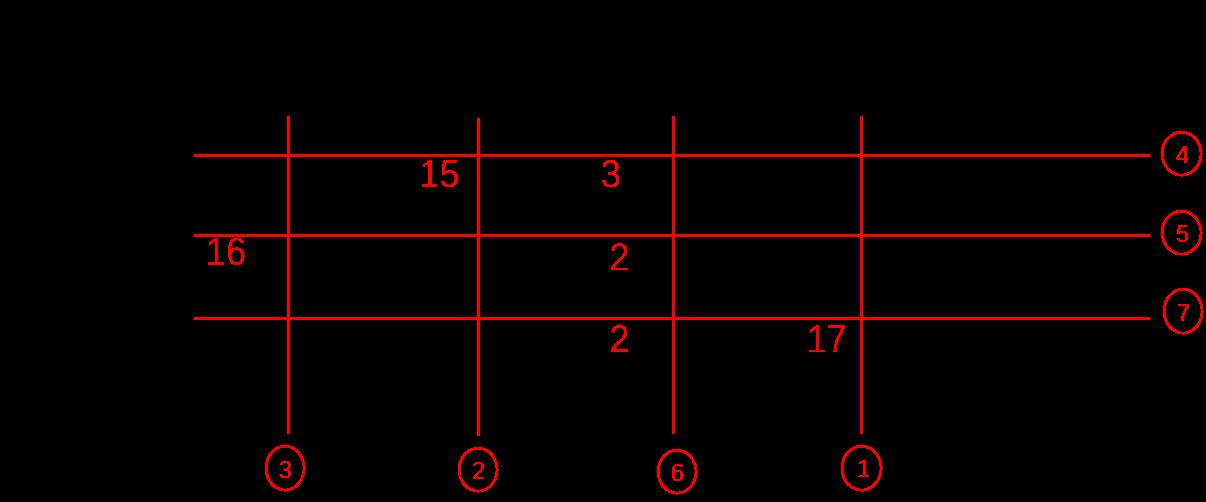
最终最优的总成本： 407.0
2.3 产大于销的运输问题
1.问题描述
有三个牧业基地向4个城市提供鲜奶，4个城市每日的鲜奶需求量、3个基地的每日鲜奶供应量以及运送每千升鲜奶的费用如下表所示，试确定最经济的鲜奶运输方案。
| 城市\\基地 | A | B | c | D | 供应量 |
| 甲 | 3 | 2 | 4 | 5 | 30 |
| 乙 | 2 | 3 | 5 | 3 | 40 |
| 丙 | 1 | 4 | 2 | 4 | 50 |
| 需求量 | 16 | 30 | 24 | 30 |
2.问题解析
总供应量=30+40+50=120
总需求量=16+30+24+30=100
供过于求，即产量大于销量，这是一个产大于销的运输问题。要将问题转化为产销平衡的运输问题，需进行以下几个方面的调整。
（1）增加一个虚拟销地E，使其总需求量为120-100=20。
（2）由于销地是虚拟的，实际上是产量过剩的物资在产地就地储存，所以不会产生实际的运输，即不会产生运费。
因此新的供需量及单位运价表如下所示。
| 城市\\基地 | A | B | c | D | E | 供应量 |
| 甲 | 3 | 2 | 4 | 5 | 0 | 30 |
| 乙 | 2 | 3 | 5 | 3 | 0 | 40 |
| 丙 | 1 | 4 | 2 | 4 | 0 | 50 |
| 需求量 | 16 | 30 | 24 | 30 | 20 | 120 |
3.问题求解
使用python来实现：
这里也可以使用（最小元素法）来解决:
'----------------------------------------最小元素法------------------------------------' \\
'最小元素法是指有限满足单位运价最小的供销服务'
import numpy as np
import copy
supplyNum = 3 # 供应商数量
demandNum = 5 # 需求商数量
A = np.array([30,40,50]) # 产量
B = np.array([16,30,24,30,20]) # 销量
C = np.array([[3,2,4,5,0], [2,3,5,3,0], [1,4,2,4,0]]) # 成本
X = np.zeros((supplyNum, demandNum)) # 初始解
c = copy.deepcopy(C)
maxNumber = 10000 # 极大数
def pivot(A, B, c, X):
index = np.where(c == np.min(c)) # 寻找最小值的索引
minIndex = (index[0][0], index[1][0]) # 确定最小值的索引
# 确定应该优先分配的量，并且改变价格
if A[index[0][0]] > B[index[1][0]]:
X[minIndex] = B[index[1][0]]
c[:, index[1][0]] = maxNumber # 改变价格
A[index[0][0]] = A[index[0][0]] - B[index[1][0]]
B[index[1][0]] = 0 # 改变销量
else:
X[minIndex] = A[index[0][0]]
c[index[0][0], :] = maxNumber
B[index[1][0]] = B[index[1][0]] - A[index[0][0]]
A[index[0][0]] = 0
return A, B, c, X
# 最小元素法
def minimumElementMethod(A, B, c, X):
while (c < maxNumber).any():
A, B, c, X = pivot(A, B, c, X)
return X
solutionMin = minimumElementMethod(A, B, c, X)
print('最小元素法得到的初始解为：')
print(solutionMin)
print('最小元素法得到的总运费为:', ((solutionMin * C).sum()))
输出结果：
最小元素法得到的初始解为：
[[ 0. 10. 0. 0. 20.]
[ 0. 20. 0. 20. 0.]
[16. 0. 24. 10. 0.]]
最小元素法得到的总运费为: 244.02.4 产小于销的运输问题
1.问题描述
某三个煤炭厂供应4个地区，假定等量的煤炭在这些地区使用效果相同，已知各煤炭厂年产量，各地区的需要量及从各煤炭厂到各地区的单位运价表如下所示，试决定最优的调运方案。
| 销地\\产地 | B1 | B2 | B3 | B4 | 产量 |
| A1 | 5 | 3 | 10 | 4 | 90 |
| A2 | 2 | 6 | 9 | 6 | 40 |
| A3 | 14 | 10 | 5 | 7 | 70 |
| 销量 | 30 | 50 | 100 | 40 |
2.问题解析
总供应量=30+40+50=120
总需求量=16+30+24+30=100
供过于求，即产量大于销量，这是一个产大于销的运输问题。要将问题转化为产销平衡的运输问题，需进行以下几个方面的调整。
（1）增加一个虚拟销地E，使其总需求量为120-100=20。
（2）由于销地是虚拟的，实际上是产量过剩的物资在产地就地储存，所以不会产生实际的运输，即不会产生运费。
因此新的供需量及单位运价表如下所示。
| 销地\\产地 | B | B | B3 | B4 | 产量 |
| A, | 5 | 3 | 10 | 4 | 90 |
| A2 | 2 | 6 | 9 | 6 | 40 |
| A3 | 14 | 10 | 5 | 7 | 70 |
| A4 | 0 | 0 | 0 | 0 | 20 |
| 销量 | 30 | 50 | 100 | 40 | 220 |
3.问题求解
使用python求解：
这里可以使用（Vogel逼近法）寻找初始基本可行解
'-----------------------------------Vogel法---------------------------------'
supplyNum = 4 # 供应商数量
demandNum = 4 # 需求商数量
A = np.array([90,40,70,20]) # 产量
B = np.array([30,50,100,40]) # 销量
C = np.array([[5,3,10,4], [2,6,9,6], [14,10,5,7],[0,0,0,0]]) # 成本
X = np.zeros((supplyNum, demandNum)) # 初始解
c = copy.deepcopy(C)
numPunish = [0] * (supplyNum + demandNum) # 整体罚数
def pivot(X, A, B, C):
# 求解罚数，其中列罚数排在行罚数后面
for i in range(supplyNum):
sortList = np.sort(C[i, :])
numPunish[i] = sortList[1] - sortList[0]
for i in range(demandNum):
sortList = np.sort(C[:, i])
numPunish[i + supplyNum] = sortList[1] - sortList[0]
maxIndex = np.argmax(numPunish) # 寻找最大罚数的索引
# 若最大的罚数属于行罚数
if maxIndex < supplyNum:
minIndex = np.argmin(C[maxIndex, :])
index = (maxIndex, minIndex) # 得到最大罚数的一行中最小的运价
# 若产量大于销量
if A[maxIndex] > B[minIndex]:
X[index] = B[minIndex] # 更新解
C[:, minIndex] = maxNumber # 将已经满足的一列中的运价增大替代删除操作
A[maxIndex] -= B[minIndex] # 更新剩余产量
B[minIndex] = 0 # 更新已经满足的销量
# 若销量大于产量
else:
X[index] = A[maxIndex]
C[maxIndex, :] = maxNumber
B[minIndex] -= A[maxIndex] # 更新销量
A[maxIndex] = 0
# 若最大的罚数为列罚数
else:
minIndex = np.argmin(C[:, maxIndex - supplyNum]) # 这时maxIndex-supplyNum是罚数最大的列
index = (minIndex, maxIndex - supplyNum)
if A[minIndex] > B[maxIndex - supplyNum]: # 这里是产量大于销量，因此有限满足销量
X[index] = B[maxIndex - supplyNum]
C[:, maxIndex - supplyNum] = maxNumber
A[minIndex] -= B[maxIndex - supplyNum]
B[maxIndex - supplyNum] = 0
else:
X[index] = A[minIndex]
C[minIndex, :] = maxNumber
B[maxIndex - supplyNum] -= A[minIndex]
A[minIndex] = 0
return X, A, B, C
# 沃格尔法得到初始解
def Vogel(A, B, C):
X = np.zeros((supplyNum, demandNum)) # 初始解
numPunish = [0] * (supplyNum + demandNum) # 整体罚数
# 迭代，直到所有的产量和销量全部满足
while (A != 0).any() and (B != 0).any():
X, A, B, C = pivot(X, A, B, C)
return X
# 上面对于条件的判断，还需要对销量和需求量进行改变
solutionVogel = Vogel(A, B, c)
print('Vogel法得到的初始解为：')
print(solutionVogel)
print('Vogel法得到的总运费为:', (C * solutionVogel).sum())输出结果：
Vogel法得到的初始解为：
[[ 0. 50. 0. 40.]
[30. 0. 10. 0.]
[ 0. 0. 70. 0.]
[ 0. 0. 20. 0.]]
Vogel法得到的总运费为: 810.0上面三种产销问题是常见的情况，除了产销问题还有弹性需求的运输问题、中间转运的运输问题。
这里就不罗嗦了，自己查资料噢！
3、指派问题
3.1 指派问题的数学模型
例 7 拟分配 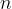人去干 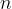项工作，每人干且仅干一项工作，若分配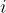第 人去干第 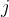项工作，需花费 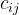单位时间，问应如何分配工作才能使工人花费的总时间最少？
容易看出，要给出一个指派问题的实例，只需给出矩阵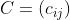
， 
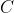被称为指派 问题的系数矩阵。 引入变量 
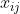，若分配 
干 
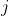工作，则取 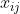= 1，否则取 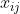= 0 。上述指派问题的数学模型为：
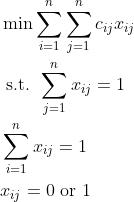
述指派问题的可行解可以用一个矩阵表示，其每行每列均有且只有一个元素为 1，其余元素均为 0；可以用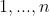
中的一个置换表示。
问题中的变量只能取 0 或 1，从而是一个 0-1 规划问题。一般的 0-1 规划问题求解 极为困难。但指派问题并不难解，其约束方程组的系数矩阵十分特殊（被称为全单位模矩阵，其各阶非零子式均为 ±1），其非负可行解的分量只能取 0 或 1，故约束 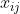= 0或1 可改写为 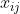≥ 0而不改变其解。此时，指派问题被转化为一个特殊的运输问题，其中 
，
。
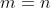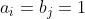3.2 求解指派问题的匈牙利算法
算法主要依据以下事实：如果系数矩阵 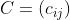一行（或一列）中每 一元素都加上或减去同一个数，得到一个新矩阵 
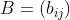，则以C 或 B 为系数矩阵的 指派问题具有相同的最优指派。
例 8 求解指派问题，其系数矩阵为
作业法解：
将第一行元素减去此行中的最小元素 15，同样，第二行元素减去 17，第三行 元素减去 17，最后一行的元素减去 16，得：
再将第 3 列元素各减去 1，得
以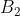
为系数矩阵的指派问题有最优指派
由等价性，它也是C 的最优指派。
python解：
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[16,15,19,22], [17,21,19,18], [24,22,18,17],[17,19,22,16]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind) # 开销矩阵对应的行索引
print('col_ind:', col_ind) # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素，形成数组
print('cost_sum:', cost[row_ind, col_ind].sum()) # 最小开销
输出结果：
row_ind: [0 1 2 3]
col_ind: [1 0 2 3]
cost: [15 17 18 16]
cost_sum: 66例 9 求解系数矩阵C 的指派问题
python实现：
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[12, 7, 9 ,7, 9],
[8, 9, 6, 6, 6],
[7, 17, 12, 14, 12],
[15,14, 6 ,6, 10],
[4,10 ,7 ,10 ,6]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind) # 开销矩阵对应的行索引
print('col_ind:', col_ind) # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素，形成数组
print('cost_sum:', cost[row_ind, col_ind].sum()) # 最小开销
输出结果：
row_ind: [0 1 2 3 4]
col_ind: [1 2 0 3 4]
cost: [7 6 7 6 6]
cost_sum: 32
4、对偶理论与灵敏度分析
4.1 原始问题和对偶问题
考虑下列一对线性规划模型：
（P）
和
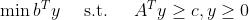（D）
称（P）为原始问题，（D）为它的对偶问题。
不太严谨地说，对偶问题可被看作是原始问题的“行列转置”：
（1） 原始问题中的第 j 列系数与其对偶问题中的第 j 行的系数相同；
（2） 原始目标函数的各个系数行与其对偶问题右侧的各常数列相同；
（3） 原始问题右侧的各常数列与其对偶目标函数的各个系数行相同；
（4） 在这一对问题中，不等式方向和优化方向相反。
考虑线性规划：
把其中的等式约束变成不等式约
Python小白的数学建模课-03.线性规划
-
线性规划是很多数模培训讲的第一个算法，算法很简单，思想很深刻。
-
要通过线性规划问题，理解如何学习数学建模、如何选择编程算法。
-
『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。
1. 求解方法、算法和编程方案
线性规划 （Linear Programming，LP） 是很多数模培训讲的第一个算法，算法很简单，思想很深刻。
线性规划问题是中学数学的内容，鸡兔同笼就是一个线性规划问题。数学规划的题目在高考中也经常出现，有直接给出线性约束条件求线性目标函数极值，有间接给出约束条件求线性目标函数极值，还有已知约束条件求非线性目标函数极值问题。
因此，线性规划在数学建模各类问题和算法中确实是比较简单的问题。下面我们通过这个比较简单、也比较熟悉的问题，分析一下数学模型问题的方法、算法和学习方案。探讨这些容易混淆的概念，也便于大家理解本系列教程的初衷和特色。
欢迎关注 『Python小白的数学建模课 @ Youcans』，每周更新数模笔记
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python数模笔记-PuLP库
Python数模笔记-StatsModels统计回归
Python数模笔记-Sklearn
Python数模笔记-NetworkX
Python数模笔记-模拟退火算法
1.1 线性规划问题的求解方法
解决线性规划问题有很多数学方法，例如：
- 图解法， 用几何作图的方法并求出其最优解，中学就讲过这种方法，在经济学研究中十分常用；
- 矩阵法， 引进松弛变量将线性规划问题转换成增广矩阵形式后逐次求解， 是单纯性法之前的典型方法；
- 单纯性法， 利用多面体在可行域内逐步构造新的顶点来不断逼近最优解，是线性规划研究的里程碑，至今仍然是最重要的方法之一；
- 内点法，通过选取可行域内部点沿下降方向不断迭代来达到最优解，是目前理论上最好的线性规划问题求解方法；
- 启发式方法，依靠经验准则不断迭代改进来搜索最优解 ，如贪心法、模拟退火、遗传算法、神经网络。
虽然不同的求解方法都是面对线性规划问题，也就必然会殊途同归，但它们在思想上就存在着本质区别，在求解方法和步骤上也就完全不同。
不夸张地说，对于很多小白，学没学过单纯性法，对于学习启发式方法可能完全没有区别。
这意味着什么呢？这就是说，对于非数学专业的同学，对于学习数学建模的同学，针对每一类问题，完全没必要学习各种解决方法。即便是数学专业的同学，也不可能在数模学习期间把各种方法都学会。
对于小白，本文推荐选择较为通用、相对简单（思路简单、程序简单）的方法来进行学习，没必要贪多求新。
1.2 线性规划的最快算法
算法，跟方法有什么不同呢？
算法的定义是“解题方案的准确而完整的描述”，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。
我对“方法”的理解是思想方法，是求解问题总体框架，而“算法”是具体和明确的实现步骤，在计算机编程中相当于详细的流程图。
在每一种方法的基本思想和方案提出后，往往都会有很多变形、改进和发展的算法。极少的改进算法具有实质贡献而成为主流的经典算法，即便如此往往也只是性能、效率上的提升，对于求解数模竞赛中的问题基本没有影响。
而绝大多数改进算法只是针对某些特殊情况、特殊问题（自称）有效，常用于大量的灌水论文。对于数学建模来说，学习基本算法或者目前的经典算法就足够了，不需要听信改进算法中自称的优点，那都是莆田系的广告。
有一种例外情况，就是一些算法是有适用范围和限制条件的。举个例子，内点法的基本算法不能处理等式约束，最短路径问题中 Dijkstar算法不能处理负权边。这种情况下如果选错算法，问题是无法求解的。所以对我们来说，搞清楚算法的适用范围，比理解算法本身更重要。
回到本节的标题，对于线性规划问题，什么算法是最快的呢？答案是：猜。不是让你猜，而是说求解线性规划问题，猜起来比较快。不是开玩笑，我是认真的。
佐治亚理工学院彭泱教授在 2021年计算机理论顶会 SODA2021 获得最佳论文（Best paper award at ACM-SIAM symposium on discrete algorithms 2021），正是研究线性规划问题的求解——“Solving sparse linear systems faster than matrix multiplication”，所用的全新思路是：猜，反复猜，迭代猜。
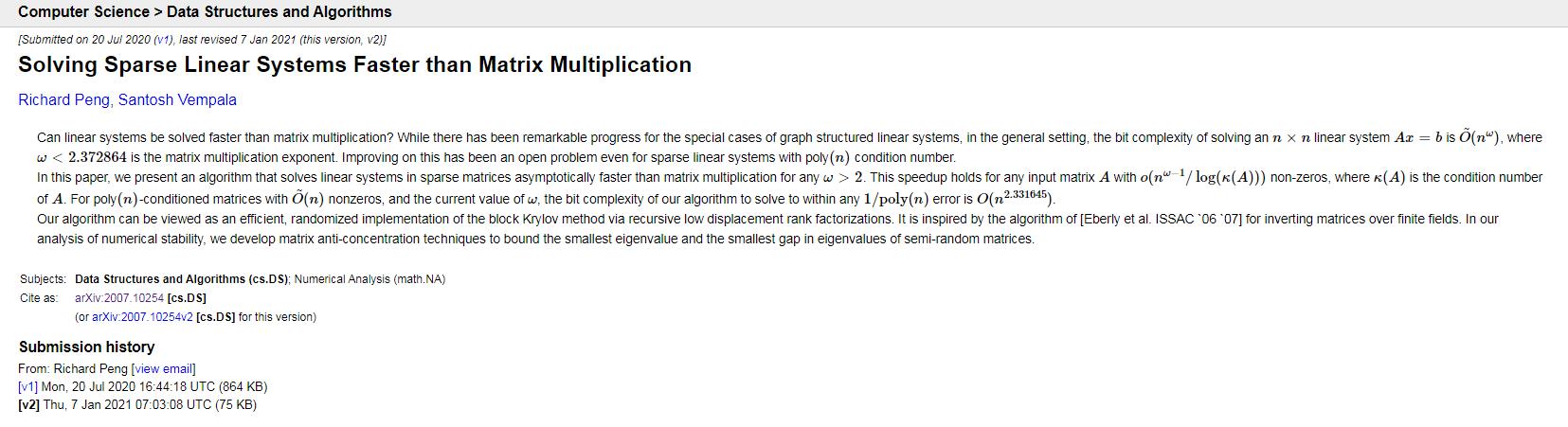
当然，猜起来比较快只是在某些特殊条件下才有效的，至于在什么条件下猜，怎么猜，这不是我们所要关心，所能理解的问题了。只是以此说明，简单的问题也有复杂的情况，每个问题都有很多求解的思路、方法和算法。
1.3 选择适合自己的编程方案
编程方案是我杜撰的术语。我所要表达意思是，在选择了求解方法和算法以后，是自己按照算法步骤一步步编程实现，或者找到例程调试使用，还是调用第三方工具包/库函数来完成呢？
首先，对于学习数学建模、参加数模竞赛，不建议自己按照算法步骤去编程。我们在《01.新手必读》中讨论过这个问题，对于数学小白兼计算机小白，这样做既不可行也没必要；即使你愿意挑战自我去试试，那其实已经是走在学习另一门计算机或算法课程的路上了。
其次，要不要找到例程自己调试、使用？很多数模培训就是这么说，这么做的，而且把这些收集的例程当作核心机密吸引同学。我不反对这样做，这种学习方法对于理解算法、提高编程能力很有帮助；但是并不推荐这样做，原因是：（1）我认为学习数学建模、参加数模竞赛，重点应该放在识别问题、分析问题、解决问题，能使用算法和编程就足够了；（2）第三方库与例程没有本质区别，第三方库就是经典的、规范的、标准化的例程，既然选择例程为什么不选择优秀的例程——第三方库呢？（3）大部分例程都存在很多问题，即使调试通过仍然有很多坑，而且新手难以识别。
所以我是明确推荐优选直接使用第三方库来解决问题，这也是 Python 语言“不要重复造轮子”的思想。
进一步地，很多工具包/库函数都能实现常用的算法，应该如何选择呢？
如果你对某个工具包已经很熟悉，又能实现所要的算法，这当然是理想的选择。如果你是小白，就跟着我走吧。
本系列选择第三方工具包的原则是：（1）优选常用的工具包；（2）优选通用功能的工具包和函数（例如，最好既能实现线性规划，又能实现整数规划、非线性规划）；（3）优选安装简单、使用简单、配置灵活的工具包；（4）优选兼模型检验、图形绘制的工具包。
2. PuLP库求解线性规划问题
2.1 线性规划问题的描述
线性规划是研究线性等式或不等式约束条件下求解线性目标函数的极值问题，常用于解决资源分配、生产调度和混合问题。
一般线性规划问题的标准形式为：
满足所有约束条件的解，称为线性规划问题的可行解；所有可行解构成的集合，称为可行域。
使目标函数达到最小值的解，称为最优解。
线性规划问题的建模和求解，通常按照以下步骤进行：
- 问题定义，确定决策变量、目标函数和约束条件；
- 模型构建，由问题描述建立数学方程，并转化为标准形式的数学模型；
- 模型求解，用标准模型的优化算法对模型求解，得到优化结果。
很多 Python 的第三方包，都提供求解线性规划问题的算法，有的工具包还提供整数规划、非线性规划的算法。例如：
- Scipy 库提供了解简单线性或非线性规划问题，但是不能求解如背包问题的0-1规划问题，或整数规划问题，混合整数规划问题。
- PuLP 可以求解线性规划、整数规划、0-1规划、混合整数规划问题，提供多种针对不同类型问题的求解器。
- Cvxpy 是一种凸优化工具包，可以求解线性规划、整数规划、0-1规划、混合整数规划、二次规划和几何规划问题。
此外，SKlearn、DOcplex、Pymprog 等很多第三方工具包也都能求解线性规划问题。
2.2 PuLP 求解线性规划问题的步骤
例题 1：
max fx = 2x1 + 3x2 - 5x3
s.t. x1 + 3x2 + x3 <= 12
2x1 - 5x2 + x3 >= 10
x1 + x2 + x3 = 7
x1, x2, x3 >=0
下面以该题为例讲解 PuLP 求解线性规划问题的步骤：
（0）导入 PuLP库函数
import pulp
（1）定义一个规划问题
MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize)
pulp.LpProblem 是定义问题的构造函数。
"LPProbDemo1"是用户定义的问题名（用于输出信息）。
参数 sense 用来指定求最小值/最大值问题，可选参数值：LpMinimize、LpMaximize 。本例 “sense=pulp.LpMaximize” 表示求目标函数的最大值。
（2）定义决策变量
x1 = pulp.LpVariable(\'x1\', lowBound=0, upBound=7, cat=\'Continuous\')
x2 = pulp.LpVariable(\'x2\', lowBound=0, upBound=7, cat=\'Continuous\')
x3 = pulp.LpVariable(\'x3\', lowBound=0, upBound=7, cat=\'Continuous\')
pulp.LpVariable 是定义决策变量的函数。
\'x1\' 是用户定义的变量名。
参数 lowBound、upBound 用来设定决策变量的下界、上界；可以不定义下界/上界，默认的下界/上界是负无穷/正无穷。本例中 x1,x2,x3 的取值区间为 [0,7]。
参数 cat 用来设定变量类型，可选参数值：\'Continuous\' 表示连续变量（默认值）、\' Integer \' 表示离散变量（用于整数规划问题）、\' Binary \' 表示0/1变量（用于0/1规划问题）。
（3）添加目标函数
MyProbLP += 2*x1 + 3*x2 - 5*x3 # 设置目标函数
添加目标函数使用 "问题名 += 目标函数式" 格式。
（4）添加约束条件
MyProbLP += (2*x1 - 5*x2 + x3 >= 10) # 不等式约束
MyProbLP += (x1 + 3*x2 + x3 <= 12) # 不等式约束
MyProbLP += (x1 + x2 + x3 == 7) # 等式约束
添加约束条件使用 "问题名 += 约束条件表达式" 格式。
约束条件可以是等式约束或不等式约束，不等式约束可以是 小于等于 或 大于等于，分别使用关键字">="、"<="和"=="。
（5）求解
MyProbLP.solve()
print("Status:", pulp.LpStatus[MyProbLP.status]) # 输出求解状态
for v in MyProbLP.variables():
print(v.name, "=", v.varValue) # 输出每个变量的最优值
print("F(x) = ", pulp.value(MyProbLP.objective)) #输出最优解的目标函数值
solve() 是求解函数。PuLP默认采用 CBC 求解器来求解优化问题，也可以调用其它的优化器来求解，如：GLPK，COIN CLP/CBC，CPLEX，和GUROBI，但需要另外安装。
2.3 Python例程：线性规划问题
例程 1：求解线性规划问题
# mathmodel04_v1.py
# Demo01 of mathematical modeling algorithm
# Solving linear programming with PuLP.
# Copyright 2021 Youcans, XUPT
# Crated：2021-05-28
import pulp
MyProbLP = pulp.LpProblem("LPProbDemo1", sense=pulp.LpMaximize) # 求最大值
x1 = pulp.LpVariable(\'x1\', lowBound=0, upBound=7, cat=\'Continuous\')
x2 = pulp.LpVariable(\'x2\', lowBound=0, upBound=7, cat=\'Continuous\')
x3 = pulp.LpVariable(\'x3\', lowBound=0, upBound=7, cat=\'Continuous\')
MyProbLP += 2*x1 + 3*x2 - 5*x3 # 设置目标函数
MyProbLP += (2*x1 - 5*x2 + x3 >= 10) # 不等式约束
MyProbLP += (x1 + 3*x2 + x3 <= 12) # 不等式约束
MyProbLP += (x1 + x2 + x3 == 7) # 等式约束
MyProbLP.solve() # youcans@xupt
print("Status:", pulp.LpStatus[MyProbLP.status]) # 输出求解状态
for v in MyProbLP.variables(): # youcans
print(v.name, "=", v.varValue) # 输出每个变量的最优值
print("Max F(x) = ", pulp.value(MyProbLP.objective)) #输出最优解的目标函数值
例程 1 运行结果：
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
Status: Optimal
x1 = 6.4285714
x2 = 0.57142857
x3 = 0.0
Max F(x) = 14.57142851
例程01 程序说明：
- 用 PuLP 库求解线性规划问题，可以选择求最大值或最小值，可以按照问题的数学描述，直接输入目标函数、等式约束和不等式约束，不等式约束可以选择 <= 或 >=，不需要进行转换。这中方式简单直观，非常适合初学者掌握。
- 对于较大规模线性规划问题， PuLP 库支持用字典类型（dict）建立多个变量，设置目标函数和约束条件。详见拙文《Python数模笔记-PuLP库（2）线性规划进阶》。
3. 小结
求解线性规划问题的方法非常简单，本文实际上并未讲解具体的算法。
希望通过对求解方法、算法和编程方案的讲解，阐明作者对于数学建模学什么、怎么学的理解，也使读者能了解本系列教程的特点：本教程不打算详细讲解各种算法的具体方法，重点介绍如何使用第三方包实现算法、解决问题。
【本节完】
版权说明：
欢迎关注『Python小白的数学建模课 @ Youcans』 原创作品
原创作品，转载必须标注原文链接。
Copyright 2021 Youcans, XUPT
Crated：2021-05-29
欢迎关注 『Python小白的数学建模课 @ Youcans』，每周更新数模笔记
Python小白的数学建模课-01.新手必读
Python小白的数学建模课-02.数据导入
Python小白的数学建模课-03.线性规划
Python数模笔记-PuLP库（1）线性规划入门
Python数模笔记-PuLP库（2）线性规划进阶
Python数模笔记-PuLP库（3）线性规划实例
Python数模笔记-StatsModels 统计回归（1）简介
Python数模笔记-StatsModels 统计回归（2）线性回归
Python数模笔记-StatsModels 统计回归（3）模型数据的准备
Python数模笔记-StatsModels 统计回归（4）可视化
Python数模笔记-Sklearn （1）介绍
Python数模笔记-Sklearn （2）聚类分析
Python数模笔记-Sklearn （3）主成分分析
Python数模笔记-Sklearn （4）线性回归
Python数模笔记-Sklearn （5）支持向量机
Python数模笔记-NetworkX（1）图的操作
Python数模笔记-NetworkX（2）最短路径
Python数模笔记-NetworkX（3）条件最短路径
Python数模笔记-NetworkX（4）最小生成树
Python数模笔记-NetworkX（5）关键路径法
Python数模笔记-模拟退火算法（1）多变量函数优化
Python数模笔记-模拟退火算法（2）约束条件的处理
Python数模笔记-模拟退火算法（3）整数规划问题
Python数模笔记-模拟退火算法（4）旅行商问题
以上是关于Python数学建模—线性规划的主要内容，如果未能解决你的问题，请参考以下文章