公钥私钥对称加密非对称加密混合加密摘要签名证书及CA
Posted RickChandler
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了公钥私钥对称加密非对称加密混合加密摘要签名证书及CA相关的知识,希望对你有一定的参考价值。
目录
2.对称加密(Symmetric Key Encryption)
3.非对称加密(Asymmetric Key Encryption)
7.摘要算法(Digest Algorithm)及数据的完整性
10.数字证书(Public Key Certificate,PKC)及证书认证机构(Certification Authority,CA)
1.数据机密性
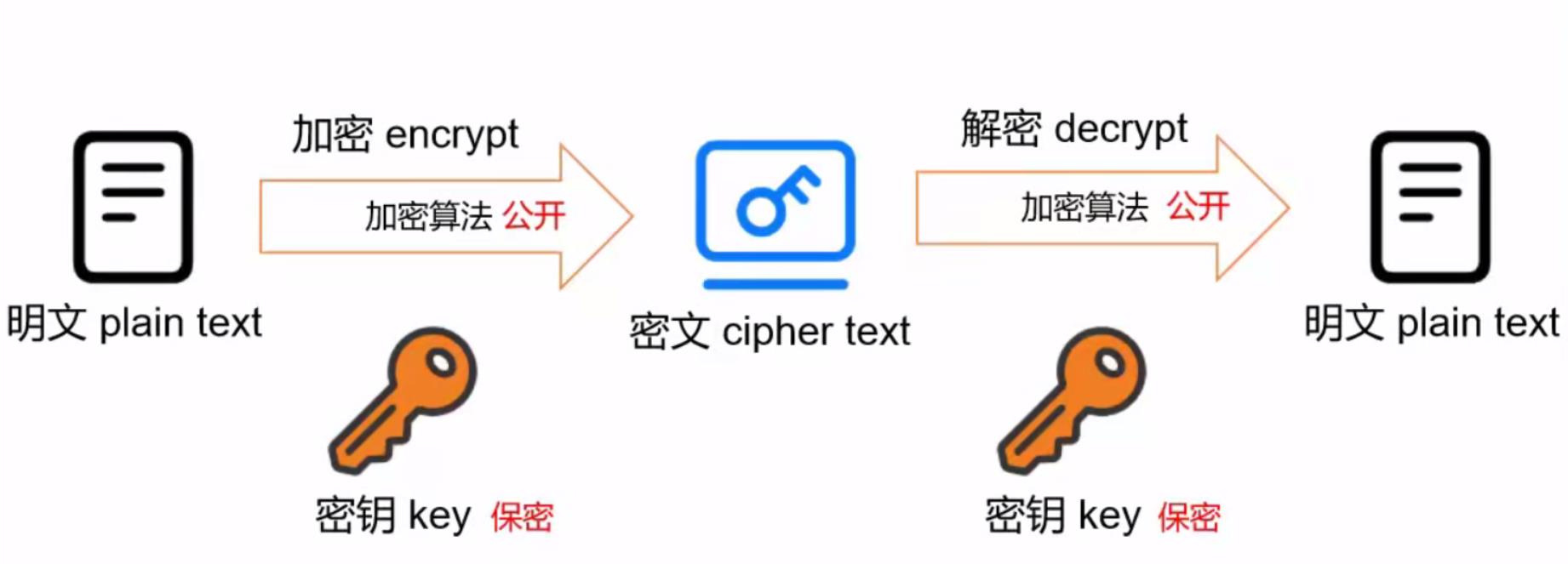
我们用上面这个图来聊聊数据机密性实现的方式,首先解释一些名词。
- 明文(Palin Text):加密前或解密后的数据我们称其为明文。
- 密文(Cipher Text):加密后的数据我们称其为密文。
- 密钥(Key):只有拥有”钥匙“的人才能获取之前锁起来的东西,所以这个”钥匙“指的就是密钥,用来解密之前加密形成的明文。密钥是需要保密的,如果泄露后,任何人都可以还原密文为原文,加密将失去意义。密钥的度量单位是位 Bit,例如秘钥长度128,就是16字节的二进制串。
- 加密(Encrypt):实现数据机密性的最常用手段就是对数据进行加密,按照秘钥的使用方式,加密可以分为两大类,就是对称加密(Symmetric Encryption)和非对称加密(Asymmetric Encryption)。
- 解密(Decrypt):使用秘钥将密文还原为明文的过程我们称其为解密。
- 加密算法(Encryption Algorithm):主要是指我们加密的方式,就是说将明文按照某种算法进行处理,将其变成不可读的密文,只有拿对应的密钥才可以还原,因此加密和解密过程中都会用到加密算法。加密算法是公开的,常见的有DES,3DES,RC2,RC4,IDEA,RSA,AES,BLOWFISH,MD5,PKCS,SSF33,SSF28,SCB2(SM1)等。
2.对称加密(Symmetric Key Encryption)

所谓对称加密就是指对数据进行加密和解密时所使用的密钥是同一个,所谓对称的,所以也称这种加密方式为单密钥加密。
最常见的对称加密算法是AES(Advanced Encryption Standard,高级加密标准)加密算法,又称Rijndael加密算法,是美国联邦政府采用的一种区块加密标准,密钥长度是128、192或者256,安全强度很高且性能很好,替代了原先的DES(Data Encryption Standard,数据加密标准)加密算法。
还有一种改进后的对称加密算法,就是不再将明文当做一整个数据进行加密,而是将其分成很多的数据块进行分块加密,就是所谓的分组加密,也叫块加密(Block Cyphers),常见的算法模式有ECB、CBC、PCBC、CFB、OFB、CTR等,微信支付中使用的是AEAD_AES_256_GCM。
3.非对称加密(Asymmetric Key Encryption)
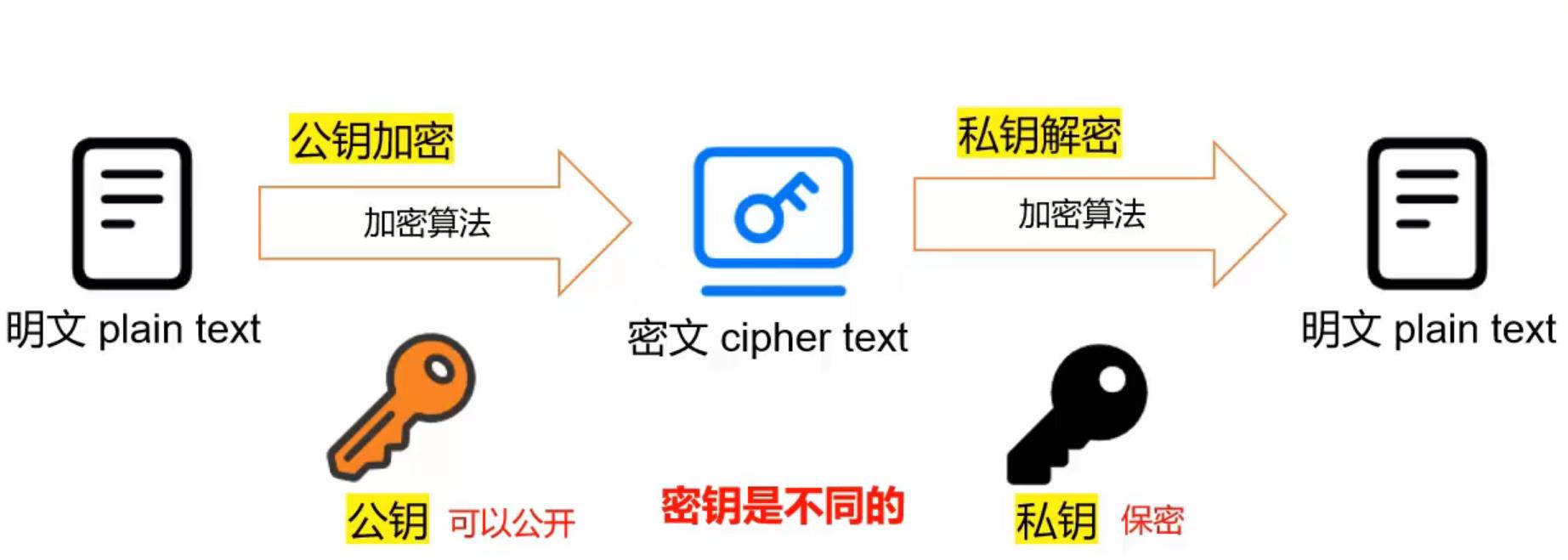
从上面的对称加密(单密钥加密)定义就可以理解为什么会有非对称加密,就是说非对称加密有两个密钥,且是不同的,即不对称的,你也可以叫它”双密钥加密“。它的两个密钥一个叫公钥(Public Key),一个叫私钥(Private Key)。使用公钥加密后只能用私钥解密,反之,私钥加密后也只能用公钥解密。至于公钥加密和私钥加密的区别和目的,后面讲述身份认证时会进行详细的说明。
常见的非对称加密算法有RSA、DSA、ECC、DH,其中RSA加密算法是最著名的也是应用最广发的非对称加密算法。
4.对称加密与非对称加密的对比
- 对称加密
- 优点:运算速度非常快。
- 缺点:虽然对称加密的运算速度非常快,但是他有一个很大的问题,那就是密钥的安全性。因为秘钥需要数据交换双方的共享,也就是说要持有同一个密钥,也就是说数据传输的过程要对密钥进行传输,所以数据传输的过程中密钥一旦被窃取,数据就会被破解,通讯过程当然就没有机密性可言。
- 非对称加密
- 优点:保密性好。私钥严格的保密,公钥可以任意分发,即使公钥被窃取,仍然无法破解加密后的信息。
- 缺点:运算速度非常慢。它这个速度慢的原因是它基于很复杂的数学算法才得以实现它的安全性,慢到什么程度呢?这么说吧,就因为它的计算速度非常慢,从而导致它无法保证通讯的速度,极端情况下比对称加密慢1000倍,自然就无法取代对称加密的地位,所以并没有出现摒弃对称加密而全部使用非对称加密的局面。
5.混合加密(Hybrid Key Encryption)
一般情况下要保证数据的安全性和加解密的效率,都是对称加密和非对称加密结合使用的,称之为混合加密。例如,我们可以先产生一个随机数,也就是所谓的会话密钥(Session Key),作为对称加密的密钥,用来加密数据。然后用非对称加密方式的公钥加密会话密钥,因为会话密钥很短,通常只有 16 字节或 32 字节,所以慢一点也无所谓。对方拿到密文(非对称加密后的会话密钥)后用私钥解密,取出会话密钥。这样,双方就实现了对称密钥的安全交换,后续就不再使用非对称加密,全都使用对称加密发送数据。这样做就可以先保证密钥传输的安全性,再间接的保证通讯的安全性,即可以保证密钥传输的安全性,同时也可以保证后续数据传输过程中加解密的效率,因为我们只需要用非对称加密方式来加密会话密钥,而数据的加密则使用对称加密的方式。我们所熟知的HTTPS协议的底层原理,其实使用的就是这个原理。

6.身份认证

关于身份认证,首先是针对非对称加密来讲的,就是说我们拥有两个密钥,一个是公钥,一个是私钥。
如上图所示,Bob拥有自己的一对密钥,分别为私钥和公钥,他把自己的公钥发给了任何他想与之交换信息的一方,例如上图中的Pat、Doug和Susan,用于解密Bob发给他们的信息,通讯流程如下图所示。

首先Susan如果要写信息给Bob的话,要用Bob发给她的公钥将明文加密为密文后发送,当Bob收到密文信息后,使用自己的私钥将信息解密后即可得到信息明文。

然后,如上图所示,当Bob要给Susan回信的时候,就要使用Susan发给大家的公钥,所以Bob用Susan的公钥将明文加密为密文后发送给Susan,Susan收到信息密文后,使用自己的秘钥将密文解密后便可得到信息明文。
以上逻辑貌似没有问题,但是其实存在问题的。比如Susan给Bob写信的时候以及Bob给Susan回信的时候,对方怎么知道发送信息的人就是正确的呢?因为Susan发信息时使用的是Bob的公钥进行加密的明文,同样Bob回信的时候也是使用的Susan的公钥进行加密的明文。也就是说如果彼此都用对方的公钥进行加密明文,这样子是无法确认发送方的身份的,也就是无法进行身份认证。
那这个问题怎么解决呢?我们看看下面这个流程。

首先,Bob给它的朋友们发信的时候不再使用对方的公钥加密明文,而是使用自己的私钥加密明文,然后收信息的人用Bob的公钥进行解密,那这样的话有什么不同呢?

首先,我们以Bob发送信息给Susan为例。我们知道的是,Bob只把自己的公钥发给了他的朋友们,所以私钥只有Bob才有。因此当Bob用自己的私钥加密明文发送信息给他的朋友们时,他的朋友们就可以确认这个信息就是Bob发出来的,因为私钥只有Bob自己有,除非Bob的私钥泄露了。因此,当Bob的朋友们收到信后,用Bob的公钥进行解密得到明文,即可获取确保是Bob发出的信息。同理,当Bob的朋友们回信的时候,也使用他们自己的私钥进行加密明文,当Bob收到加密后的密文信息后,使用他的朋友们发给他的各自的公钥对密文进行解密的得到明文,Bob即可获取确保是他的朋友们发送给他的信息。
至此,我们就可以发现,使用公钥加密和使用私钥加密的区别所在:
- 公钥加密,私钥解密的作用是加密信息。因为只有拥有私钥的人才可以获取信息明文。
- 私钥加密,公钥解密的作用是身份认证。因为只有拥有私钥的人才可以发送信息密文。
7.摘要算法(Digest Algorithm)及数据的完整性
我们先讨论为什么会有摘要算法这个东西,也就是某一项技术出现的业务场景。我们要知道的是,需要发送的信息主体肯定不能用非对称加密,之前描述对称加密和非对称加密时有提起过,因为非对称加密计算的复杂性,导致其非常的耗时,所以实际使用中大都是混合加密,例如HTTPS协议底层的的SSL协议通信。那么在混合加密的方式中,信息的加密方式是对称加密,既然是对称加密,所以就存在密钥被拦截,从而解密获取明文,进而篡改原文,重新加密,然后再转发给收信方。这样的信息经过了篡改破坏,从而就无法保证原始信息的完整性。
那这个问题怎么解决呢?
目前,保证信息完整性的手段主要就是摘要算法(Digest Algorithm),所谓的摘要(Digest )就是对发送的信息按照一定的算法进行“压缩”,使其产生一个独一无二的固定长度的字符串,就像是给这个信息生成了一个数字“指纹”,我们称为摘要(Digest ),用它来保证数据的完整性。产生摘要所使用的算法也就称为摘要算法,它就是我们常说的散列函数、哈希函数(Hash Function)。

摘要算法主要有以下特性:
- 不可逆性:只有算法,没有密钥,只能加密,不能解密。所以摘要的比对只有拿到信息后用同一种摘要算法重新生成摘要,然后和信息携带的摘要进行比对,两个摘要一致则数据具有完整性,反之则被篡改过,破坏了完整性。
- 难题友好性:摘要是很难破解的,只有暴力枚举。也就是说你只有穷举所有字符串产生的摘要与要破解的摘要进行比对,相等了则被破解,反之,则继续穷举。
- 发散性:只要对原文进行一点点改动,摘要就会发生剧烈变化,也称之为“雪崩效应”。
- 抗碰撞性:原文不同,计算后的摘要也要不同。因为原始信息的长度是未知的,但是摘要的长度是固定的,我们可以理解为生成摘要是将一个“大空间”映射到一个“小空间”,因此就会有可能产生“大空间”不同的点对应“小空间”的同一个点,我们就称这种现象为“碰撞”。我们所需要的“抗碰撞性”,就是尽量避免这种情况的发生。用数学来描述就是我们需要让这个函数F(x->y)既是是单射函数,又是满射函数,使其值域和定义域是一一映射的(双射)。
常见的摘要算法主要有:MD5(Message Digest Algorithm 5)、SHA1(Security Hash Algorithm 1)、SHA2(Security Hash Algorithm 2)包含SHA224、SHA256、SHA384。

接下来,我们通过上面这张图来梳理一下对信息用摘要来保证它完整性的流程。同样,我们使用Bob发信作为例子。比如Bob要发信息给他的好友Pat,为了防止原文被拦截篡改,他首先对信息全文用摘要算法生成摘要,然后附带在原文的下面,之后发送出去了。过了几秒钟,Pat收到Bob的信息,他首先取出来信息中附带的摘要,然后使用和Bob相同的摘要算法对得到的信息计算生成另一个摘要,再拿着信息原来附带的摘要与自己生成的摘要进行比对,如果相同,则信息完整性未被破坏,反之则被篡改过,破坏了完整性。
这样貌似很完美,但还是有问题,首先摘要算法是公开的,且如果消息被拦截,其他人篡改原文之后,使用同样的摘要算法生成消息摘要,附带在消息下边,然后转发给收信人,这样收信人是无法判断消息的完整性的。那么如何解决这个问题呢?那就需要下面描述的数字签名了,因为这正是数字签名的应用场景,也是它需要解决的问题。
8.数字签名(Signature)
刚才有说到简单的只用摘要来保证信息的完整性是存在风险的,并不可靠,所以就有了数字签名的存在。那什么是数字签名呢?
首先,我们可以分析一下刚才那种风险出现的原因及它的致命点在哪里?
我们的消息接收方是通过比对摘要来判断消息是否具有完整性,篡改消息者也是篡改了消息原文之后,还需要用同样的摘要算法重新生成摘要,使得篡改后的消息和消息的摘要对应得上,那么这个风险出现主要原因并不是消息被拦截,而是我们的摘要被替换了,所以它的致命点就在于摘要的获取上。
因此,我们只要使得摘要不可被获取且让摘要具有身份认证,不就可以防止摘要被替换了吗?没错,事实也是如此,就是采用了这个方案去解决这类风险的。那么具体是怎么实现的呢?
首先,我们要实现摘要的不可获取。这还不容易嘛,今天我们聊的就是加密呀,保证摘要的机密性不就好了,摘要也是属于信息的,所以实现摘要的不可获取直接将它加密传输就好了。其次,既然要加密摘要的话,我们应该选择那种加密方式呢?加密方式的选择就和它的另一个要求有关系了,那就是还需要具有身份认证。还记得我们之前聊非对称加密的公钥加密和私钥加密的区别吗?我们说公钥加密的作用是加密,私钥加密的作用是身份认证。所以这里就采用非对称加密的私钥来加密摘要生成密文,摘要加密后的密文,我们称之为数字签名(Signature),因为他代表发信人的身份以及摘要生成人的身份,所以称为签名。
使用数字签名的流程如下图所示:
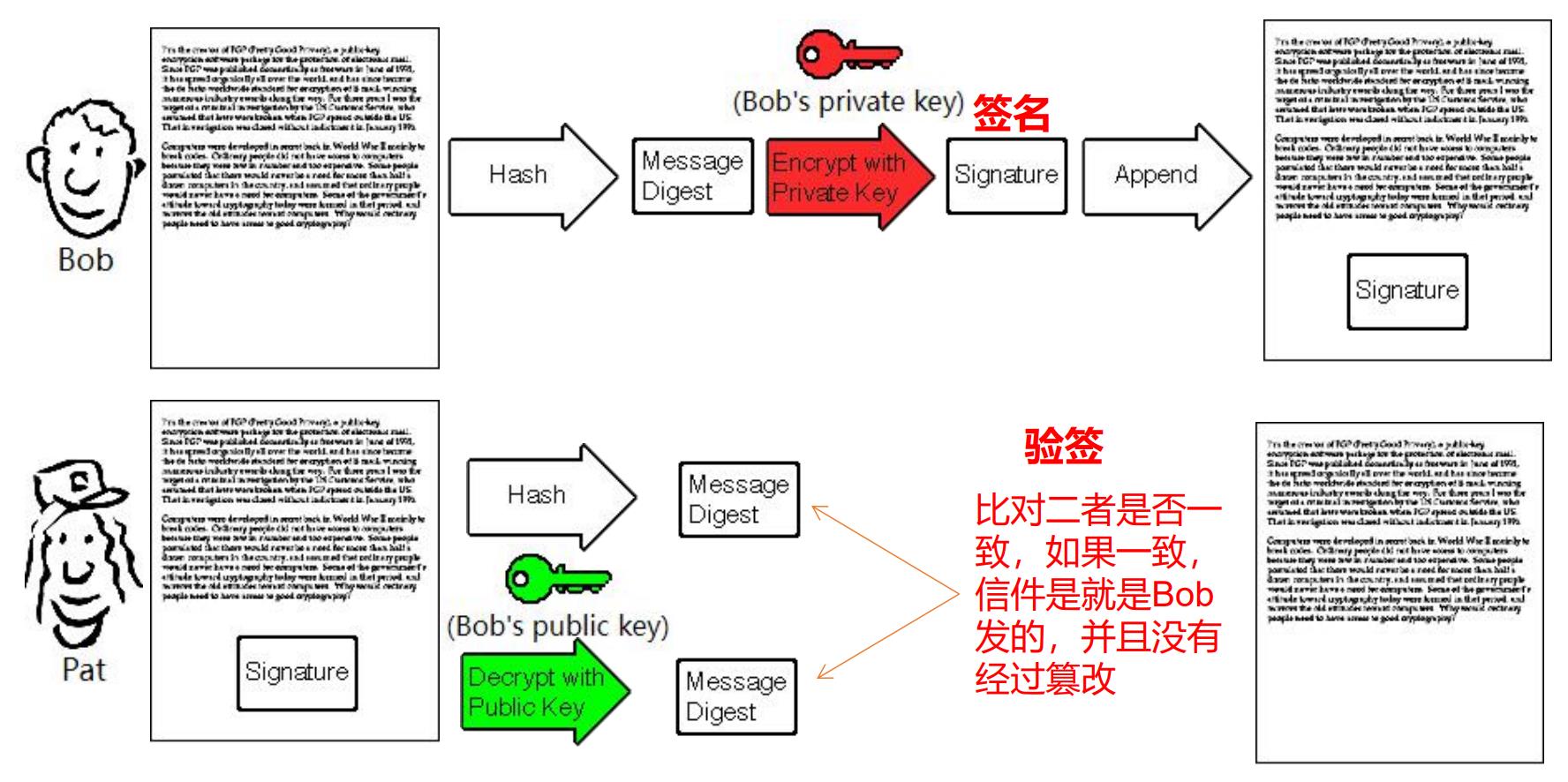
我们还是以Bob和Pat为例子。当Bob要给Pat发信时,首先对消息原文使用摘要算法生成摘要,然后Bob使用自己的私钥对摘要进行加密,生成数字签名,这个过程我们也可称之为加签(附加数字签名),最后将数字签名附带在消息的下边一起发送给Pat。几秒钟后,Pat收到信息,首先用Bob的公钥解密数字签名,得到明文,也就是摘要(签名就是摘要加密生成的),然后再对消息使用和Bob一样的摘要算法生成另一个摘要,最后Pat将签名解密得到的摘要和自己生成的摘要进行比对,这个过程我们也可称之为验签(校验数字签名),如果一致,则消息就是Bob发出的且没有被篡改的,保证了消息的完整性,反之,则消息未必是Bob发出的且消息的完整性被破坏。
9.数字签名结合对称加密原文
回想一下,我们刚刚是不是忘记了一件事?我只想着保证消息的完整性,以及摘要的安全性,但是消息本身并没有加密呀,所以应该加密一下原文,保证消息原文的机密性,之前我们说过对称加密和非对称加密方式的区别,这里就不赘述了,为了消息加解密的效率,这里肯定是选择对称加密的方式,然后结合数字签名来实现消息的机密性和完整性。
主要流程如下图所示:

从上图可以看出来,其实只是在加签和验签的基础上,多了一步对消息的对称加解密。加密和解密都是在加签和验签之后进行的。
至此,我们为了保证消息的机密和完整性采用了混合加密、生成摘要、加密摘要生成签名一些列手段,这样就真的安全了吗?其实并不见得,我们逐渐忽略了最基本的安全问题,就是密钥的安全。之前我们说过公钥是可以任意分发的,同样也会出现伪造的公钥,那么如何确保公钥的正确性和可信性呢?
要解决上面的问题,数字证书和证书认证机构的存在便有了意义,下面我们就来聊聊PKC和CA。
10.数字证书(Public Key Certificate,PKC)及证书认证机构(Certification Authority,CA)
首先,我们来聊聊他们的名称及基本概念。
数字证书(Public Key Certificate,PKC),虽然我习惯叫它”证书“,但是我们从它的英文名称可以看出来它原来的全称叫做“公钥证书”,这就好理解了,它的存在其实就是为了用来证明公钥的可靠性,其实它就像我们的”身份证“一样,既可以证明我们身份的真实可靠,也具有防伪的功能及权威性。
刚刚有提到权威性,那么如何保证证书本身的真实性呢?于是便有了证书认证机构(CA)的概念。
证书认证机构(Certification Authority,CA),顾名思义,这就是认证且颁发证书的机构。刚刚在描述证书的时候用我们的身份证来做了个比喻,接着用这个例子的话,那证书认证机构就相当于“公安局”,这个机构具有一定的权威性和可靠性,因此进而保证了证书的可靠性,最终就可以最大限度的实现公钥的真实可靠。
接下来,我们用一个例子来说明PKC及CA存在的必要性。如下图所示:

假如说哈,Doug拿着一个公钥发给了Pat,谎称这是Bob的公钥,然后Doug用自己的私钥给消息加上签名,然后发给了Pat,几秒钟后Pat收到消息,用之前拿到的公钥进行验签,然后获取消息。这个过程中Pat会一直以为是Bob在和他通信,谁知一开始的公钥就是错的,是Doug全程在和他交换消息。所以就导致了这个问题,这也是为什么需要PKC和CA的原因。
接下来,我们来仔细聊一下证书里边的一些东西,就是它到底包含了那些东西。
证书主要包含以下几个重要信息(以Bob为例):
- 公钥:就是需要被认证的公钥(Bob的公钥)。
- 所有者:就是公钥的所有者(Bob)。
- 颁发者:CA(Certification Authority,证书认证机构)。
- 有效期:证书的使用期限。
- 摘要算法:指定生成摘要的哈希算法,用来计算证书的摘要,因为证书也要保证自己本身的完整性。
- 指纹:证书的摘要。
- 签名算法:指定生成签名的算法,用于计算证书的数字签名,确保证书是由CA签发。
- 签名:证书的数字签名,CA(证书认证机构)用自己的私钥给这个证书生成的数字签名。
- 序列号:证书的唯一标识。
了解完上述几个PKC中的概念,我们来看一下PKC生成的过程,如下图所示:

还是以Bob为例子。首先Bob要做的第一件事当然是登记信息,比如自己的身份、要发布的公钥、还有证书的用途等等,然后CA确认信息且登记后,通过哈希算法生成这些信息的摘要,CA再用自己的私钥生成证书的数字签名,将签名附加在证书信息下边,最后就生成了一个具有可靠性和完整性的证书。
至此,使用者拿到证书后就可以获取到一个安全可信的公钥了,如下图所示,Bob再发送消息给Pat时,在消息下附加上自己的证书即可。

我们来了解一下带有证书后消息的完整发送及接收过程,如下图所示:

首先呢,Bob对自己要发送的信息计算摘要、计算签名,然后在消息的下边附带上自己证书一起发送给Pat。几秒钟后Pat收到信息,要做的第一件事就是取出消息附带的证书,使用CA公钥对其进行验签,确保证书的可靠性,验签后就得到了证书的摘要,也就是证书指纹,然后使用指定的摘要算法对证书信息进行计算生成摘要,比对两个摘要是否一致,确保证书的完整性。之后就可以核实证书中的信息,比如公钥所有者是否正确、证书是否有效、证书是否为权威CA签发等等。确认无误后,就可以拿出证书中的公钥了。然后,再用这个公钥对收到的消息进行验签,保证可靠性,其次对消息内容计算摘要,比对摘要是否一致,保证消息的完整性,最终就可以阅读消息了。
如此一来,有了上述的过程,就最大限度实现了既可以保证公钥的可靠性和完整性,同时也保证了消息本身的可靠性和完整性。
可这样就完了吗?就绝对安全了吗?当然不是,因为这个世界上”绝对“的事情少之又少,可以当做不存在。所以,就在这里留下一个问题哈,你们自行了解,我就不深入了。
问题就是:刚刚我们拿到证书后,校验了证书上的数字签名,我们使用的是CA的公钥,那么这个公钥是可靠的吗?
11.HTTPS协议中数字证书的应用
这是一个证书在实际应用中的典型例子,就是HTTPS协议是如何实现安全可靠的。
我大概说一下流程,就不赘述了,上面说混合加密的时候提过一嘴。
主要分为两部分:
- 网站向CA申请数字证书-->CA颁发数字证书-->网站得到数字证书-->变成HTTPS网站(安全的)
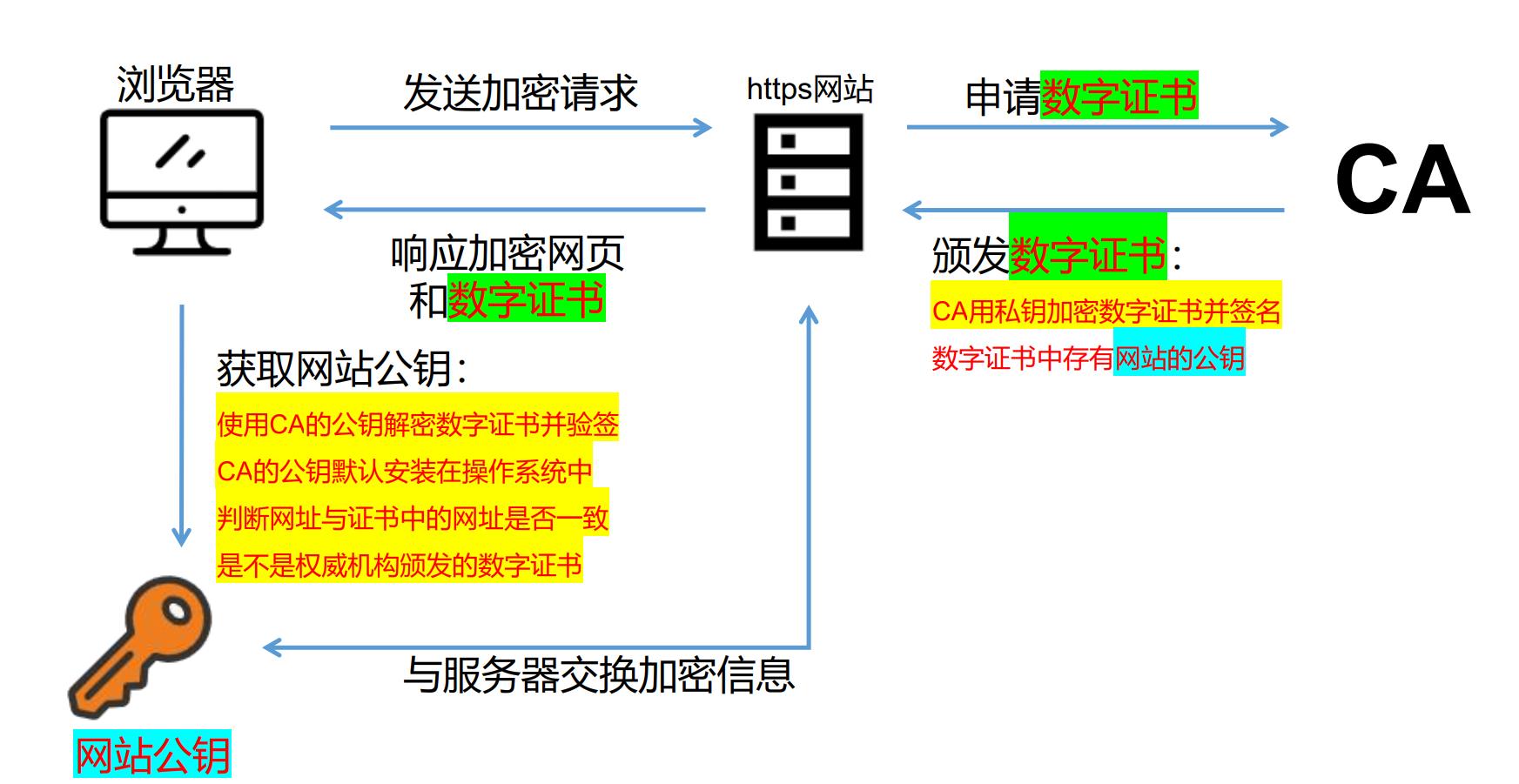
- 浏览器发起加密请求-->HTTPS网站响应加密网页和数字证书-->浏览器校验数字证书-->获取网站公钥-->开始交换加密信息
流程如下图所示:
以上是关于公钥私钥对称加密非对称加密混合加密摘要签名证书及CA的主要内容,如果未能解决你的问题,请参考以下文章