leetcode解题笔记--part1--array
Posted Lainey❤
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode解题笔记--part1--array相关的知识,希望对你有一定的参考价值。
目录
18. 4Sum ★★
33. Search in Rotated Sorted Array ★
78. Subsets ★★
80. Remove Duplicates from Sorted Array II
81. Search in Rotated Sorted Array II ★
105. Construct Binary Tree from Preorder and Inorder Traversal ★★
106. Construct Binary Tree from Inorder and Postorder Traversal
152. Maximum Product Subarray ★★
153. Find Minimum in Rotated Sorted Array ★
209. Minimum Size Subarray Sum ★★
238. Product of Array Except Self ★
287. Find the Duplicate Number ★★
380. Insert Delete GetRandom O(1) ★
442. Find All Duplicates in an Array ★★
713. Subarray Product Less Than K ★
714. Best Time to Buy and Sell Stock with Transaction Fee ★★★
718. Maximum Length of Repeated Subarray
11.Container With Most Water【Medium】 返回目录
题目:
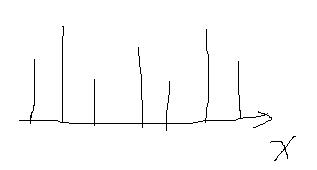

解题思路:
没有叫你返回具体坐标,只要求最大面积的话,那么用一个变量记录下,然后两边开始往中间移动
对于长边来讲,往里边移动一个坐标,无论更长或者更短,都不会使面积变大,所以每次都移动短边,这样每移动一次,最大面积都有可能更新
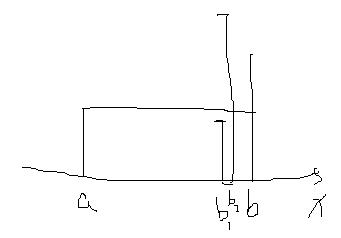
Tip:如果不采用两边移动的话,就是要进行两两遍历,也就是O(n2), 两边移动就是O(n)
code:
1 def maxArea(self, height): 2 """ 3 :type height: List[int] 4 :rtype: int 5 """ 6 i = 0 7 j = len(height)-1 8 maxarea = 0 9 while i < j: 10 maxarea = max((j-i)*min(height[i],height[j]), maxarea) 11 if height[i] < height[j]: 12 i += 1 13 else: 14 j -= 1 15 return maxarea
15. 3Sum【Medium】 返回目录
题目:
Given an array S of n integers, are there elements a, b, c in S such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero
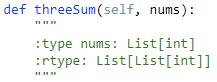
解题思路:
做2Sum的时候用的是hash算法O(N)就可以做完,那么这个3Sum其实就是一个O(N)的2Sum, 于是乎就是O(N*N)的算法
2Sum算法如下:O(N)
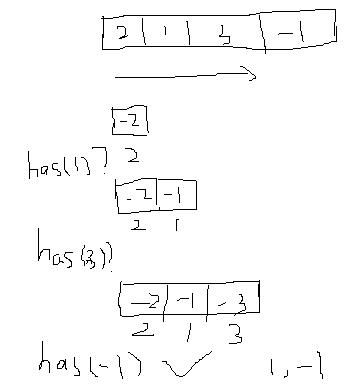
所以3Sum只需进行O(N)次2Sum就行了,写个循环完成
Tip:数组题要是涉及到找数字,记得用hash法,用空间换时间
code:
1 def threeSum(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 length = len(nums) 7 if length < 3: 8 return [] 9 result = [] 10 nums.sort() 11 for i in range(length-2): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 hash_table = {} 15 res = 0-nums[i] 16 for j in range(i+1,len(nums)): 17 if j>3 and nums[j]==nums[j-3]: 18 continue 19 if nums[j] in hash_table: 20 result.append([nums[i],res-nums[j],nums[j]]) 21 hash_table.pop(nums[j]) 22 else: 23 hash_table[res-nums[j]] = nums[j] 24 return result
哇,这道题处理重复很头疼啊,对于[1,0,-1,1]结果为[[1,0,-1],[0,-1,1]]显示说答案错误
如果找到一组解的时候,在result里面查询是否已经存在的话就会多一层循环,结果会超时。
所以这里预先将数组进行排序,让可行的结果呈顺序状,更好地防止结果重复。
但是面对大量重复数字的时候,出现很多问题, 比如[0,0,0,0,0,0,0,0,0,0,0,0], [-4,2,2,2,2,2,2,2,3]
这里就要求固定第一个数字的时候,希望不重复,也就是要跳过nums[i]==nums[i-1]的情况
对于第二个数字呢,因为只要求2sum,所以对于重复大于3的情况不需要考虑。即跳过nums[j]==nums[j-3]
很奇怪为什么我的算法ac时间很长,统计数据只打败了2.9%提交的python代码,看下别人的解法
code_writen_by_others:
1 def threeSum(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: List[List[int]] 5 """ 6 length = len(nums) 7 if length < 3: 8 return [] 9 result = [] 10 nums.sort() 11 for i in range(length-2): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 res = 0 - nums[i] 15 low = i+1 16 high = length-1 17 while(low < high): 18 if(nums[low]+nums[high]==res): 19 result.append([nums[i],nums[low],nums[high]]) 20 while(low<high and nums[low]==nums[low+1]): 21 low += 1 22 while(low<high and nums[high]==nums[high-1]): 23 high -= 1 24 low +=1 25 high -=1 26 else: 27 if(nums[low]+nums[high]<res): 28 low += 1 29 else: 30 high -= 1 31 return result
我好笨啊,因为已经排好序了,所以没必要用hash,直接两头做加法往中间移动,比hash省了空间还省了时间
但是2Sum用hash更好,因为排序算法是O(NlogN)的,hash是O(N)的,所以追求效率的话还是hash
16. 3Sum Closest【Medium】 返回目录
题目:

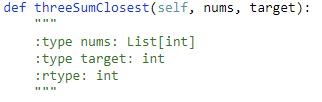
解题思路:
与15题类似,只不过需要一个额外的哨兵记录下与目标的差异,遍历完留下差异最小的值
同时在遍历的过程中,如果比target要更大,需要移动更大的数变小,如果比target更小,需要移动更小的数变大
Tips:如果算法的时间复杂度为O(N*N), 那么最好事先就先排序,排好序之后就没有必要hash了,本来两头遍历复杂度也为O(N)
code:
1 def threeSumClosest(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 nums.sort() 8 min_diff = float("inf") 9 for i in range(len(nums)): 10 res = target-nums[i] 11 low,high = i+1,len(nums)-1 12 while low < high: 13 diff = nums[low]+nums[high]-res 14 if diff == 0: 15 return target 16 if abs(diff) < min_diff: 17 min_diff = abs(diff) 18 result = nums[i]+nums[low]+nums[high] 19 if diff > 0: 20 high -= 1 21 else: 22 low += 1 23 return result
18. 4Sum【Medium】 返回目录
题目:

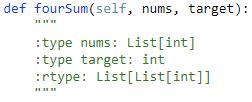
解题思路:
在网上看了一个特别brilliant的解法,让人觉得代码很有美感,而且还非常高效,就是把所有不需要的测试全部略过,让人赞叹不已
而且这道题还结合了前几道题的操作,这道题必须mark上两颗星
Tips:去除一些不必要的操作,虽然时间复杂度没有变,但是实际运行时间是减少的
code:
1 def fourSum(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 nums.sort() 8 res = [] 9 if len(nums)<4 or 4*nums[0]>target or 4*nums[-1]<target: 10 return res 11 for i in range(len(nums)): 12 if i>0 and nums[i]==nums[i-1]: 13 continue 14 if nums[i] + 3*nums[-1] < target: 15 continue 16 if 4*nums[i] > target: 17 break 18 if 4*nums[i] == target: 19 if i+3<len(nums) and nums[i+3]==nums[i]: 20 res.append([nums[i],nums[i],nums[i],nums[i]]) 21 break 22 res.extend(self.threeSum(nums[i+1:],target-nums[i],nums[i])) 23 return res 24 25 def threeSum(self,nums,target,a): 26 res = [] 27 if len(nums)<3 or 3*nums[0]>target or 3*nums[-1]<target: 28 return res 29 for i in range(len(nums)): 30 if i>0 and nums[i]==nums[i-1]: 31 continue 32 if nums[i] + 2*nums[-1] < target: 33 continue 34 if 3*nums[i] > target: 35 break 36 if 3*nums[i] == target: 37 if i+2<len(nums) and nums[i+2] == nums[i]: 38 res.append([a,nums[i],nums[i],nums[i]]) 39 break 40 res.extend(self.twoSum(nums[i+1:],target-nums[i],a,nums[i])) 41 return res 42 43 def twoSum(self,nums,target,a,b): 44 res = [] 45 if len(nums)<2 or 2*nums[0]>target or 2*nums[-1]<target: 46 return res 47 i,j = 0,len(nums)-1 48 while i<j: 49 sum_temp = nums[i]+nums[j] 50 if sum_temp == target: 51 res.append([a,b,nums[i],nums[j]]) 52 i += 1 53 j -= 1 54 elif sum_temp > target: 55 j -= 1 56 else: 57 i += 1 58 while i>0 and i<len(nums) and nums[i]==nums[i-1]: 59 i += 1 60 while j>0 and j<len(nums)-1 and nums[j]==nums[j+1]: 61 j -= 1 62 return res
31. Next Permutation【Medium】 返回目录
题目:
给你一个排列,要你求出,作为全排列组合中它的下一个排列。一般都是指一个升序数列的全排列An^n个,比如说:
[1,2,3] --> [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] --> [1,2,3]
本题要求:找到给出排列的下一个排列


解题思路:
观察找到全排列的规律,发现是个多重循环,按位置从小到大,可以得到的规律如下:【借鉴别人给出的例子,侵删】
1 2 7 4 3 1 --> 1 3 1 2 4 7
从末尾往前看,数字逐渐变大,找到第一个开始变小的数字,也就是2
1 2 7 4 3 1 然后从后面往前找到第一个大于2的数字,也就是3,这里是想说第二个位置2后面的已经全排列完了,可以换成3了
1 3 7 4 2 1 换成三后面的又要重新进行全排列,全排列最后一个是逆序,第一个是顺序,所以只需要将3后面的翻转一下就可以
1 3 1 2 4 7
code:
1 def nextPermutation(self, nums): 2 """ 3 :type nums: List[int] 4 :rtype: void Do not return anything, modify nums in-place instead. 5 """ 6 a = -1 7 for i in range(len(nums)-1,0,-1): 8 if nums[i] > nums[i-1]: 9 a = i-1 10 break 11 if a==-1: 12 return nums.reverse() 13 b = a+1 14 for j in range(len(nums)-1,a,-1): 15 if nums[j]>nums[a]: 16 b = j 17 break 18 nums[a],nums[b] = nums[b],nums[a] 19 i,j = a+1,len(nums)-1 20 while i<j: 21 nums[i],nums[j] = nums[j],nums[i] 22 i += 1 23 j -= 1
33. Search in Rotated Sorted Array【Medium】 返回目录
题目:

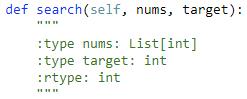
就是说给定的数组是由一个升序数组就某个点翻转得到的,然后要在这样一个数组中查找某个数字,返回下标
解题思路:
直接暴力搜索,O(N) 我以为会超时,结果Accepted 可以没有利用到给定数组的特性,如果是升序数组的话可以用二分法是O(logN), 所以可以设计一个改进版二分法来处理这个问题
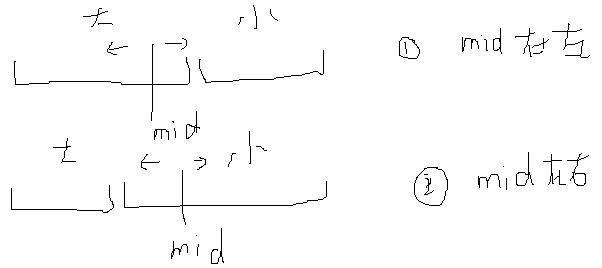
分两种情况:
a)mid如果在左边 : target在mid左 high=mid-1 target在mid右 low=mid+1
b)mid如果在右边 : target在mid左 high=mid-1 target在mid右 low=mid+1
code:(暴力法) beat 16.87%
1 def search(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 for i in range(len(nums)): 8 if nums[i] == target: 9 return i 10 return -1
code:(改进二分法) beat 25.32%
1 def search(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: int 6 """ 7 if len(nums) < 1: 8 return -1 9 low,high = 0, len(nums)-1 10 while(low<high): 11 mid = (low + high) // 2 12 if nums[mid] == target: 13 return mid 14 if nums[low] <= nums[mid]: 15 if target >= nums[low] and target < nums[mid]: 16 high = mid - 1 17 else: 18 low = mid + 1 19 else: 20 if target > nums[mid] and target <= nums[high]: 21 low = mid + 1 22 else: 23 high = mid -1 24 if nums[low] == target: 25 return low 26 else: 27 return -1
34. Search for a Range 【Medium】 返回目录
题目:

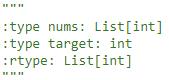
解题思路:
要求在O(logn)时间内,那么就是希望我们用二分法进行查找,首先先用二分法找到相应的值,然后再向左判断边界,再向右判断边界,向左向右的过程中都是使用二分法
code: beat 21.43%
1 def searchRange(self, nums, target): 2 """ 3 :type nums: List[int] 4 :type target: int 5 :rtype: List[int] 6 """ 7 if len(nums) < 1: 8 return [-1,-1] 9 low,high = 0,len(nums)-1 10 if nums[0]>target or nums[-1]<target: 11 return [-1,-1] 12 while(low <= high): 13 mid = (low+high)//2 14 if nums[mid] < target: 15 low = mid + 1 16 elif nums[mid] == target: 17 b = mid 18 high = mid - 1 19 else: 20 high = mid - 1 21 if nums[high+1] != target: 22 return [-1,-1] 23 a = high+1 24 high = len(nums)-1 25 while(low <= high): 26 mid = (low+high)//2 27 if nums[mid] > target: 28 high = mid - 1 29 else: 30 low = mid + 1 31 return [a,low-1]
39. Combination Sum 【Medium】 返回目录
题目:

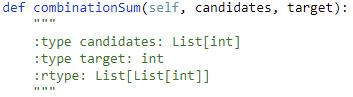
解题思路:
搜索+回溯 这道题很经典,理清楚怎么递归和回溯很重要
主要思路就是先第一个数字,再递归的求target-第一个数字,可以的话继续递归,不可以就回溯
我发现我真是有点笨,经常想不通怎么回溯
dfs的算法一定要非常熟悉,在python中通常都是要把path和result作为参数传入dfs函数中,用以记录可行的结果
Tips:求所有可能的解的时候就要想到搜索和递归
code: 参考的别人写的代码 beat 69.7% (大神就是厉害)
1 def combinationSum(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 self.dfs(candidates,target,0,[],res) 9 return res 10 def dfs(self,nums,target,index,path,res): 11 if target<0: 12 return 13 elif target==0: 14 res.append(path) 15 return 16 else: 17 for i in range(index,len(nums)): 18 self.dfs(nums,target-nums[i],i,path+[nums[i]],res)
上面的是递归回溯,下面是栈回溯
code: beat 68.18%
1 def combinationSum(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 self.dfs(candidates,target,0,[],res) 9 return res 10 def dfs(self,nums,target,index,path,res): 11 if target<0: 12 return 13 elif target==0: 14 res.append(path[:]) 15 return 16 else: 17 for i in range(index,len(nums)): 18 path.append(nums[i]) 19 self.dfs(nums,target-nums[i],i,path,res) 20 path.pop()
而且我今天还对python中的赋值机制进行了深入的学习,起因是第14行代码 如果直接写成 res.append(path)的话,后面修改path是在原地址上修改,起不到保存结果的作用,所以用path[:]切片操作,相当于创建了一个新的对象进行保存,就可以让代码正常运行了
学习链接是: https://my.oschina.net/leejun2005/blog/145911 这个博客解释得相当清楚
40. Combination Sum II 【Medium】 返回目录
题目: 同39 只是要求一个数只能用一次,所以只是循环的时候要求index+1,具体细节看39题
code: beat 73.81%
1 def combinationSum2(self, candidates, target): 2 """ 3 :type candidates: List[int] 4 :type target: int 5 :rtype: List[List[int]] 6 """ 7 res = [] 8 candidates.sort() 9 print(candidates) 10 self.dfs(candidates,target,[],0,res) 11 return res 12 def dfs(self,nums,target,path,index,res): 13 if target<0: 14 return 15 elif target==0: 16 res.append(path) 17 return 18 else: 19 for i in range(index,len(nums)): 20 if i>index and nums[i]==nums[i-1]: 21 continue 22 self.dfs(nums,target-nums[i],path+[nums[i]],i+1,res)
48. Rotate Image 【Medium】 返回目录
题目:
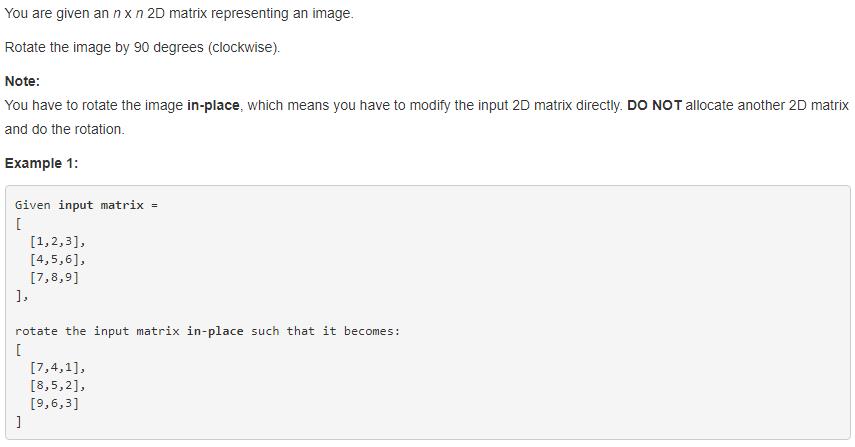

解题思路:
主要是寻找旋转前和旋转后坐标位置的对应关系,我们发现
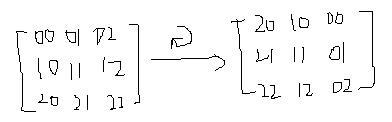
所以就是对每一个正方形框的上边进行逐个元素的旋转置位,就可以了
code: beat 70.69% 完全自己写的,好有成就感哈哈哈~
1 def rotate(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: void Do not return anything, modify matrix in-place instead. 5 """ 6 n = len(matrix)-1 7 for i in range(n//2+1): 8 for j in range(n-2*i): 9 matrix[i][i+j],matrix[i+j][n-i],matrix[n-i][n-i-j],matrix[n-i-j][i] = matrix[n-i-j][i],matrix[i][i+j],matrix[i+j][n-i],matrix[n-i][n-i-j]
然后看了下别人的解法
code: 比我的解法简单太多了,膜拜大神
1 def rotate(self, matrix): 2 """ 3 :type matrix: List[List[int]] 4 :rtype: void Do not return anything, modify matrix in-place instead. 5 """ 6 \'\'\' 7 clockwise rotate 8 以上是关于leetcode解题笔记--part1--array的主要内容,如果未能解决你的问题,请参考以下文章