逻辑回归 算法推导与基于Python的实现详解

Posted 2023-03-26 专注算法的马里奥学长

文章目录

• 1 逻辑回归概述
• 2 逻辑回归公式推导与求解
• • 2.1 公式推导
  • 2.2公式求解
• 3 基于Python的实现
• • 3.1可接收参数
  • 3.2 完整代码示例

1 逻辑回归概述

逻辑回归（Logistic Regression）是一种用于分类问题的统计学习方法。它基于线性回归的原理，通过将线性函数的输出值映射到[0,1]区间上的概率值，从而进行分类。

逻辑回归的输入是一组特征变量，它通过计算每个特征与对应系数的乘积，加上截距项得到线性函数，然后将该函数的输出值经过sigmoid函数的映射，得到概率值。

逻辑回归常用于二分类问题，即将样本分为两类，如判断一封邮件是否为垃圾邮件。逻辑回归还可以扩展到多分类问题，如将样本分为三类或更多类别。

逻辑回归具有简单、高效、易于理解等优点，在实际应用中被广泛使用，如金融风控、医学诊断、推荐系统等领域。

2 逻辑回归公式推导与求解

2.1 公式推导

$$P(y=1|x)=\frac{1}{1+e^{-({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_p{x}_p)}}$$
逻辑回归的公式大家可能很熟悉，但并不知道推导过程，事实上这一推导过程也十分简单。

给定输入特征 $\mathbf{x}$，逻辑回归模型的输出 $y$ 可以表示为：

$$y=P(y=1|\mathbf{x})=\sigma ({\mathbf{w}}^T\mathbf{x})$$

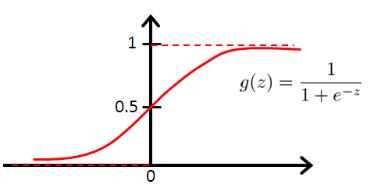
其中，$\sigma (z)$ 表示 sigmoid 函数，定义为：$\sigma (z)=1/(1+e^{-z})$。这一函数在之后的深度学习中也会经常用到。

至于什么使用sigmoid函数，原因也很简单，很多教材都把这个重要的思考环节忽略了，博主在此进行补充。
我们希望找到一个函数的值域在[0，1]的函数，但是这种函数并不容易找到，线性回归使用的公式$y=\theta x$的值域是（-∞，+∞）。因此，我们引入了odds（几率）的概念。$$odds=\frac{P}{1-P}$$odds的取值为(0,+∞)，而对于log函数，其定义域刚好为(0,+∞)，值域为（-∞，+∞）。因此，我们便可以构造一个函数$$\log (\frac{P}{1-P})=\theta x$$对P进行求解，即得到了逻辑回归的基本形式$$P=\frac{1}{1+e^{-x}}$$也就是我们所常说的sigmoid函数。

2.2公式求解

为了方便推导，我们假设训练数据集包含 $m$ 个样本，每个样本有 $n$ 个特征，即 $\mathbf{X}\in {\mathbb{R}}^{m\times n}$，标签为 $y\in 0,1{}^m$。为了构建模型，我们需要使用训练数据集求解模型参数 $\mathbf{w}$。

我们使用最大似然估计来求解模型参数。最大似然估计的目标是找到一组模型参数 $\mathbf{w}$，使得训练数据集出现的概率最大。设训练数据集中的第 $i$ 个样本的输入特征为 ${\mathbf{x}}_i$，输出为 $y_i$，其概率表示为：

$$P(y_i|{\mathbf{x}}_i;\mathbf{w})=\sigma ({\mathbf{w}}^T{\mathbf{x}}_i{)}^{y_i}(1-\sigma ({\mathbf{w}}^T{\mathbf{x}}_i){)}^{1-y_i}$$

训练数据集的概率可以表示为：

$$P(y|\mathbf{X};\mathbf{w})=\prod _{i}P(y_i|{\mathbf{x}}_i;\mathbf{w})=\prod _i\sigma ({\mathbf{w}}^T{\mathbf{x}}_i{)}^{y_i}(1-\sigma ({\mathbf{w}}^T{\mathbf{x}}_i){)}^{1-y_i}$$

对数似然函数为：

$$L(\mathbf{w})=\log P(y|\mathbf{X};\mathbf{w})=\sum _i[y_i\log (\sigma ({\mathbf{w}}^T{\mathbf{x}}_i))+(1-y_i)\log (1-\sigma ({\mathbf{w}}^T{\mathbf{x}}_i))]$$

我们的目标是最大化对数似然函数 $L(\mathbf{w})$。使用梯度上升算法来求解最优参数 $\mathbf{w}$。对 $L(\mathbf{w})$ 求导，得到： ∂ L ( w ) ∂ w = ∑ i ( σ ( w T x i ) − y i ) x i \\frac\\partial L(\\mathbfw)\\partial \\mathbfw = \\sum_i(\\sigma(\\mathbfw^T \\mathbfx_i) - y_i)\\mathbfx_i ∂w∂L(w)​=逻辑回归LR算法LR优缺点LR推导LR损失函数

局部加权之逻辑回归 - Python实现

详解线性分类-逻辑回归（Logistic Regression）白板推导系列笔记

逻辑回归模型 Logistic Regression 详细推导 (含 Numpy 与PyTorch 实现)

西瓜书经典算法推导对数几率回归（逻辑回归）

机器学习算法面试为什么逻辑回归的损失函数是交叉熵？