Python实现Vgg16经典网络架构代码
Posted quintin007
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python实现Vgg16经典网络架构代码相关的知识,希望对你有一定的参考价值。
Python实现Vgg16经典网络架构代码
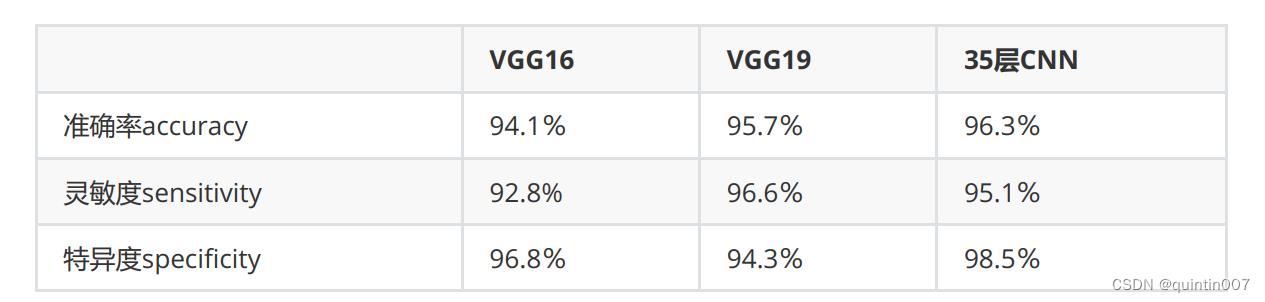
可以看到,从16层到19层,准确率上升了1.6%,但从19层到35层,准确率却只上升了0.6%。不难发现
——16层明显比13层要高,但19层却和16层差异不太大,35层与19层之间的差异就更小,随着深度的
加深,模型的学习能力大概率会增强,但深度与模型效果之间的关系不是线性的,可以增长的边际准确
率是在递减的,准确率的变化会逐渐趋于平缓。但同时,参数量却是高速增加的,VGG19的参数量就达
到了1.43亿个,对于任何个人计算机来说这个参数量都是一个巨大的考验。
受启发于VGG架构,在过去数年的研究中,人们通过实验发现了这样的结论:在不改变原始卷积层输入
输出机制的前提下,增加卷积层的数目来增加深度,会很快让模型效果和性能都达到上限。深度并不能
高效提升模型的效果,需要先降低模型的训练成本,才能够追求更深的神经网络。如果想要通过“加深”
卷积神经网络来实现网络效果的飞跃,那必须是从16层加到160层,而不是从16层加到19层。事实上,
在2014年后的ILSVRC上,赢得冠军的网络架构变得越来越复杂,深度也越来越深,在2017年ILSVRC闭
幕之前,网络深度大约停留在了220层左右,这是得益于研究者们发现了更高效地提升深度的方法。
在现在的眼光来看,网络的实际深度一般与数据的复杂程度有关。对于ImageNet这样的数据集,200层
的网络能够实现2.99%的错误率,而对于Fashion-MNIST这样的数据集,可能只需要几十层就能达到很
高的测试准确率(目前为止Github上的Fashion-MNIST最高测试准确率大约在96%)。对于尺寸小于
50x50的图像而言,若追求测试准确率在90%以上,则只需要小于20层左右就足够了。为了计算效率,
不必强行加深网络,若的确追求更高的准确率,则可以考虑换成更高级的架构或者对数据进行预处理。
VGG架构对于神经网络研究和使用都有重要的意义,它不仅简单、有效,而且非常适合用来做各种实验
和测试。在我们已经详细复现AlexNet与LeNet5的基础上,VGG架构的代码就显得异常简单。在这里,
我为大家提供输入为224x224的VGGNet16的详细架构和复现后的代码,大家可以参考。VGG16的架构
用语言来表示则有:
输入→(卷积x2+池化)x2 →(卷积x3+池化)x3 → FC层x3 →输出。
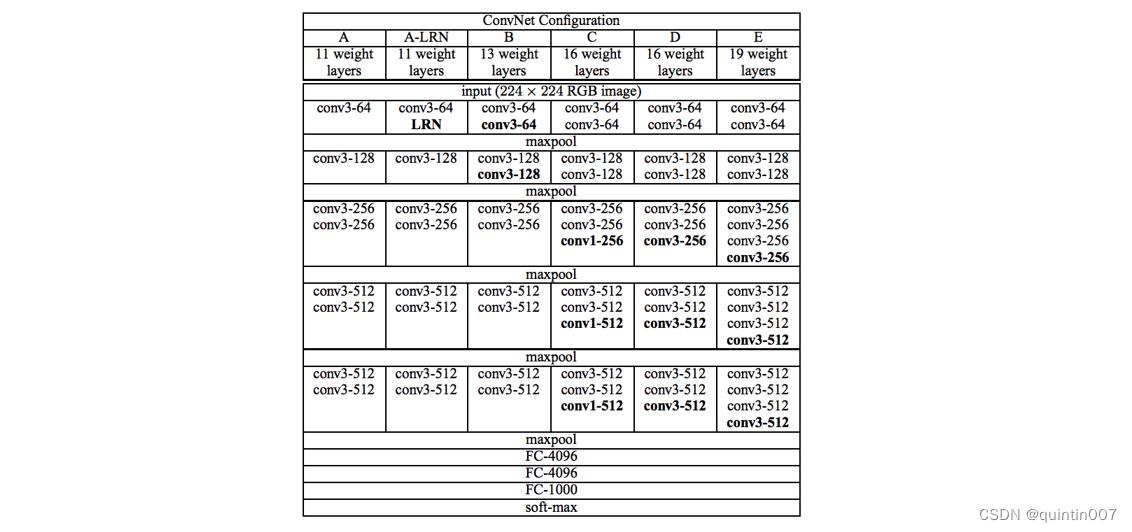
实现代码如下:
import torch
import torch.nn as nn
from torchinfo import summary
from torch.nn import functional as F
data=torch.ones(10,3,224,224)
class Vgg16(nn.Module):
def __init__(self):
super().__init__()
self.conv1=nn.Sequential(nn.Conv2d(3,64,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(64,64,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(kernel_size=2))
self.conv2=nn.Sequential(nn.Conv2d(64,128,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(128,128,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(kernel_size=2))
self.conv3=nn.Sequential(nn.Conv2d(128,256,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(256,256,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(256,256,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(kernel_size=2))
self.conv4=nn.Sequential(nn.Conv2d(256,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(512,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(512,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(kernel_size=2))
self.conv5=nn.Sequential(nn.Conv2d(512,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(512,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.Conv2d(512,512,kernel_size=3,padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(kernel_size=2))
self.fc=nn.Sequential(nn.Linear(7*7*512,4096)
,nn.ReLU(inplace=True)
,nn.Linear(4096,4096)
,nn.ReLU(inplace=True)
,nn.Linear(4096,1000)
,nn.ReLU(inplace=True)
)
def forward(self,x):
x=self.conv1(x)
x=self.conv2(x)
x=self.conv3(x)
x=self.conv4(x)
x=self.conv5(x)
x=torch.flatten(x,1)
x=self.fc(F.dropout( x,0.5))
out =F.softmax(x)
return out
vgg_=Vgg16()
vgg_(data)
<ipython-input-25-17853c1700ab>:50: UserWarning: Implicit dimension choice for softmax has been deprecated. Change the call to include dim=X as an argument.
out =F.softmax(x)
tensor([[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010],
[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010],
[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010],
...,
[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010],
[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010],
[0.0010, 0.0010, 0.0010, ..., 0.0010, 0.0010, 0.0010]],
grad_fn=<SoftmaxBackward0>)
summary(vgg_,data.shape,depth=3)
<ipython-input-25-17853c1700ab>:50: UserWarning: Implicit dimension choice for softmax has been deprecated. Change the call to include dim=X as an argument.
out =F.softmax(x)
==========================================================================================
Layer (type:depth-idx) Output Shape Param #
==========================================================================================
Vgg16 [10, 1000] --
├─Sequential: 1-1 [10, 64, 112, 112] --
│ └─Conv2d: 2-1 [10, 64, 224, 224] 1,792
│ └─ReLU: 2-2 [10, 64, 224, 224] --
│ └─Conv2d: 2-3 [10, 64, 224, 224] 36,928
│ └─ReLU: 2-4 [10, 64, 224, 224] --
│ └─MaxPool2d: 2-5 [10, 64, 112, 112] --
├─Sequential: 1-2 [10, 128, 56, 56] --
│ └─Conv2d: 2-6 [10, 128, 112, 112] 73,856
│ └─ReLU: 2-7 [10, 128, 112, 112] --
│ └─Conv2d: 2-8 [10, 128, 112, 112] 147,584
│ └─ReLU: 2-9 [10, 128, 112, 112] --
│ └─MaxPool2d: 2-10 [10, 128, 56, 56] --
├─Sequential: 1-3 [10, 256, 28, 28] --
│ └─Conv2d: 2-11 [10, 256, 56, 56] 295,168
│ └─ReLU: 2-12 [10, 256, 56, 56] --
│ └─Conv2d: 2-13 [10, 256, 56, 56] 590,080
│ └─ReLU: 2-14 [10, 256, 56, 56] --
│ └─Conv2d: 2-15 [10, 256, 56, 56] 590,080
│ └─ReLU: 2-16 [10, 256, 56, 56] --
│ └─MaxPool2d: 2-17 [10, 256, 28, 28] --
├─Sequential: 1-4 [10, 512, 14, 14] --
│ └─Conv2d: 2-18 [10, 512, 28, 28] 1,180,160
│ └─ReLU: 2-19 [10, 512, 28, 28] --
│ └─Conv2d: 2-20 [10, 512, 28, 28] 2,359,808
│ └─ReLU: 2-21 [10, 512, 28, 28] --
│ └─Conv2d: 2-22 [10, 512, 28, 28] 2,359,808
│ └─ReLU: 2-23 [10, 512, 28, 28] --
│ └─MaxPool2d: 2-24 [10, 512, 14, 14] --
├─Sequential: 1-5 [10, 512, 7, 7] --
│ └─Conv2d: 2-25 [10, 512, 14, 14] 2,359,808
│ └─ReLU: 2-26 [10, 512, 14, 14] --
│ └─Conv2d: 2-27 [10, 512, 14, 14] 2,359,808
│ └─ReLU: 2-28 [10, 512, 14, 14] --
│ └─Conv2d: 2-29 [10, 512, 14, 14] 2,359,808
│ └─ReLU: 2-30 [10, 512, 14, 14] --
│ └─MaxPool2d: 2-31 [10, 512, 7, 7] --
├─Sequential: 1-6 [10, 1000] --
│ └─Linear: 2-32 [10, 4096] 102,764,544
│ └─ReLU: 2-33 [10, 4096] --
│ └─Linear: 2-34 [10, 4096] 16,781,312
│ └─ReLU: 2-35 [10, 4096] --
│ └─Linear: 2-36 [10, 1000] 4,097,000
│ └─ReLU: 2-37 [10, 1000] --
==========================================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
Total mult-adds (G): 154.84
==========================================================================================
Input size (MB): 6.02
Forward/backward pass size (MB): 1084.54
Params size (MB): 553.43
Estimated Total Size (MB): 1643.99
==========================================================================================
以上是关于Python实现Vgg16经典网络架构代码的主要内容,如果未能解决你的问题,请参考以下文章