机器学习｜逻辑回归｜吴恩达学习笔记 | 牛顿法

Posted 2023-03-21 啦啦右一

前文回顾：多变量线性回归

---

分类问题举例：

• 判断一封电子邮件是否是垃圾文件
• 判断一次金融交易是否是欺诈
• 区分肿瘤是恶性的还是良性的

在分类问题中，我们尝试预测的是结果是否属于某一个类（例如正确或错误），即我们要预测的变量y是离散的值，这里要用到的是逻辑回归算法。它的性质是：它的输出值永远在0到1之间。

📚假说表示

对于以下的乳腺癌分类问题，我们可以用线性回归的方法求出适合数据的一条直线：

根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

• 当h(x) ≥ 0.5时，预测y = 1
• 当h(x) ≤ 0.5时，预测y = 0

对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。但假使我们又观测到了一个非常大的尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

这时，再使用0.5作为阈值来预测肿瘤是良性还是恶性就不合适了（会有恶性肿瘤被误认为是良性肿瘤）。

---

我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。

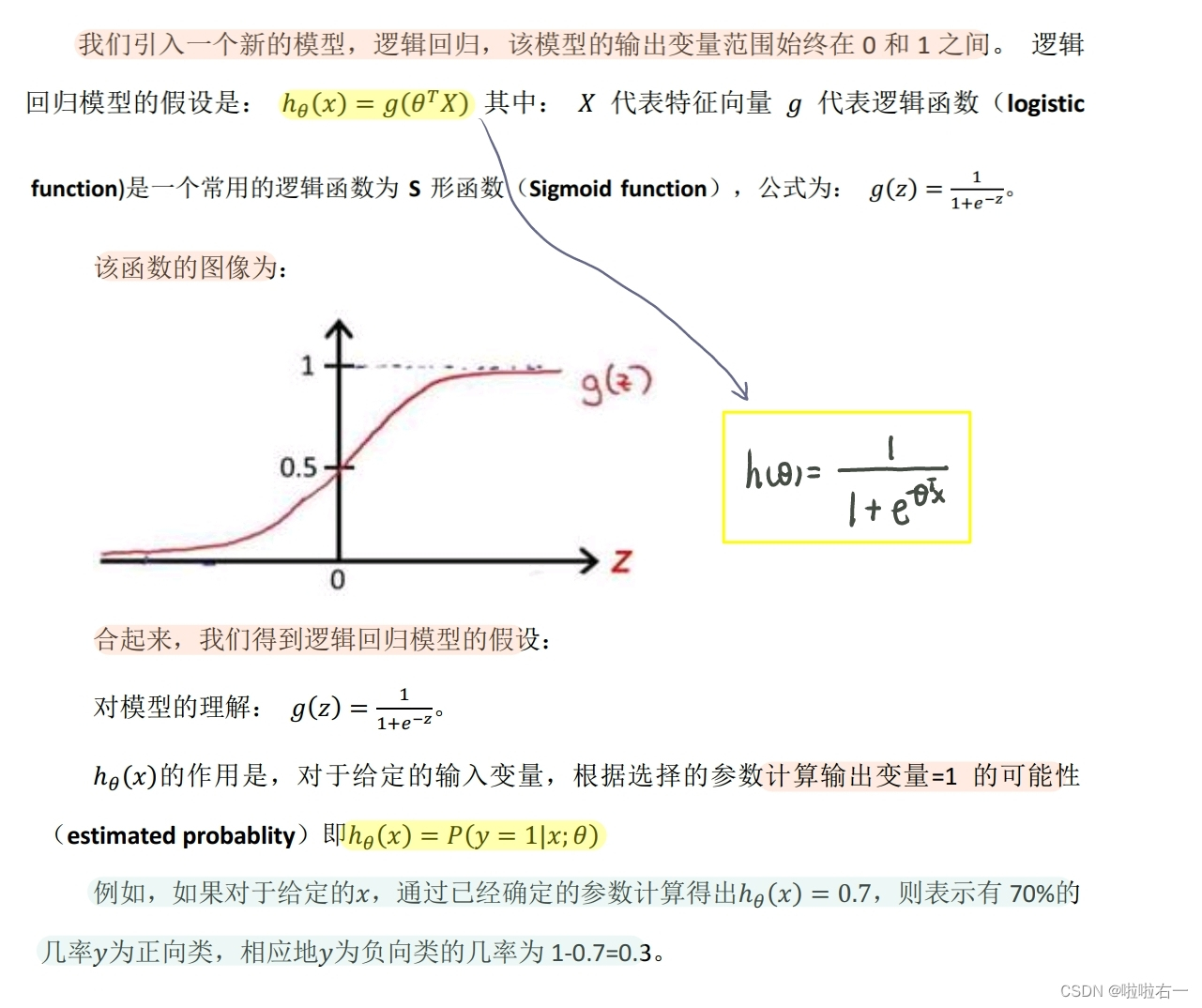
借助于Sigmoid function，预测函数被很好地限制在[0,1]之间。

• 当 z 趋向于 +∞ 时，g(z)趋向于1
• 当 z 趋向于 -∞ 时，g(z)趋向于0
• 

我们假设的输出，实际上就是这个概率值：p(y = 1 | x ; θ)，就是关于x以θ为参数，y = 1的概率。

• 

---

 📚判定边界

判定边界，就是用来划定界限的边界。

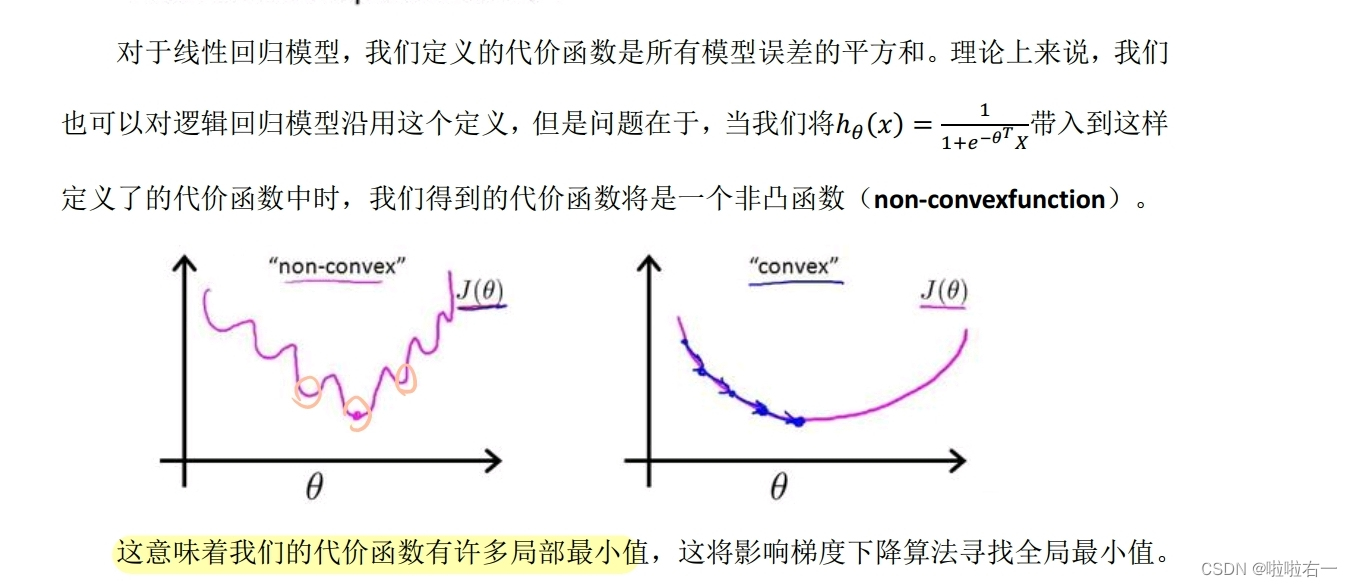
  📚代价函数

 

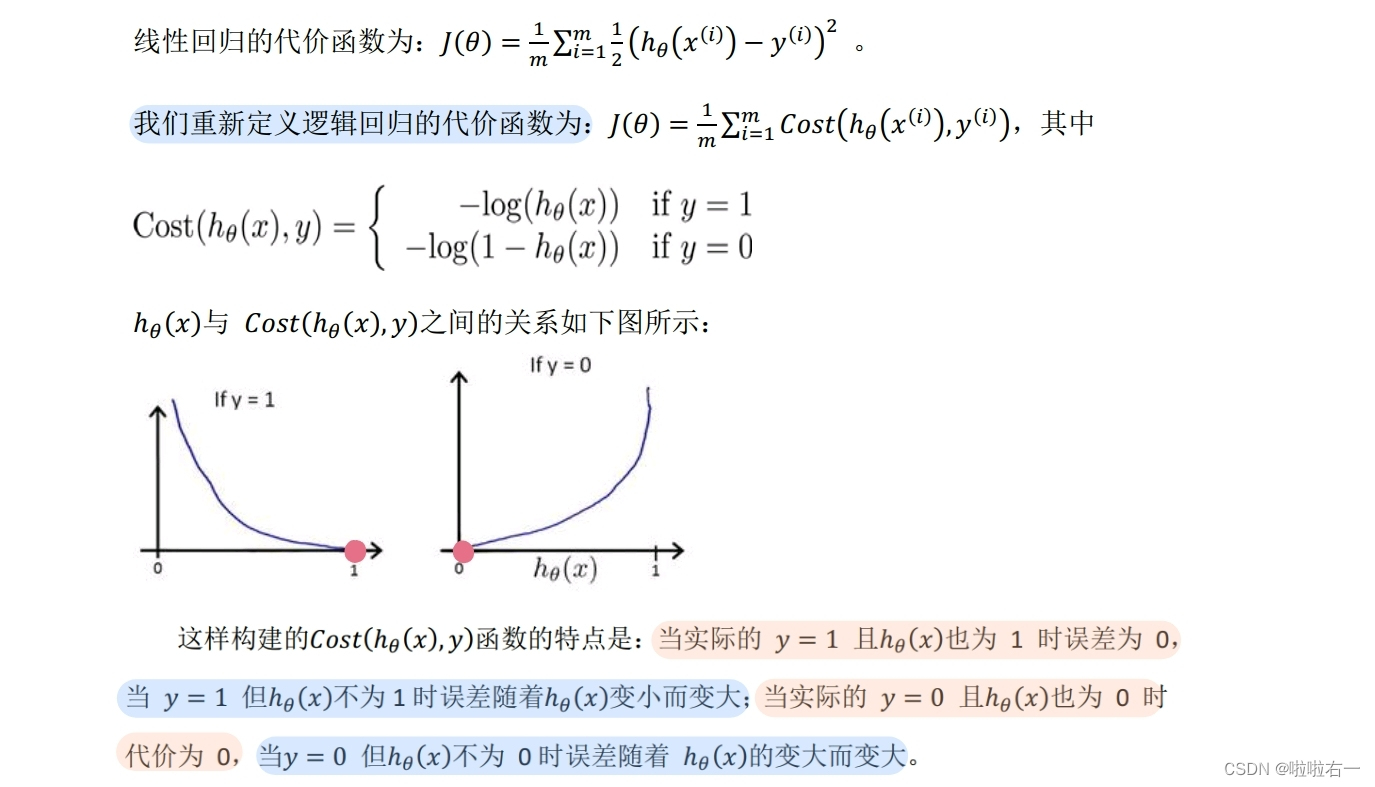
📚简化的成本函数和梯度下降

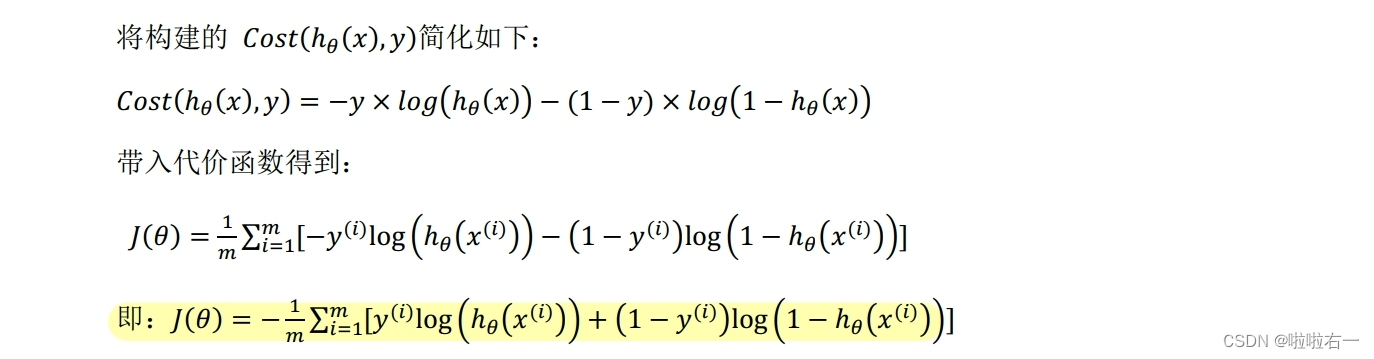
根据这个代价函数，为了拟合参数，我们要试图找尽量让J(θ)取得最小值的参数θ（这一点和线性回归是一样的，就是找代价最少的对应情况）。针对所给出的一个新的样本，假如某个特征x，我们可以用拟合训练样本的参数θ，来输出对假设的预测。

---

我们假设的输出，实际上就是这个概率值：p(y = 1 | x ; θ)，就是关于x以θ为参数，y = 1的概率。可以说，我们的假设就是估计y = 1的概率。

---

最小化代价函数的方法，在这里还是用梯度下降法。

模式上看，这个更新规则和我们之前用在线性回归上的是一样的。但因为线性回归的h(θ)和逻辑回归的h(θ)不同，所以它们的梯度下降，实际上是完全不同的。

---

当使用梯度下降法来实现逻辑回归时，我们有这些不同的参数θ，我们需要用这个表达式来更新这些参数。理想情况下使用向量化来实现，可以把所有这些n个参数同时更新。除此之外，特征缩放同样也适合于逻辑回归。

📚高级优化

• 共轭梯度(Conjugate Gradient)
• 局部优化法(Broyden fletcher goldfarb shann,BFGS)
• 有限内存局部优化法(LBFGS)

对于6.6中提到的优化算法，我们通常不需要手动选择学习率a，对于这些算法的思路是，给出计算导数项和代价函数的方法。可以认为算法有一个智能的内部循环（事实上确实有一个智能的内部循环，称为线性搜索，它可以自己尝试不同的学习速率a，并自动选择一个好的学习速率a，甚至可以为每次迭代选择不同的学习速率，总之就是不需要我们来选择）。这些算法实际上在做更复杂的事情，它们往往最终收敛得远远快于梯度下降。

建议使用函数库fminunc

📚多类别分类：一对多

总得来说，就是把一个多分类问题转化成多次二分类问题。在二分类中，我们把数据集分为正类和负类，在一对多问题中就是依次把某一类看作正类把其他的看作是负类，分别求出对应的h(θ)，最后针对新数据x的预测，分别代入对应的h(θ)，取其中的最大值。

---

 以上参考学习链接：【中英字幕】吴恩达机器学习系列课程，本篇对应6.1-6.7

---

📚拓展补充

🐇最大似然估计拟合参数

🐇梯度下降公式推导

🐇牛顿法

梯度下降是用梯度来建立迭代关系式的方法，而牛顿法是用切线来建立迭代关系式的算法。牛顿法的迭代过程与梯度下降有相似之处，只不过用切线和x轴的交点来作为下一轮迭代的起点。

牛顿法有两个应用方向：求解方程根的问题和目标函数最优化求解问题。牛顿法的本质是泰勒展开。

---

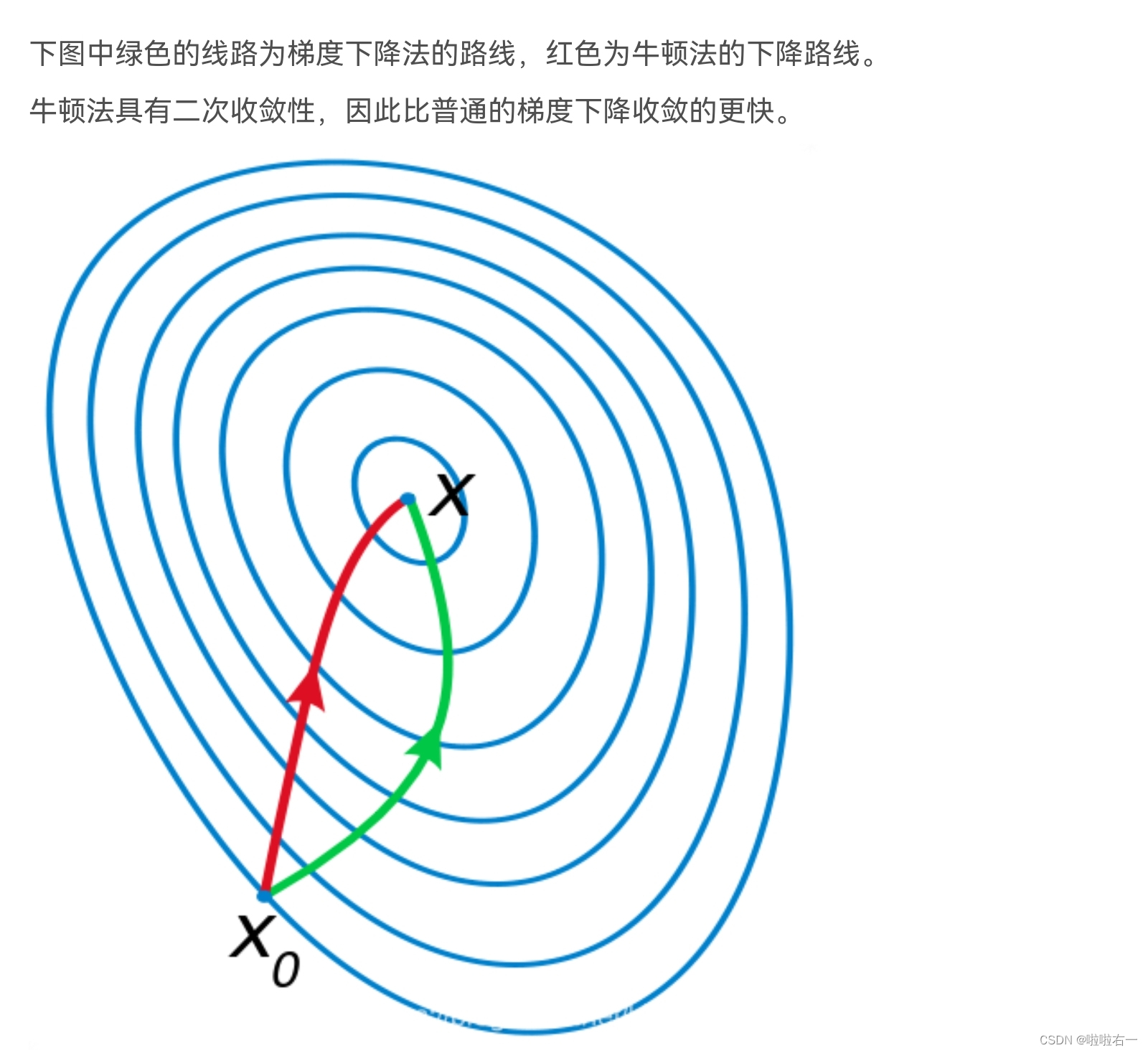
牛顿法的精髓就是二阶收敛，不仅利用了损失函数的一阶偏导数，也用到了损失函数的二阶偏导数，即梯度变化的趋势，因此比梯度下降法更快地确定合适的搜索方向，具有二阶收敛速度。通俗点来说，梯度下降法时选择下一步能迈出的最大步长，而牛顿法是在选择下一步能迈出的最大步长的基础上，同时也考虑了下下步的选择方向。也就是牛顿法更加具有大局观。

---

参考博客

牛顿法及其几何意义理解

机器学习——牛顿法详解