计算机二进制，十进制，八进制，十六进制怎么转换

Posted 2023-03-20

谁可以告诉我，计算机，十进制，八进制，十进制，十六进制到底怎么转换啊！老师讲的太烦了，我搞不清楚怎么转换，哪位有什么技巧吗？好着急啊！

1、二进制转换为十进制

二进制数00111从低位到高位的位权依次是2的0次幂1、2的1次幂2、2的2次幂4、2的3次幂8、2的4次幂16。

理解了二进制计数的基数和位权，就可以进行数制转换了。00111如何转换成十进制计数呢？转换很简单，将二进制数从高位到低位每个数字乘以相应的位权然后求和就可以了。

00111（二进制）= 0 * 2^(5-1) + 0 * 2^(4-1) + 1 * 2^(3-1) + 1 * 2^(2-1) + 1 * 2^(1-1)

= 0 * 16 + 0 * 8 + 1 * 4 + 1 * 2 + 1 * 1

= 7（十进制）

2、十进制转换为二进制

十进制整数到二进制整数的转换可以采用“除2取余，逆序输出”法，

具体转换过程是，用2去除一个十进制数，得到商和余数，然后再用2去除商，又会得到商和余数，循环往复直至商为0为止。如果是十进制小数转二进制小数，则采用“乘2取整，顺序输出”。转换过程如下图所示：

3、二进制和八进制之间的转换

二进制转八进制：取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。

如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位。

4、八进制转二进制：取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧。

5、二进制和十六进制之间的转换

二进制转十六进制：取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数。

如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位。

6、十六进制转二进制：取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧。

7、十进制和八进制之间、十进制和十六进制之间都是先把十进制转换为二进制，然后在转换为八进制或者十六进制。

扩展资料

某进制计数制允许选用的基本数字符号的个数成为基数。一般来说，N进制的基数为N，可进行选用的基本数字符号有N个，分别为0到N-1。

比如十六进制的基数为16，可供选择的基本数学符号为0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F十六个。

位权是指，该进位制中每一固定位置对应的单位值，简称为权。

以十进制计数制来说，计数单位分别为个位、十位、百位、千位、万位、十万位……，其中个位数表示数值1、十位数表示数值10、百位数表示数值100、千位数表示数值1000、……，每个位数表示的数值叫位权。

位权通过计算基数的n-1次幂就可以得到，这里的n是指位数所在数字中的位置。在十进制中就是10的(n-1)次幂。

例如，对十进制数1260来说，个位数是1260的第一个数字，因此n为1；十位数是第二个数字，因此n为2；百位数是第三个数字，因此n为3；千位数是第四个数字，因此n为4。

由此，个位数的位权为10的1-1次幂是1，十位数的位权为10的2-1次幂是10、百位数的位权为10的3-1次幂是100、千位数的位权为10的4-1次幂是1000。

1260 = 1 * 10^(4-1) + 2 * 10^(3-1) + 6 * 10^(2-1) + 0 * 10^(1-1)

= 1 * 1000 + 2 * 100 + 6 * 10 + 0 * 1

= 1000 + 200 + 60 + 0

参考资料来源：百度百科-进制

参考技术A

1.什么是二进制

二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”，由18世纪德国数理哲学大师莱布尼兹发现。当前的计算机系统使用的基本上是二进制系统，数据在计算机中主要是以补码的形式存储的。计算机中的二进制则是一个非常微小的开关，用“开”来表示1，“关”来表示0。       

.信息的存储单位

位(Bit) :度量数据的最小单位

字节(Byte):最常用的基本单位，一个字节有8位

b7  b6 b5 b4 b3 b2 b1 b0

1    0   0  1   0   1   0   1  =27+24+22+20=149

K字节       1k=1024 byte

M(兆)字节  1M=1024K

G(吉)字节  1G=1024M

T(太)字节  1T=1024G

2.十进制转换

1234[10进制] 0 1 2 3 4 5 6 7 8 9 0 当数位上的值超过9就要进1

1000+200+30+4=1*103+2*102+3*101+4*100=1234

1011[2进制] 0 1 当数位上的值超过1就要进1

1*23+0*22+1*21+1*20=8+0+2+1=11

1011[8进制]0 1 2 3 4 5 6 7 当数位上的值超过7就要进1

1*83+1*81+1*80=512+8+1=521

1011[16进制]0 1 2 3 4 5 6 7 8 9 A B C D E F 当数位上的值超过15就要进1

1*163+1*161+1*160=4096+16+1=4113

3.二进制转换

首先来看十进制到二进制:除2取余数 最后把余数倒过来 100101

比如：十进制数37

所以转换成的二进制数字为:100101

再来八进制到二进制：一个八进制的位拆分成一个三位的二进制数

比如：[八进制]616

6拆分成 110

1拆分成 001

6拆分成 110

所以转换成的二进制数字为:110001110

再来十六进制到二进制：一个八进制的位拆分成一个四位的二进制数

比如：[十六进制]616

6拆分成 0110

1拆分成 0001

6拆分成 0110

所以转换成的二进制数字为:11000010110

4.八进制转换

十进制到八进制：除8取余数 最后把余数倒过来

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成八进制 

比如:2456 转化成八进制数字：4630

2456/8=307，余0；
307/8=38，余3；
38/8=4，余6；
4/8=0，余4。
将所有余数倒序相连，得到结果：4630。
因此十进制的2456转换为八进制结果为4630。

二进制到八进制转换  7=4+2+1 111 八进制最大的数字是7转换成二进制刚好是111，占3个位

每三个二进制数为一组，转成一个八进制数位，如果二进制高位不足3位时，用零填补。

比如：10011011

010 011 011

2     3     3

因此二进制的10011011转换为八进制结果为233。

5. 十六进制到八进制

我们可以先把十六进制的数字转换成二进制，在从二进制转换成八进制例如： 

3BC24 
分别对应到二进制就是： 
3 0011 
B 1011 
C 1100 
4 0100

连起来就是： 
0011 1011 1100 0100

再按照每三个一组分组： 
0 011 101 111 000 100

0__3__5__7__0__4 
所以8进制就是35704

6.十六进制转换

十进制到十六进制：除16倒着取余数

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成十六进制 

比如说：1610转换成十六进制

直接转16进制：
1610/16=100……10(A)；
100 /16= 6……4；
6 /16= 0……6；

故：1610(10)=64A(16).

二进制到十六进制 15=8+4+2+1   1111 十六进制最大数字是F,即15转换成二进制1111，刚好占4个位

每四个二进制数为一组，转成一个十六进制数位，如果二进制高位不足3位时，用零填补。

比如：1110011011

0011 1001 1011

3       9      B

因此二进制的 1110011011转换为十六进制39B

八进制到十六进制

我们可以先把八进制的数字转换成二进制，在从二进制转换成十六进制

八进制的：1234567

转换为二进制是每个数字转换为三位二进制：001 010 011 100 101 110 111

然后把这些数字从右边开始进行按四位分组：0 0101 0011 1001 0111 0111

然后从右边每四位组依次对应一个16进制数：053977

7.各种进制的用途

说了这么多，这些进制都有些什么用了，大家一起讨论下吧！！！

10进制，当然是便于我们人类来使用，我们从小的习惯就是使用十进制，这个毋庸置疑。

2进制，是供计算机使用的，1，0代表开和关，有和无，机器只认识2进制。

16进制，内存地址空间是用16进制的数据表示, 如0x8049324。

编程中，我们常用的还是10进制。 　　

比如：int a = 100,b = 99; 　　

不过，由于数据在计算机中的表示，最终以二进制的形式存在，所以有时候使用二进制，可以更直观地解决 问题。但二进制数太长了。比如int 类型占用4个字节，32位。比如100，用int类型的二进制数表达将是： 　　

0000 0000 0000 0000 0110 0100 　　

面对这么长的数进行思考或操作，没有人会喜欢。因此，用16进制或8进制可以解决这个问题。因为，进制越大，数的表达长度也就越短。

1.用于计算机领域的一种重要的数制 　　

2.对计算机理论的描述，计算机硬件电路的设计都是很有益的。比如逻辑电路设计中，既要考虑功能的完备，还要考虑用尽可能少的硬件，十六进制就能起到一些理论分析的作用。比如四位二进制电路，最多就是十六种状态，也就是一种十六进制形式，只有这十六种状态都被用上了或者尽可能多的被用上，硬件资源才发挥了尽可能大的作用。 　　

3.十六进制更简短，因为换算的时候一位16进制数可以顶4位2进制数。

8进制，一般有什么用，查了下资料，还真不知道？有知道的大神告诉我吧。

如果你用过linux你可能见过这样表示一个文件的权限：0777、0666等等
可能有的这样解释：具有读权限加1，具有写权限加2，具有执行权限加4，最后的和就是一个角色所具有的权限。而linux有三种角色：属主、属组、其他用户，所以用0777、0666之类的表示。
如果用二进制来看的话，linux用3个bit来表示权限，如果具有某个权限就把那位置1.比如只具有读权限就是100，只具有写权限就是010，具有读写权限就是110，具有读写执行权限就是111。

参考技术B 将负数转换为二进制
比如，假设有一 int 类型的数，值为5，那么，我们知道它在计算机中表示为：
00000000 00000000 00000000 00000101
5转换成二制是101，不过int类型的数占用4字节（32位），所以前面填了一堆0。
现在想知道，-5在计算机中如何表示？
在计算机中，负数以其正值的补码形式表达。
什么叫补码呢？这得从原码，反码说起。
原码：一个整数，按照绝对值大小转换成的二进制数，称为原码。
比如 00000000 00000000 00000000 00000101 是 5的 原码。
反码：将二进制数按位取反，所得的新二进制数称为原二进制数的反码。
取反操作指：原为1，得0；原为0，得1。（1变0; 0变1）
比如：将00000000 00000000 00000000 00000101每一位取反，得11111111 11111111 11111111 11111010。
称：11111111 11111111 11111111 11111010 是 00000000 00000000 00000000 00000101 的反码。
反码是相互的，所以也可称：
11111111 11111111 11111111 11111010 和 00000000 00000000 00000000 00000101 互为反码。
补码：反码加1称为补码。
也就是说，要得到一个数的补码，先得到反码，然后将反码加上1，所得数称为补码。
比如：00000000 00000000 00000000 00000101 的反码是：11111111 11111111 11111111 11111010。
那么，补码为：
11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011
所以，-5 在计算机中表达为：11111111 11111111 11111111 11111011。转换为十六进制：0xFFFFFFFB。
再举一例，我们来看整数-1在计算机中如何表示。
假设这也是一个int类型，那么：
1、先取1的原码：00000000 00000000 00000000 00000001
2、得反码： 11111111 11111111 11111111 11111110
3、得补码： 11111111 11111111 11111111 11111111
可见，－1在计算机里用二进制表达就是全1。16进制为：0xFFFFFF

一个字节等于8位，二进制8位最大的数11111111,而11111111用十进制表示就是255.所以1个字节可以表达的最大的数是255，也就是说表示
0~255这256个数
Java中的移位，如果是short，char，byte的话，都会转换成int的形式再进行移位的。
byte a = 27;// 转换成int为 00000000 00000000 00000000 00011011
byte b = -1;// 转换成int为 11111111 11111111 11111111 11111111
int g = a >> 1;// 有符号右移1位，左侧缺的位以符号位补齐，正数就是0，"00000000 00000000 00000000 00001101" = 13
int f = b >> 1;// 有符号右移1位，左侧缺的位以符号位补齐，负数就是1，"11111111 11111111 11111111 11111111"= -1
故此时打印出来，g=13，gf=-1。
g = a >>> 1;// 无符号右移1位，左侧缺的位以0补齐，"00000000 00000000 00000000 00001101" = 13
f = b >>> 1;// 无符号右移1位，左侧缺的位以0补齐，"01111111 11111111 11111111 11111111" = 2147483647
故此时打印出来，g=13，gf=2147483647。
101111101011110000011111111
f = b << 1;// 无符号左移1位，右侧缺的位以0补齐，"10000000 00000000 00000000 00000010" = -2
故此时打印出来，f= -2
在Thinking in Java第三章中的一段话:

移位运算符面向的运算对象也是
二进制的“位”。可单独用它们处理整数类型（主类型的一种）。左移位运算符（<<）能将运算符左边的运算对象向左移动运算符右侧指定的位数（在低位补0）。 “有符号”右移位运算符（>>）则将运算符左边的运算对象向右移动运算符右侧指定的位数。“有符号”右移位运算符使用了“符号扩展”：若值为正，则在高位插入0；若值为负，则在高位插入1。Java也添加了一种“无符号”右移位运算符（>>>），它使用了“零扩展”：无论正负，都在高位插入0。这一运算符是C或C++没有的。
若对char，byte或者short进行移位处理，那么在移位进行之前，它们会自动转换成一个int。只有右侧的5个低位才会用到。这样可防止我们在一个int数里移动不切实际的位数。若对一个long值进行处理，最后得到的结果也是long。此时只会用到右侧的6个低位，防止移动超过long值里现成的位数。但在进行“无符号”右移位时，也可能遇到一个问题。若对byte或 short值进行右移位运算，得到的可能不是正确的结果（Java 1.0和Java 1.1特别突出）。它们会自动转换成int类型，并进行右移位。但“零扩展”不会发生，所以在那些情况下会得到-1的结果。
1111111111111111111111111111111111111111111111111111111111111111
1011100110000100111111100010101011000111000111000111000111000111 参考技术C 这个有个简便方法就是打开电脑开始附件的计算器,查看改成科学型就可以轻松的转换了 参考技术D

十进制转换：

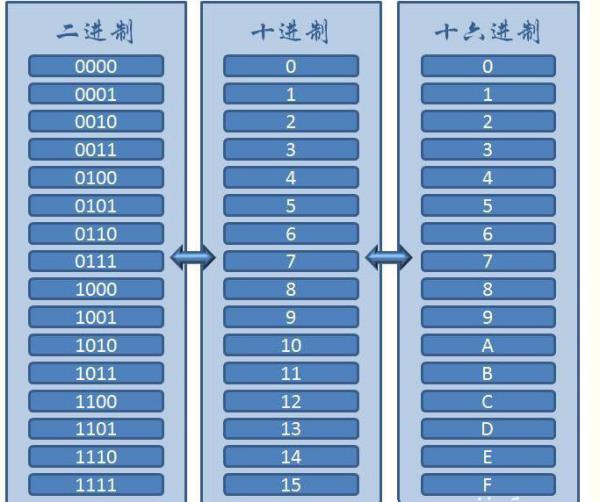
1234[10进制] 0 1 2 3 4 5 6 7 8 9 0 当数位上的值超过9就要进1

1000+200+30+4=1*103+2*102+3*101+4*100=1234。

21011[2进制] 0 1 当数位上的值超过1就要进1

1*23+0*22+1*21+1*20=8+0+2+1=11。

1011[8进制]0 1 2 3 4 5 6 7 当数位上的值超过7就要进1

1*83+1*81+1*80=512+8+1=521。

1011[16进制]0 1 2 3 4 5 6 7 8 9 A B C D E F 当数位上的值超过15就要进1

1*163+1*161+1*160=4096+16+1=4113。

二进制转换：

1、十进制到二进制:除2取余数 最后把余数倒过来 100101

比如：十进制数37

所以转换成的二进制数字为:100101

2、八进制到二进制：一个八进制的位拆分成一个三位的二进制数

比如：[八进制]616

6拆分成 110

1拆分成 001

6拆分成 110

所以转换成的二进制数字为:110001110

3、十六进制到二进制：一个八进制的位拆分成一个四位的二进制数

比如：[十六进制]616

6拆分成 0110

1拆分成 0001

6拆分成 0110

所以转换成的二进制数字为:11000010110

八进制转换：

1、十进制到八进制：除8取余数 最后把余数倒过来

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成八进制 

比如:2456 转化成八进制数字：4630

2456/8=307，余0；
307/8=38，余3；
38/8=4，余6；
4/8=0，余4。
将所有余数倒序相连，得到结果：4630。
因此十进制的2456转换为八进制结果为4630。

2、二进制到八进制转换  7=4+2+1 111 八进制最大的数字是7转换成二进制刚好是111，占3个位

每三个二进制数为一组，转成一个八进制数位，如果二进制高位不足3位时，用零填补。

比如：10011011

010 011 011

2     3     3

因此二进制的10011011转换为八进制结果为233。

十六进制转换：

1、十进制到十六进制：除16倒着取余数

同时我们也可以先将十进制转换成二进制，然后将二进制又转换成十六进制 

比如说：1610转换成十六进制

直接转16进制：
1610/16=100??10(A)；
100 /16= 6??4；
6 /16= 0??6；

故：1610(10)=64A(16).

2、二进制到十六进制 15=8+4+2+1   1111 十六进制最大数字是F,即15转换成二进制1111，刚好占4个位

每四个二进制数为一组，转成一个十六进制数位，如果二进制高位不足3位时，用零填补。

比如：1110011011

0011 1001 1011

3       9      B

因此二进制的 1110011011转换为十六进制39B

拓展资料：

2进制，是供计算机使用的，1，0代表开和关，有和无，机器只认识2进制。

10进制，当然是便于我们人类来使用，我们从小的习惯就是使用十进制，这个毋庸置疑。

16进制，内存地址空间是用16进制的数据表示, 如0x8049324。

编程中，我们常用的还是10进制。 　　

比如：int a = 100,b = 99; 　　

不过，由于数据在计算机中的表示，最终以二进制的形式存在，所以有时候使用二进制，可以更直观地解决 问题。但二进制数太长了。比如int 类型占用4个字节，32位。比如100，用int类型的二进制数表达将是： 　　

0000 0000 0000 0000 0110 0100 　　

面对这么长的数进行思考或操作，没有人会喜欢。因此，用16进制或8进制可以解决这个问题。因为，进制越大，数的表达长度也就越短。

参考资料：

百度百科--二进制